Deep Q-Learning with Space Invaders
Unit 3, of the Deep Reinforcement Learning Class with Hugging Face 🤗
⚠️ A new updated version of this article is available here 👉 https://huggingface.co/deep-rl-course/unit1/introduction
This article is part of the Deep Reinforcement Learning Class. A free course from beginner to expert. Check the syllabus here.

⚠️ A new updated version of this article is available here 👉 https://huggingface.co/deep-rl-course/unit1/introduction
This article is part of the Deep Reinforcement Learning Class. A free course from beginner to expert. Check the syllabus here.
In the last unit, we learned our first reinforcement learning algorithm: Q-Learning, implemented it from scratch, and trained it in two environments, FrozenLake-v1 ☃️ and Taxi-v3 🚕.
We got excellent results with this simple algorithm. But these environments were relatively simple because the State Space was discrete and small (14 different states for FrozenLake-v1 and 500 for Taxi-v3).
But as we'll see, producing and updating a Q-table can become ineffective in large state space environments.
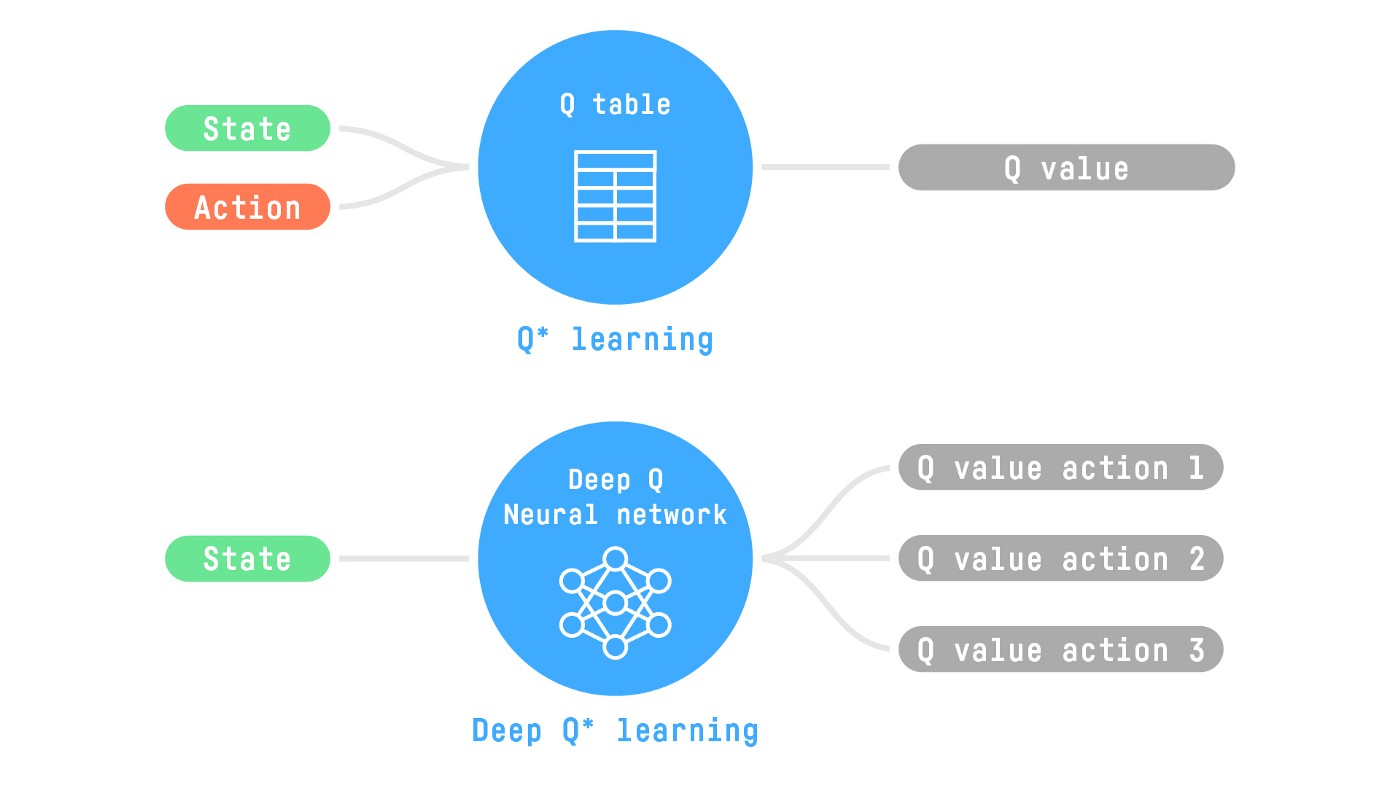
So today, we'll study our first Deep Reinforcement Learning agent: Deep Q-Learning. Instead of using a Q-table, Deep Q-Learning uses a Neural Network that takes a state and approximates Q-values for each action based on that state.
And we'll train it to play Space Invaders and other Atari environments using RL-Zoo, a training framework for RL using Stable-Baselines that provides scripts for training, evaluating agents, tuning hyperparameters, plotting results, and recording videos.

So let’s get started! 🚀
To be able to understand this unit, you need to understand Q-Learning first.
From Q-Learning to Deep Q-Learning
We learned that Q-Learning is an algorithm we use to train our Q-Function, an action-value function that determines the value of being at a particular state and taking a specific action at that state.
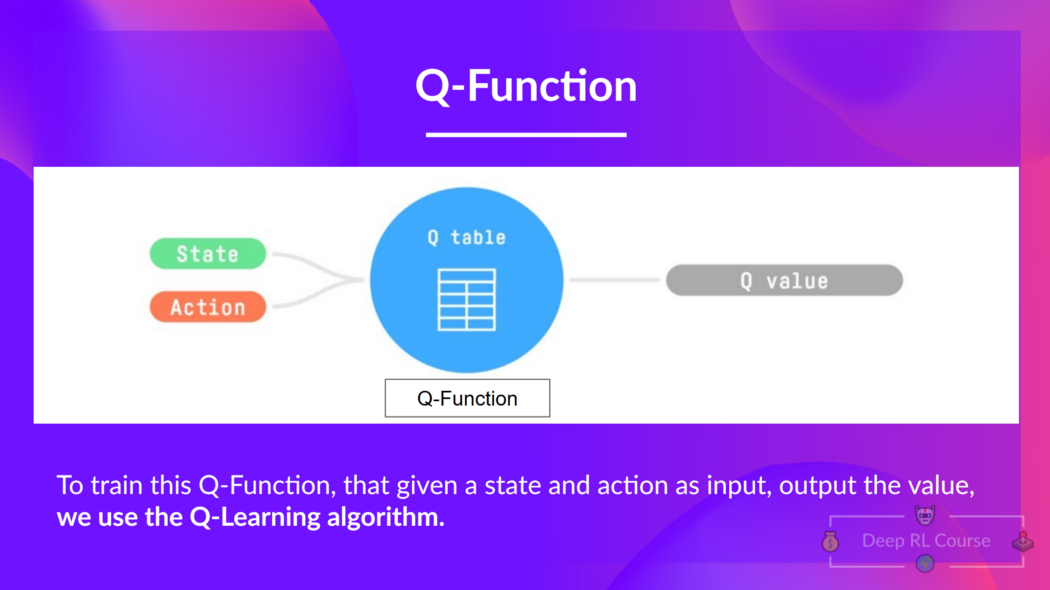
The Q comes from "the Quality" of that action at that state.
Internally, our Q-function has a Q-table, a table where each cell corresponds to a state-action pair value. Think of this Q-table as the memory or cheat sheet of our Q-function.
The problem is that Q-Learning is a tabular method. Aka, a problem in which the state and actions spaces are small enough to approximate value functions to be represented as arrays and tables. And this is not scalable.
Q-Learning was working well with small state space environments like:
- FrozenLake, we had 14 states.
- Taxi-v3, we had 500 states.
But think of what we're going to do today: we will train an agent to learn to play Space Invaders using the frames as input.
As Nikita Melkozerov mentioned, Atari environments have an observation space with a shape of (210, 160, 3), containing values ranging from 0 to 255 so that gives us 256^(210x160x3) = 256^100800 (for comparison, we have approximately 10^80 atoms in the observable universe).
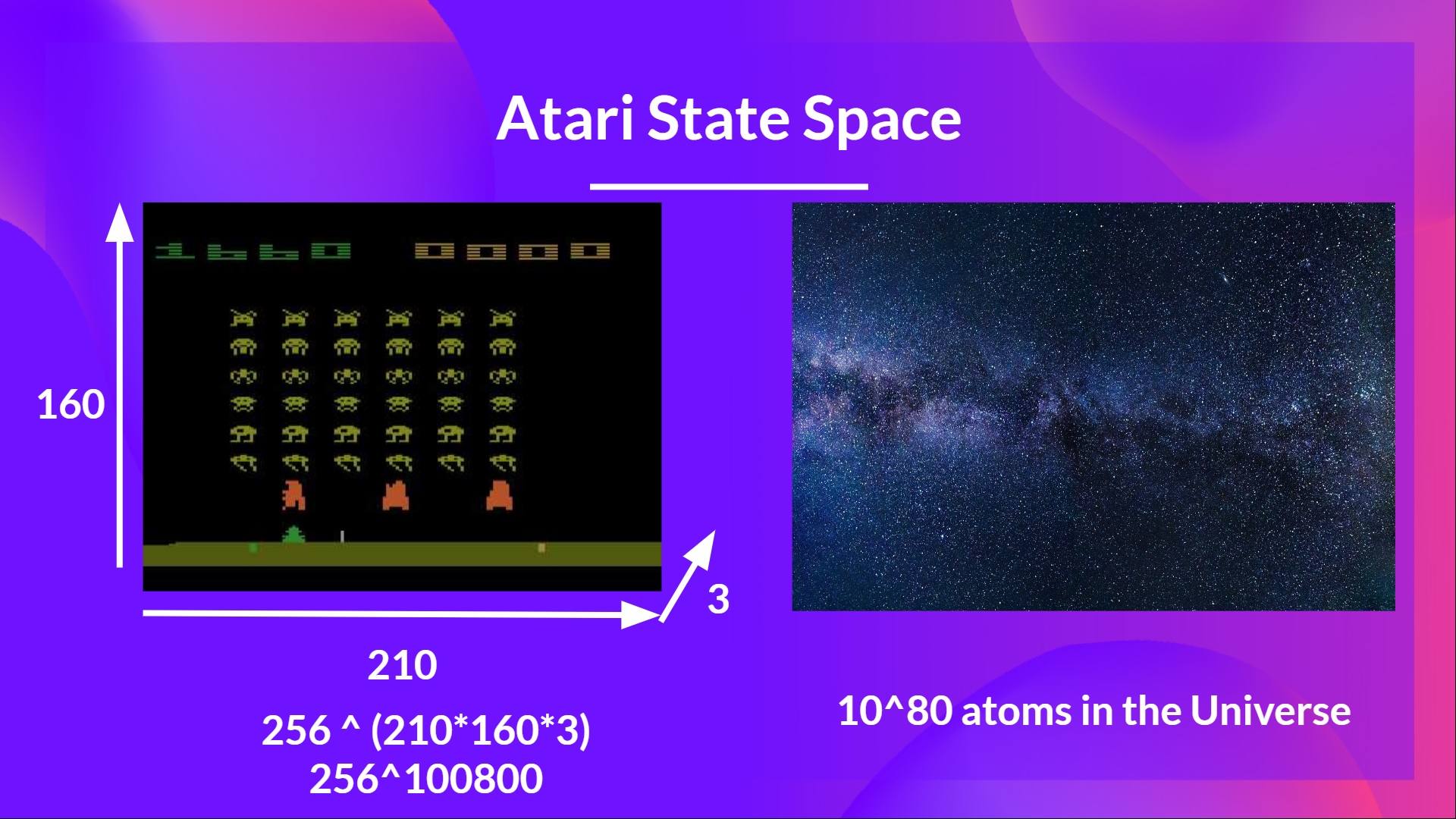
Therefore, the state space is gigantic; hence creating and updating a Q-table for that environment would not be efficient. In this case, the best idea is to approximate the Q-values instead of a Q-table using a parametrized Q-function .
This neural network will approximate, given a state, the different Q-values for each possible action at that state. And that's exactly what Deep Q-Learning does.
Now that we understand Deep Q-Learning, let's dive deeper into the Deep Q-Network.
The Deep Q-Network (DQN)
This is the architecture of our Deep Q-Learning network:
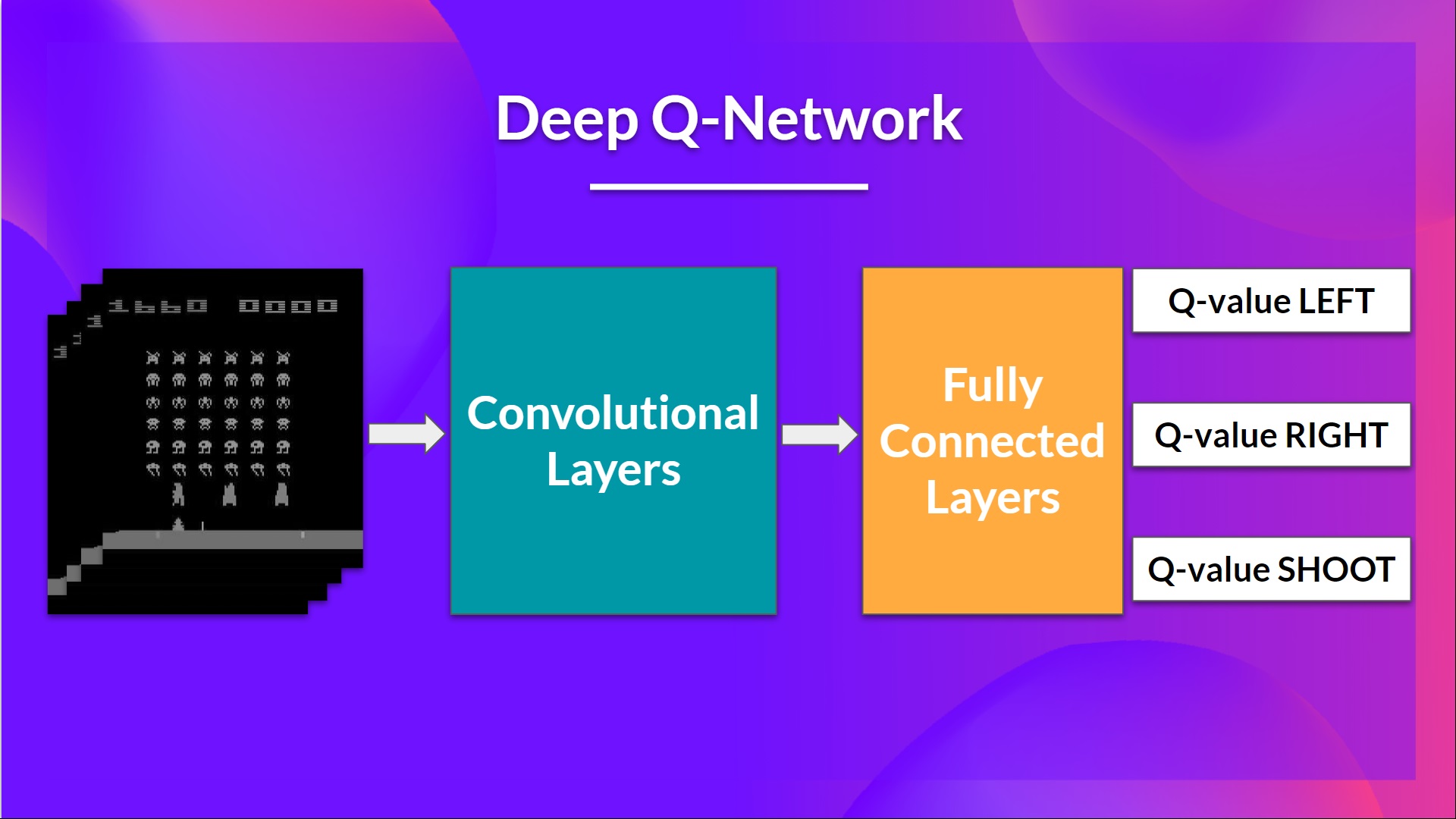
As input, we take a stack of 4 frames passed through the network as a state and output a vector of Q-values for each possible action at that state. Then, like with Q-Learning, we just need to use our epsilon-greedy policy to select which action to take.
When the Neural Network is initialized, the Q-value estimation is terrible. But during training, our Deep Q-Network agent will associate a situation with appropriate action and learn to play the game well.
Preprocessing the input and temporal limitation
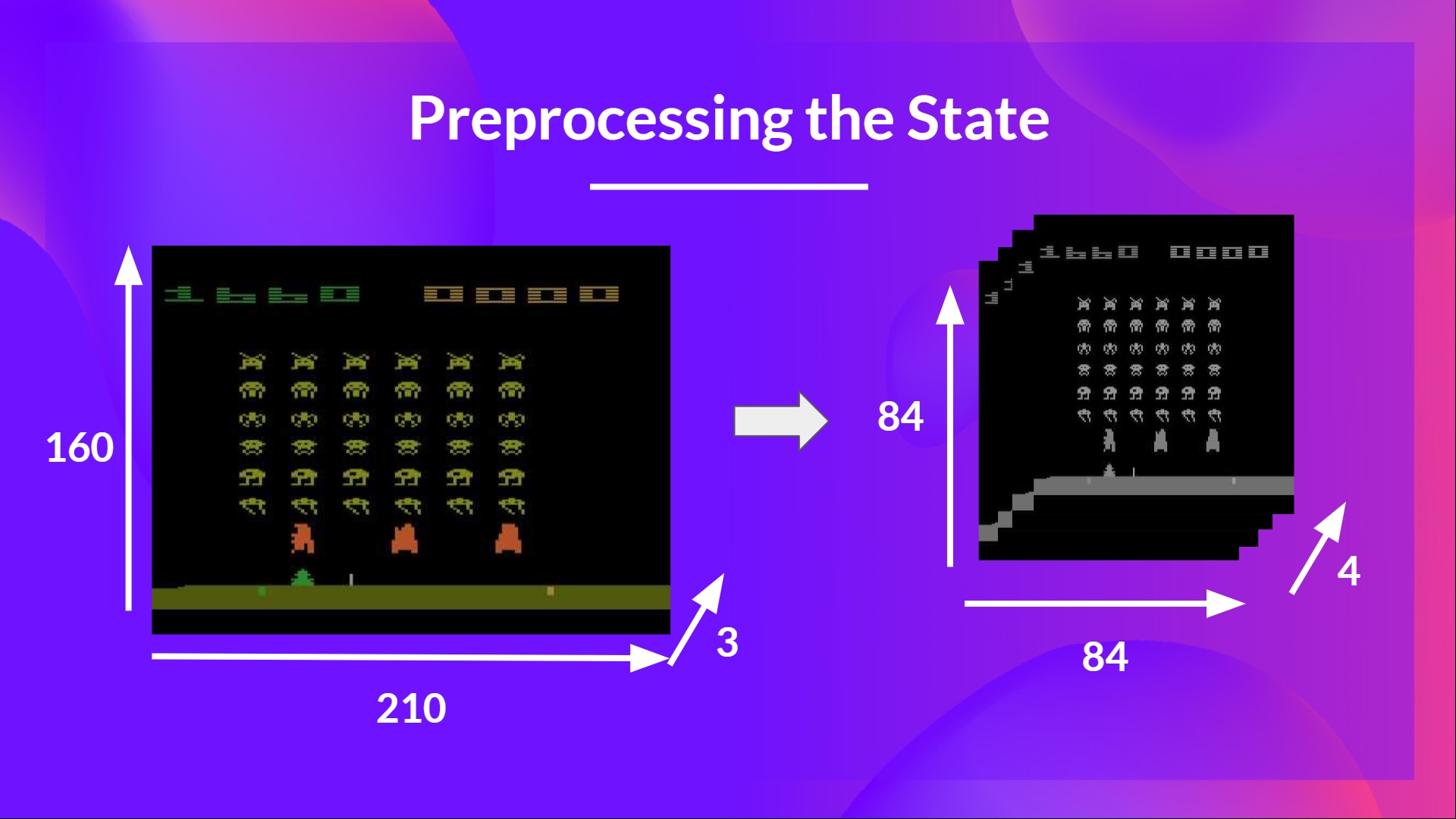
We mentioned that we preprocess the input. It’s an essential step since we want to reduce the complexity of our state to reduce the computation time needed for training.
So what we do is reduce the state space to 84x84 and grayscale it (since the colors in Atari environments don't add important information). This is an essential saving since we reduce our three color channels (RGB) to 1.
We can also crop a part of the screen in some games if it does not contain important information. Then we stack four frames together.
Why do we stack four frames together? We stack frames together because it helps us handle the problem of temporal limitation. Let’s take an example with the game of Pong. When you see this frame:

Can you tell me where the ball is going? No, because one frame is not enough to have a sense of motion! But what if I add three more frames? Here you can see that the ball is going to the right.
 That’s why, to capture temporal information, we stack four frames together.
That’s why, to capture temporal information, we stack four frames together.
Then, the stacked frames are processed by three convolutional layers. These layers allow us to capture and exploit spatial relationships in images. But also, because frames are stacked together, you can exploit some spatial properties across those frames.
Finally, we have a couple of fully connected layers that output a Q-value for each possible action at that state.

So, we see that Deep Q-Learning is using a neural network to approximate, given a state, the different Q-values for each possible action at that state. Let’s now study the Deep Q-Learning algorithm.
The Deep Q-Learning Algorithm
We learned that Deep Q-Learning uses a deep neural network to approximate the different Q-values for each possible action at a state (value-function estimation).
The difference is that, during the training phase, instead of updating the Q-value of a state-action pair directly as we have done with Q-Learning:

In Deep Q-Learning, we create a Loss function between our Q-value prediction and the Q-target and use Gradient Descent to update the weights of our Deep Q-Network to approximate our Q-values better.

The Deep Q-Learning training algorithm has two phases:
- Sampling: we perform actions and store the observed experiences tuples in a replay memory.
- Training: Select the small batch of tuple randomly and learn from it using a gradient descent update step.

But, this is not the only change compared with Q-Learning. Deep Q-Learning training might suffer from instability, mainly because of combining a non-linear Q-value function (Neural Network) and bootstrapping (when we update targets with existing estimates and not an actual complete return).
To help us stabilize the training, we implement three different solutions:
- Experience Replay, to make more efficient use of experiences.
- Fixed Q-Target to stabilize the training.
- Double Deep Q-Learning, to handle the problem of the overestimation of Q-values.
Experience Replay to make more efficient use of experiences
Why do we create a replay memory?
Experience Replay in Deep Q-Learning has two functions:
- Make more efficient use of the experiences during the training.
- Experience replay helps us make more efficient use of the experiences during the training. Usually, in online reinforcement learning, we interact in the environment, get experiences (state, action, reward, and next state), learn from them (update the neural network) and discard them.
- But with experience replay, we create a replay buffer that saves experience samples that we can reuse during the training.

⇒ This allows us to learn from individual experiences multiple times.
- Avoid forgetting previous experiences and reduce the correlation between experiences.
- The problem we get if we give sequential samples of experiences to our neural network is that it tends to forget the previous experiences as it overwrites new experiences. For instance, if we are in the first level and then the second, which is different, our agent can forget how to behave and play in the first level.
The solution is to create a Replay Buffer that stores experience tuples while interacting with the environment and then sample a small batch of tuples. This prevents the network from only learning about what it has immediately done.
Experience replay also has other benefits. By randomly sampling the experiences, we remove correlation in the observation sequences and avoid action values from oscillating or diverging catastrophically.
In the Deep Q-Learning pseudocode, we see that we initialize a replay memory buffer D from capacity N (N is an hyperparameter that you can define). We then store experiences in the memory and sample a minibatch of experiences to feed the Deep Q-Network during the training phase.

Fixed Q-Target to stabilize the training
When we want to calculate the TD error (aka the loss), we calculate the difference between the TD target (Q-Target) and the current Q-value (estimation of Q).
But we don’t have any idea of the real TD target. We need to estimate it. Using the Bellman equation, we saw that the TD target is just the reward of taking that action at that state plus the discounted highest Q value for the next state.

However, the problem is that we are using the same parameters (weights) for estimating the TD target and the Q value. Consequently, there is a significant correlation between the TD target and the parameters we are changing.
Therefore, it means that at every step of training, our Q values shift but also the target value shifts. So, we’re getting closer to our target, but the target is also moving. It’s like chasing a moving target! This led to a significant oscillation in training.
It’s like if you were a cowboy (the Q estimation) and you want to catch the cow (the Q-target), you must get closer (reduce the error).
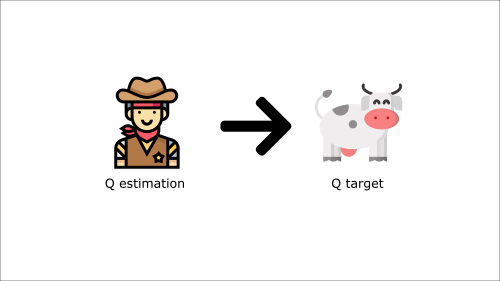
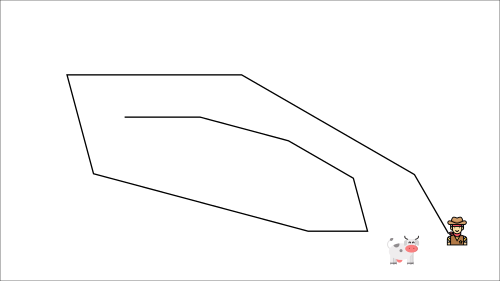
At each time step, you’re trying to approach the cow, which also moves at each time step (because you use the same parameters).

 This leads to a bizarre path of chasing (a significant oscillation in training).
This leads to a bizarre path of chasing (a significant oscillation in training).
Instead, what we see in the pseudo-code is that we:
- Use a separate network with a fixed parameter for estimating the TD Target
- Copy the parameters from our Deep Q-Network at every C step to update the target network.

Double DQN
Double DQNs, or Double Learning, were introduced by Hado van Hasselt. This method handles the problem of the overestimation of Q-values.
To understand this problem, remember how we calculate the TD Target:
We face a simple problem by calculating the TD target: how are we sure that the best action for the next state is the action with the highest Q-value?
We know that the accuracy of Q values depends on what action we tried and what neighboring states we explored.
Consequently, we don’t have enough information about the best action to take at the beginning of the training. Therefore, taking the maximum Q value (which is noisy) as the best action to take can lead to false positives. If non-optimal actions are regularly given a higher Q value than the optimal best action, the learning will be complicated.
The solution is: when we compute the Q target, we use two networks to decouple the action selection from the target Q value generation. We:
- Use our DQN network to select the best action to take for the next state (the action with the highest Q value).
- Use our Target network to calculate the target Q value of taking that action at the next state.
Therefore, Double DQN helps us reduce the overestimation of q values and, as a consequence, helps us train faster and have more stable learning.
Since these three improvements in Deep Q-Learning, many have been added such as Prioritized Experience Replay, Dueling Deep Q-Learning. They’re out of the scope of this course but if you’re interested, check the links we put in the reading list. 👉 https://github.com/huggingface/deep-rl-class/blob/main/unit3/README.md
Now that you've studied the theory behind Deep Q-Learning, you’re ready to train your Deep Q-Learning agent to play Atari Games. We'll start with Space Invaders, but you'll be able to use any Atari game you want 🔥
We're using the RL-Baselines-3 Zoo integration, a vanilla version of Deep Q-Learning with no extensions such as Double-DQN, Dueling-DQN, and Prioritized Experience Replay.
Start the tutorial here 👉 https://colab.research.google.com/github/huggingface/deep-rl-class/blob/main/unit3/unit3.ipynb
The leaderboard to compare your results with your classmates 🏆 👉 https://huggingface.co/spaces/chrisjay/Deep-Reinforcement-Learning-Leaderboard

Congrats on finishing this chapter! There was a lot of information. And congrats on finishing the tutorial. You’ve just trained your first Deep Q-Learning agent and shared it on the Hub 🥳.
That’s normal if you still feel confused with all these elements. This was the same for me and for all people who studied RL.
Take time to really grasp the material before continuing.
Don't hesitate to train your agent in other environments (Pong, Seaquest, QBert, Ms Pac Man). The best way to learn is to try things on your own!
We published additional readings in the syllabus if you want to go deeper 👉 https://github.com/huggingface/deep-rl-class/blob/main/unit3/README.md
In the next unit, we’re going to learn about Policy Gradients methods.
And don't forget to share with your friends who want to learn 🤗 !
Finally, we want to improve and update the course iteratively with your feedback. If you have some, please fill this form 👉 https://forms.gle/3HgA7bEHwAmmLfwh9

