DART-Math: Difficulty-Aware Rejection Tuning for Mathematical Problem-Solving

📝 Paper@arXiv | 🤗 Datasets&Models@HF | 🐱 Code@GitHub

🐦 Thread@X(Twitter) | 🐶 中文博客@知乎 | 📊 Leaderboard@PapersWithCode | 📑 BibTeX

🔥 News!!!
Excited to find our DART-Math-DSMath-7B (Prop2Diff) comparable to the AIMO winner NuminaMath-7B on CoT,
but based solely on MATH & GSM8K prompt set, leaving much room to improve!
Besides, our DART method is also fully compatible with tool-integrated reasoning.
Join the discussion in this page or under this X thread!

✨ TL;DR

Previous synthetic datasets for mathematical instruction-tuning are generally biased towards easy queries. Difficulty-Aware Rejecting Tuning (DART) eliminates this bias by allocating more data synthesis budget to difficult queries, achieving performance superior to or comparable with SotA.

🎁 Takeaways

1. Current SotA mathematical instruction tuning datasets (e.g., MetaMath) mostly exhibit a bias towards simple queries, and usually have no response samples for the most challenging queries.
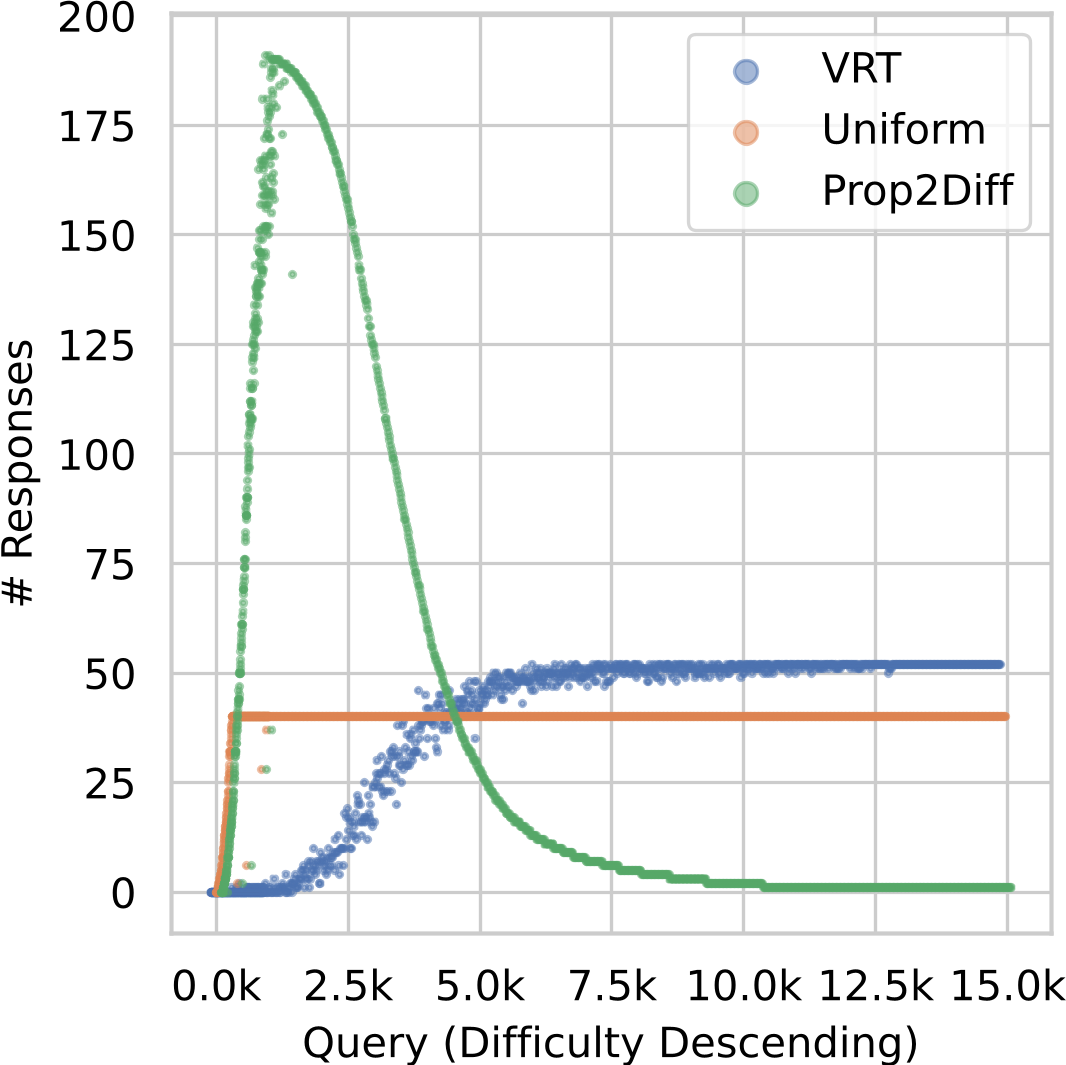
2. The bias towards simple queries primarily stems from the Vanilla Rejection Sampling method employed, which samples an equal number of raw responses for each query and filters to retain only correct responses. However, the probability of sampling correct responses for difficult queries is significantly lower, sometimes zero.
3. Small open-source models are capable of synthesizing correct responses for the vast majority of queries. For instance, the DeepSeekMath-7B series models can correctly answer at least once within 100 attempts for >90% of queries on MATH500, and at least once within 1000 attempts for >99% of queries.
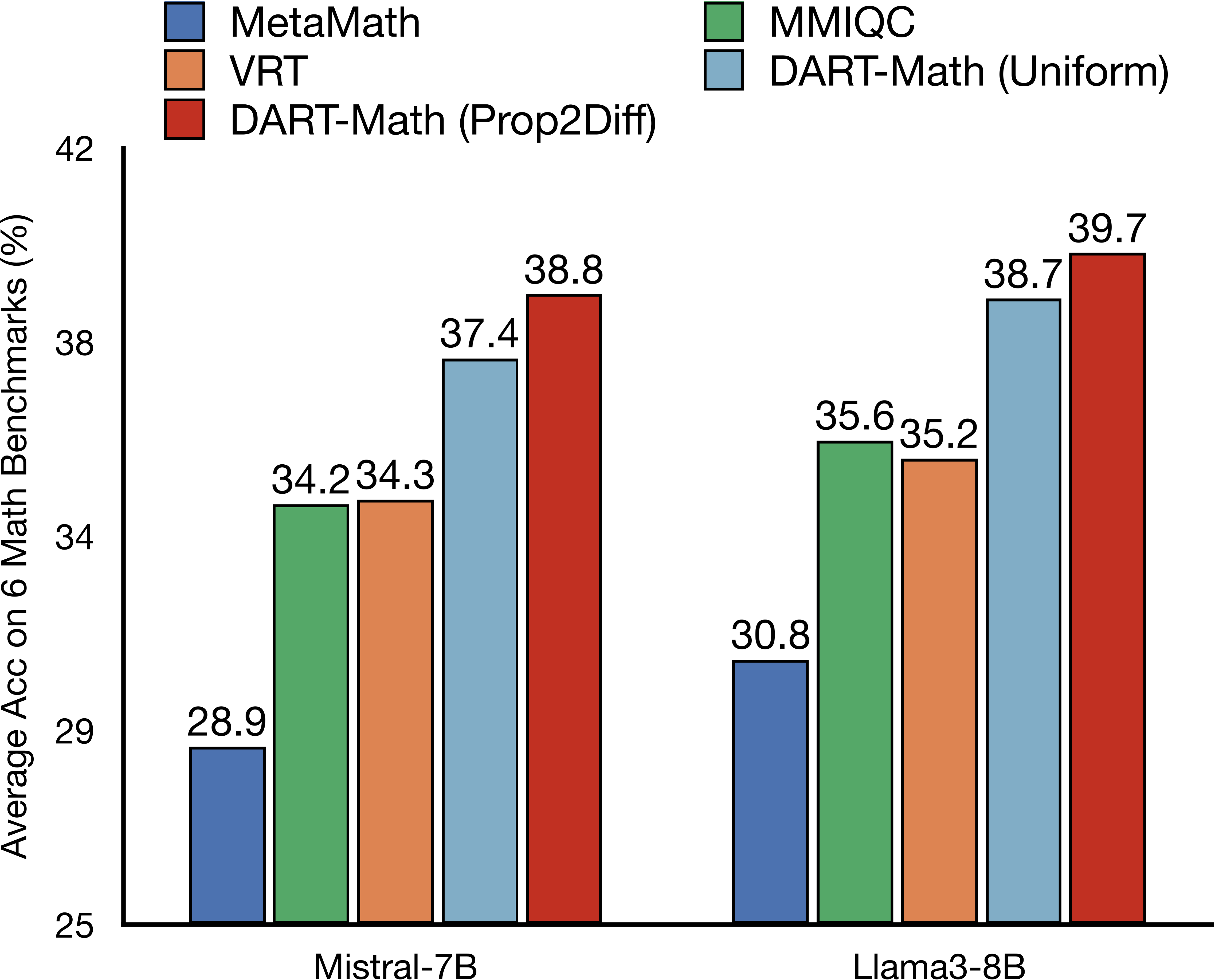
4. Difficulty-Aware Rejection Tuning (DART) synthesizes datasets that place greater emphasis on difficult queries by conducting more sampling for challenging queries. Compared to Vanilla Rejection Tuning (VRT), DART consistently achieves significant improvements across 4 pre-trained models and 6 mathematical problem-solving evaluation benchmarks.
5. The DART-Math dataset, synthesized without relying on proprietary models such as GPT-4, is currently the most effective and cost-efficient publicly available instruction tuning dataset for mathematical problem-solving tasks. Models trained on this dataset, referred to as DART-Math models, have achieved SotA performance on multiple in-domain and out-of-domain mathematical problem-solving evaluation benchmarks.

📝 论文@arXiv | 🤗 数据&模型@HF | 🐱 代码@GitHub

🐦 Thread@X(Twitter) | 🐶 中文博客@知乎 | 📊 排行榜@PapersWithCode | 📑 BibTeX

🔥 号外！ 我们的 DART-Math-DSMath-7B (Prop2Diff) 的性能接近了 AIMO 冠军 NuminaMath-7B ，仅基于规模有限的 MATH 和 GSM8K 的 prompt 数据集！此外，我们的 DART 方法 也完全 适配工具集成推理（Tool-Integrated Reasoning）。在本页面中或该 X thread 下与我们一起讨论吧！

✨ 太长不看版

现有的用于数学推理指令微调的合成数据集普遍偏向于简单查询，难度感知拒绝调优（Difficulty-Aware Rejecting Tuning，DART）通过为困难查询分配更多数据合成资源，消除了这一偏向，并在多个数学推理测试基准上取得/接近了 SotA。

🎁 划重点

1. 现有最先进的数学指令微调数据集（例如 MetaMath）普遍偏向于简单查询，且对于最困难的查询经常出现没有任何响应样本的情况。
2. 对于简单查询的偏向主要来源于它们使用的原始拒绝采样（Vanilla Rejection Sampling） 方法，其对每个查询采样相同数量的原始响应，并过滤以仅保留正确响应，但为困难查询采样正确响应的概率显著更低，有时接近于 0。
3. 小规模的开源模型就能对绝大部分查询合成正确响应。 例如，DeepSeekMath-7B 系列模型，在 MATH500 上，对于 >90% 的查询，都能在 100 次尝试内至少正确回答一次；对于>99% 的查询，都能在 1000 次尝试内至少正确回答一次。
4. 难度感知拒绝调优 （Difficulty-Aware Rejecting Tuning，DART） 通过对困难查询进行更多的采样，合成更重视困难查询的数据集，与 原始拒绝调优（Vanalla Rejection Tuning, VRT） 相比，在 4 个预训练模型上与 6 个数学问题求解评测基准上一致取得了显著提升。
5. 不依赖于 GPT-4 等专有模型合成的 DART-Math 数据集是目前数学问题求解任务上最有效且最具性价比的公开指令调优数据集，在其上训练的 DART-Math 模型在多个领域内与领域外数学问题求解评测基准上实现了 SotA。