Spaces:
Running
Running
Commit
·
1858a22
1
Parent(s):
4c67c21
Add example plot to examples of docs
Browse files- docs/examples.md +109 -0
- docs/images/example_plot.png +0 -0
docs/examples.md
ADDED
|
@@ -0,0 +1,109 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
# Examples
|
| 2 |
+
|
| 3 |
+
### Preamble
|
| 4 |
+
|
| 5 |
+
```python
|
| 6 |
+
import numpy as np
|
| 7 |
+
from pysr import *
|
| 8 |
+
```
|
| 9 |
+
|
| 10 |
+
We'll also set up some default options that will
|
| 11 |
+
make these simple searches go faster (but are less optimal
|
| 12 |
+
for more complex searches).
|
| 13 |
+
|
| 14 |
+
```python
|
| 15 |
+
kwargs = dict(populations=5, niterations=5, annealing=True)
|
| 16 |
+
```
|
| 17 |
+
|
| 18 |
+
1. Simple search
|
| 19 |
+
|
| 20 |
+
Here's a simple example where we turn off multiprocessing,
|
| 21 |
+
and find the expression `2 cos(x3) + x0^2 - 2`.
|
| 22 |
+
|
| 23 |
+
```python
|
| 24 |
+
X = 2 * np.random.randn(100, 5)
|
| 25 |
+
y = 2 * np.cos(X[:, 3]) + X[:, 0] ** 2 - 2
|
| 26 |
+
expressions = pysr(X, y, binary_operators=["+", "-", "*", "/"], **kwargs)
|
| 27 |
+
print(best(expressions))
|
| 28 |
+
```
|
| 29 |
+
|
| 30 |
+
2. Custom operator
|
| 31 |
+
|
| 32 |
+
Here, we define a custom operator and use it to find an expression:
|
| 33 |
+
|
| 34 |
+
```python
|
| 35 |
+
X = 2 * np.random.randn(100, 5)
|
| 36 |
+
y = 1 / X[:, 0]
|
| 37 |
+
expressions = pysr(
|
| 38 |
+
X,
|
| 39 |
+
y,
|
| 40 |
+
binary_operators=["plus", "mult"],
|
| 41 |
+
unary_operators=["inv(x) = 1/x"],
|
| 42 |
+
**kwargs
|
| 43 |
+
)
|
| 44 |
+
print(best(expressions))
|
| 45 |
+
```
|
| 46 |
+
|
| 47 |
+
3. Multiple outputs
|
| 48 |
+
|
| 49 |
+
Here, we do the same thing, but with multiple expressions at once,
|
| 50 |
+
each requiring a different feature.
|
| 51 |
+
```python
|
| 52 |
+
X = 2 * np.random.randn(100, 5)
|
| 53 |
+
y = 1 / X[:, [0, 1, 2]]
|
| 54 |
+
expressions = pysr(
|
| 55 |
+
X,
|
| 56 |
+
y,
|
| 57 |
+
binary_operators=["plus", "mult"],
|
| 58 |
+
unary_operators=["inv(x) = 1/x"],
|
| 59 |
+
**kwargs
|
| 60 |
+
)
|
| 61 |
+
```
|
| 62 |
+
|
| 63 |
+
4. Plotting an expression
|
| 64 |
+
|
| 65 |
+
Here, let's use the same equations, but get a format we can actually
|
| 66 |
+
use and test. We can add this option after a search via the `get_hof`
|
| 67 |
+
function:
|
| 68 |
+
|
| 69 |
+
```python
|
| 70 |
+
expressions = get_hof(extra_sympy_mappings={"inv": lambda x: 1/x})
|
| 71 |
+
```
|
| 72 |
+
If you look at the lists of expressions before and after, you will
|
| 73 |
+
see that the sympy format now has replaced `inv` with `1/`.
|
| 74 |
+
|
| 75 |
+
For now, let's consider the expressions for output 0:
|
| 76 |
+
```python
|
| 77 |
+
expressions = expressions[0]
|
| 78 |
+
```
|
| 79 |
+
This is a pandas table, which we can filter:
|
| 80 |
+
```python
|
| 81 |
+
best_expression = expressions.iloc[expressions.MSE.argmin()]
|
| 82 |
+
```
|
| 83 |
+
We can see the LaTeX version of this with:
|
| 84 |
+
```python
|
| 85 |
+
import sympy
|
| 86 |
+
sympy.latex(best_expression.sympy_format)
|
| 87 |
+
```
|
| 88 |
+
|
| 89 |
+
We can access the numpy version with:
|
| 90 |
+
```python
|
| 91 |
+
f = best_expression.lambda_format
|
| 92 |
+
print(f)
|
| 93 |
+
```
|
| 94 |
+
|
| 95 |
+
Which shows a PySR object on numpy code:
|
| 96 |
+
```
|
| 97 |
+
>> PySRFunction(X=>1/x0)
|
| 98 |
+
```
|
| 99 |
+
|
| 100 |
+
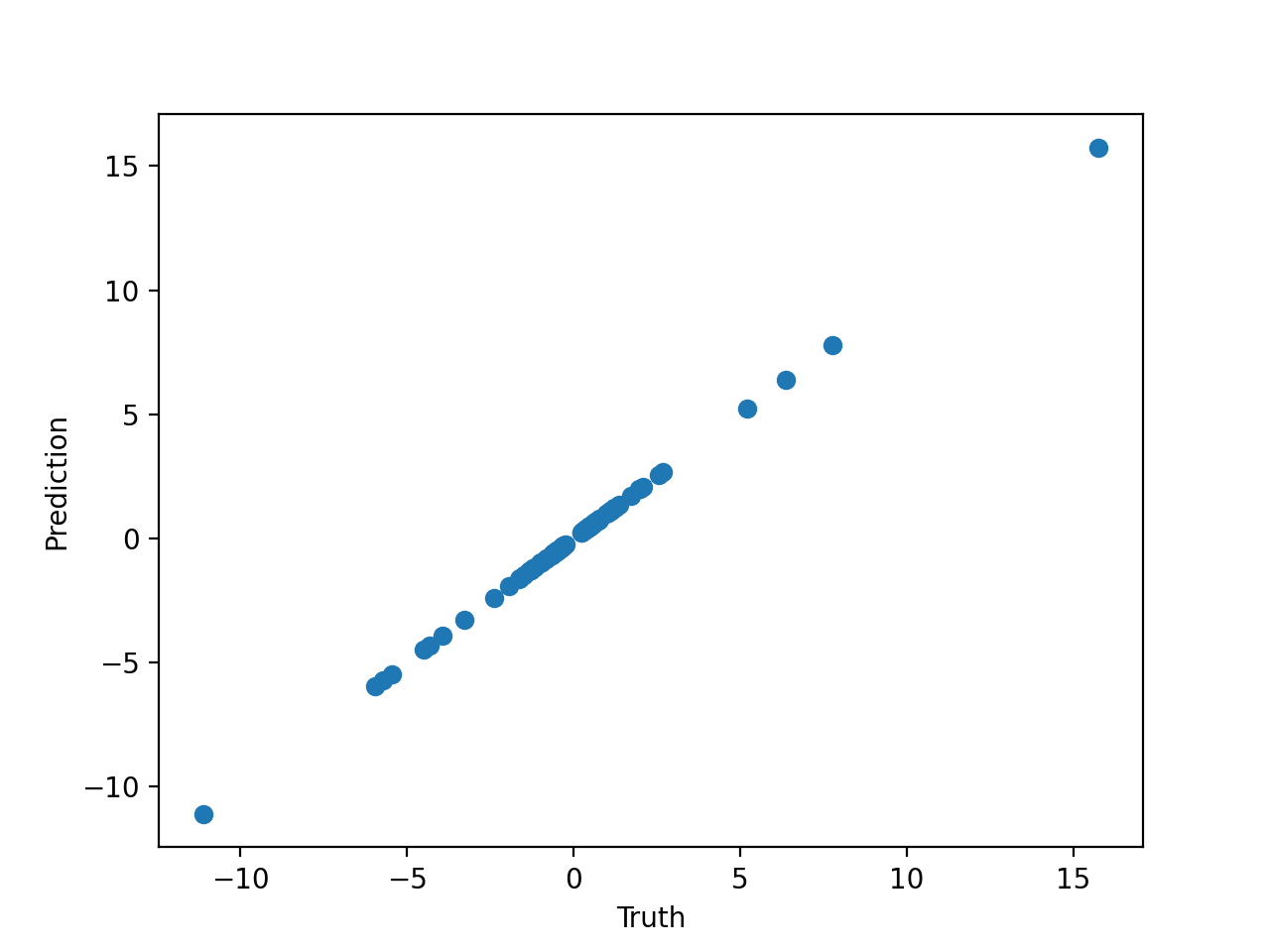
Let's plot this against the truth:
|
| 101 |
+
```python
|
| 102 |
+
from matplotlib import pyplot as plt
|
| 103 |
+
plt.scatter(y[:, 0], f(X))
|
| 104 |
+
plt.xlabel('Truth')
|
| 105 |
+
plt.ylabel('Prediction')
|
| 106 |
+
plt.show()
|
| 107 |
+
```
|
| 108 |
+
Which gives us:
|
| 109 |
+

|
docs/images/example_plot.png
ADDED
|