Adding two entries to papers.yml (#192)

* Added two entries to papers.yml

* Add files for papers.yml

* Remove unused image

* Fix formatting issues in paper submission

* Fix mathjax errors

Co-authored-by: MilesCranmer <miles.cranmer@gmail.com>

docs/papers.yml

@@ -131,4 +131,54 @@ papers:
     abstract: "The conjoining of dynamical systems and deep learning has become a topic of great interest. In particular, neural differential equations (NDEs) demonstrate that neural networks and differential equation are two sides of the same coin. Traditional parameterised differential equations are a special case. Many popular neural network architectures, such as residual networks and recurrent networks, are discretisations. NDEs are suitable for tackling generative problems, dynamical systems, and time series (particularly in physics, finance, ...) and are thus of interest to both modern machine learning and traditional mathematical modelling. NDEs offer high-capacity function approximation, strong priors on model space, the ability to handle irregular data, memory efficiency, and a wealth of available theory on both sides. This doctoral thesis provides an in-depth survey of the field. Topics include: neural ordinary differential equations (e.g. for hybrid neural/mechanistic modelling of physical systems); neural controlled differential equations (e.g. for learning functions of irregular time series); and neural stochastic differential equations (e.g. to produce generative models capable of representing complex stochastic dynamics, or sampling from complex high-dimensional distributions). Further topics include: numerical methods for NDEs (e.g. reversible differential equations solvers, backpropagation through differential equations, Brownian reconstruction); symbolic regression for dynamical systems (e.g. via regularised evolution); and deep implicit models (e.g. deep equilibrium models, differentiable optimisation). We anticipate this thesis will be of interest to anyone interested in the marriage of deep learning with dynamical systems, and hope it will provide a useful reference for the current state of the art."
     link: https://arxiv.org/abs/2202.02435
     date: 2022-02-04
-    image: kidger_thesis.png
+    image: kidger_thesis.png
+  - title: "Augmenting astrophysical scaling relations with machine learning: application to reducing the SZ flux-mass scatter"
+    authors:
+      - Digvijay Wadekar (1)
+      - Leander Thiele (2)
+      - Francisco Villaescusa-Navarro (3)
+      - J. Colin Hill (4)
+      - Miles Cranmer (2)
+      - David N. Spergel (3)
+      - Nicholas Battaglia (5)
+      - Daniel Anglés-Alcázar (6)
+      - Lars Hernquist (7)
+      - Shirley Ho (3)
+    affiliations:
+      1: Institute for Advanced Study
+      2: Princeton University
+      3: Flatiron Institute
+      4: Columbia University
+      5: Cornell University
+      6: University of Connecticut
+      7: Havard University
+    link: https://arxiv.org/abs/2201.01305
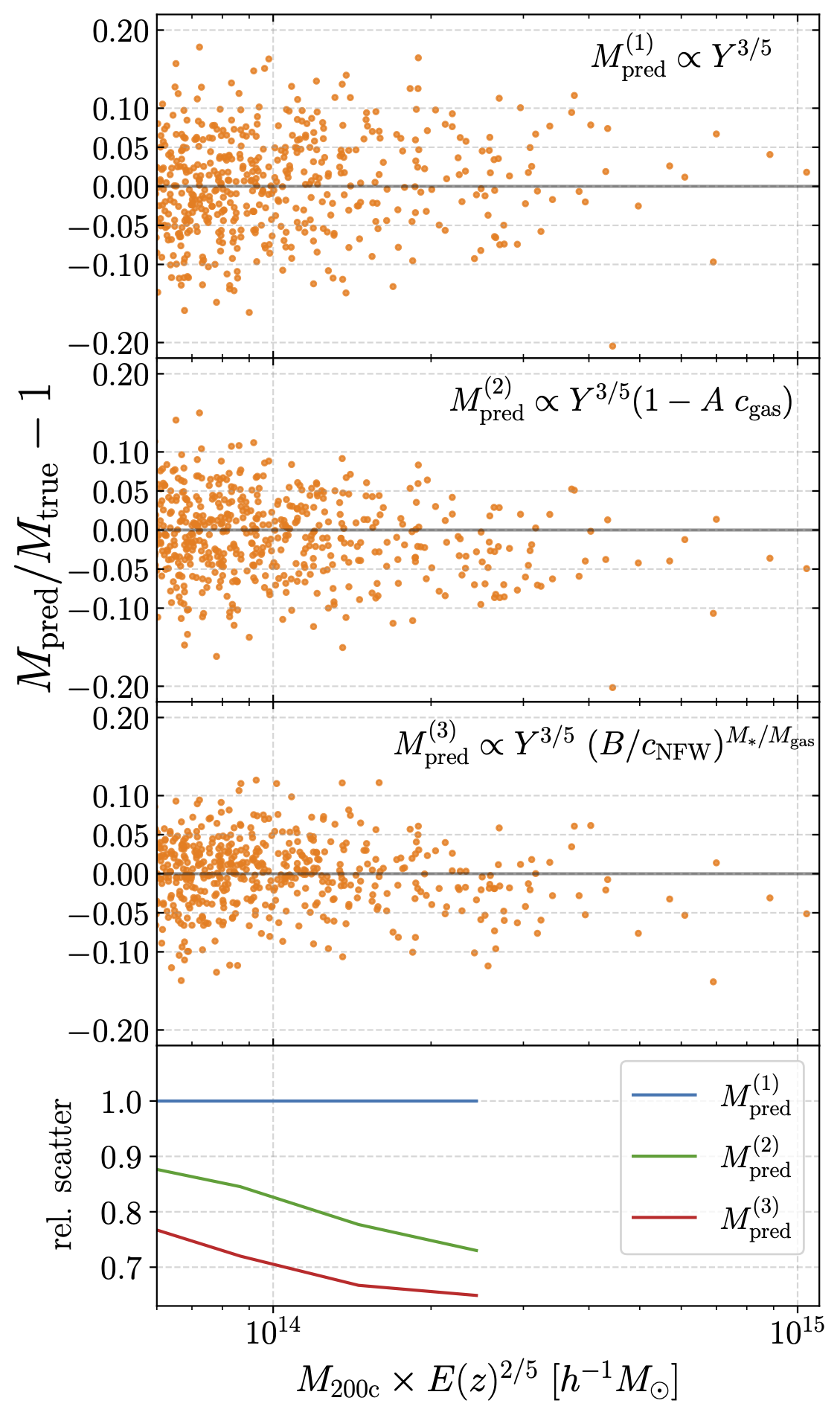
+    abstract: "Complex systems (stars, supernovae, galaxies, and clusters) often exhibit low scatter relations between observable properties (e.g., luminosity, velocity dispersion, oscillation period, temperature). These scaling relations can illuminate the underlying physics and can provide observational tools for estimating masses and distances. Machine learning can provide a fast and systematic way to search for new scaling relations (or for simple extensions to existing relations) in abstract high-dimensional parameter spaces. We use a machine learning tool called symbolic regression (SR), which models the patterns in a given dataset in the form of analytic equations. We focus on the Sunyaev-Zeldovich flux-cluster mass relation (Y-M), the scatter in which affects inference of cosmological parameters from cluster abundance data. Using SR on the data from the IllustrisTNG hydrodynamical simulation, we find a new proxy for cluster mass which combines $Y_{SZ}$ and concentration of ionized gas (cgas): $M \\propto Y_{\\text{conc}}^{3/5} \\equiv Y_{SZ}^{3/5} (1 - A c_\\text{gas})$. Yconc reduces the scatter in the predicted M by ~ 20 - 30% for large clusters (M > 10^14 M⊙/h) at both high and low redshifts, as compared to using just $Y_{SZ}$. We show that the dependence on cgas is linked to cores of clusters exhibiting larger scatter than their outskirts. Finally, we test Yconc on clusters from simulations of the CAMELS project and show that Yconc is robust against variations in cosmology, astrophysics, subgrid physics, and cosmic variance. Our results and methodology can be useful for accurate multiwavelength cluster mass estimation from current and upcoming CMB and X-ray surveys like ACT, SO, SPT, eROSITA and CMB-S4."
+    image: SyReg_GasConc.png
+    date: 2022-01-05
+  - title: "The SZ flux-mass (Y-M) relation at low halo masses: improvements with symbolic regression and strong constraints on baryonic feedback"
+    authors:
+      - Digvijay Wadekar (1)
+      - Leander Thiele (2)
+      - J. Colin Hill (3)
+      - Shivam Pandey (4)
+      - Francisco Villaescusa-Navarro (5)
+      - David N. Spergel (5)
+      - Miles Cranmer (2)
+      - Daisuke Nagai (6)
+      - Daniel Anglés-Alcázar (7)
+      - Shirley Ho (5)
+      - Lars Hernquist (8)
+    affiliations:
+      1: Institute for Advanced Study
+      2: Princeton University
+      3: Columbia University
+      4: University of Pennsylvania
+      5: Flatiron Institute
+      6: Yale University
+      7: University of Connecticut
+      8: Havard University
+    link: https://arxiv.org/abs/2209.02075
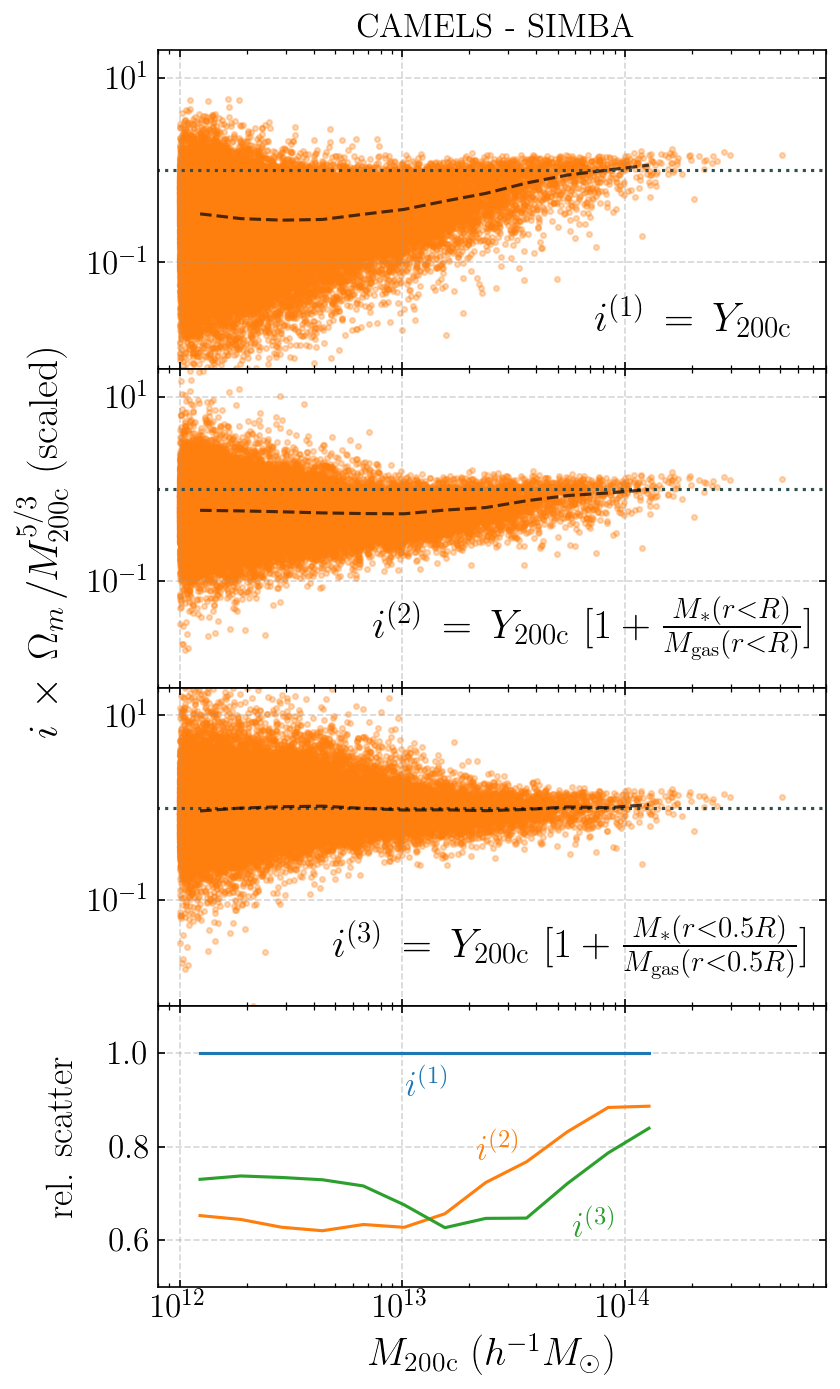
+    abstract: "Ionized gas in the halo circumgalactic medium leaves an imprint on the cosmic microwave background via the thermal Sunyaev-Zeldovich (tSZ) effect. Feedback from active galactic nuclei (AGN) and supernovae can affect the measurements of the integrated tSZ flux of halos ($Y_{SZ}$) and cause its relation with the halo mass ($Y_{SZ}-M$) to deviate from the self-similar power-law prediction of the virial theorem. We perform a comprehensive study of such deviations using CAMELS, a suite of hydrodynamic simulations with extensive variations in feedback prescriptions. We use a combination of two machine learning tools (random forest and symbolic regression) to search for analogues of the $Y-M$ relation which are more robust to feedback processes for low masses ($M \\leq 10^{14} M_{\\odot}/h$); we find that simply replacing $Y \\rightarrow Y(1+M_\\ast/M_{\\text{gas}})$ in the relation makes it remarkably self-similar. This could serve as a robust multiwavelength mass proxy for low-mass clusters and galaxy groups. Our methodology can also be generally useful to improve the domain of validity of other astrophysical scaling relations. We also forecast that measurements of the Y-M relation could provide percent-level constraints on certain combinations of feedback parameters and/or rule out a major part of the parameter space of supernova and AGN feedback models used in current state-of-the-art hydrodynamic simulations. Our results can be useful for using upcoming SZ surveys (e.g. SO, CMB-S4) and galaxy surveys (e.g. DESI and Rubin) to constrain the nature of baryonic feedback. Finally, we find that the an alternative relation, $Y-M_{\\ast}$, provides complementary information on feedback than $Y-M$."
+    image: Y_Mgal_Simba.png
+    date: 2022-09-05