Spaces:
Running
on
Zero
Running
on
Zero
First commit from github repo
Browse files- .gitattributes +1 -0
- README.md +124 -14
- app.py +470 -0
- assets/a4957-expertc.png +0 -0
- assets/a4957-input.png +0 -0
- assets/a4982-input.png +0 -0
- assets/a4984-input.png +0 -0
- assets/a4985-input.png +0 -0
- assets/a4986-input.png +0 -0
- assets/a4988-input.png +0 -0
- assets/a4990-input.png +0 -0
- assets/a4993-input.png +0 -0
- assets/a4994-input.png +0 -0
- assets/a4996-input.png +0 -0
- assets/a4998-input.png +0 -0
- assets/a5000-input.png +0 -0
- assets/architecture-overview.png +0 -0
- assets/thumbnail.png +0 -0
- configs/mit5k_dpe_config.yaml +96 -0
- configs/mit5k_upe_config.yaml +90 -0
- data/datasets.py +109 -0
- data/image_transformations.py +61 -0
- mit5k_ids_filepath/dpe/images_test.txt +50 -0
- mit5k_ids_filepath/dpe/images_train.txt +62 -0
- mit5k_ids_filepath/dpe/images_valid.txt +2250 -0
- mit5k_ids_filepath/upe_uegan/images_test.txt +500 -0
- mit5k_ids_filepath/upe_uegan/images_train.txt +4500 -0
- models/attention_fusion.py +108 -0
- models/backbone.py +234 -0
- models/bezier_control_point_estimator.py +90 -0
- models/color_naming.py +70 -0
- models/interactive_model.py +125 -0
- models/joost_color_naming.mat +3 -0
- models/model.py +28 -0
- output/a4957-input.png +0 -0
- requirements.txt +33 -0
- scripts/download_checkpoints.sh +9 -0
- scripts/generate_naming_maps.py +29 -0
- test.py +41 -0
- train.py +73 -0
- utils/deltaE.py +125 -0
- utils/evaluator.py +69 -0
- utils/logger.py +21 -0
- utils/setup_criterion.py +26 -0
- utils/setup_optim_scheduler.py +10 -0
- utils/trainer.py +47 -0
.gitattributes
CHANGED
|
@@ -33,3 +33,4 @@ saved_model/**/* filter=lfs diff=lfs merge=lfs -text
|
|
| 33 |
*.zip filter=lfs diff=lfs merge=lfs -text
|
| 34 |
*.zst filter=lfs diff=lfs merge=lfs -text
|
| 35 |
*tfevents* filter=lfs diff=lfs merge=lfs -text
|
|
|
|
|
|
| 33 |
*.zip filter=lfs diff=lfs merge=lfs -text
|
| 34 |
*.zst filter=lfs diff=lfs merge=lfs -text
|
| 35 |
*tfevents* filter=lfs diff=lfs merge=lfs -text
|
| 36 |
+
models/joost_color_naming.mat filter=lfs diff=lfs merge=lfs -text
|
README.md
CHANGED
|
@@ -1,14 +1,124 @@
|
|
| 1 |
-
|
| 2 |
-
|
| 3 |
-
|
| 4 |
-
|
| 5 |
-
|
| 6 |
-
|
| 7 |
-
|
| 8 |
-
|
| 9 |
-
|
| 10 |
-
|
| 11 |
-
|
| 12 |
-
|
| 13 |
-
|
| 14 |
-
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+

|
| 2 |
+
|
| 3 |
+
This repository is the official implementation of "NamedCurves: Learned Image Enhancement via Color Naming" @ ECCV24.
|
| 4 |
+
|
| 5 |
+
[](https://arxiv.org/abs/2407.09892)
|
| 6 |
+
[](https://namedcurves.github.io/)
|
| 7 |
+
|
| 8 |
+
[David Serrano-Lozano](https://davidserra9.github.io/), [Luis Herranz](http://www.lherranz.org/), [Michael S. Brown](http://www.cse.yorku.ca/~mbrown/) and [Javier Vazquez-Corral](https://www.jvazquez-corral.net/)
|
| 9 |
+
|
| 10 |
+
## News 🚀
|
| 11 |
+
- [Nov24] Code update. We release the inference images for MIT5K-UEGAN.
|
| 12 |
+
- [July24] We realease the code and pretrained models of our paper.
|
| 13 |
+
- [July24] Our paper NamedCurves is accepted to ECCV24!
|
| 14 |
+
|
| 15 |
+
## TODO:
|
| 16 |
+
- torch Dataset object for PPR10K
|
| 17 |
+
- Create notebook
|
| 18 |
+
- Create gradio demo
|
| 19 |
+
|
| 20 |
+
## Method
|
| 21 |
+
|
| 22 |
+
We propose NamedCurves, a learning-based image enhancement technique that decomposes the image into a small set of named colors. Our method learns to globally adjust the image for each specific named color via tone curves and then combines the images using and attention-based fusion mechanism to mimic spatial editing. In contrast to other SOTA methods, NamedCurves allows interpretability thanks to computing a set of tone curves for each universal color name.
|
| 23 |
+
|
| 24 |
+

|
| 25 |
+
|
| 26 |
+
## Data
|
| 27 |
+
|
| 28 |
+
In this paper we use two datasets: [MIT-Adobe FiveK](https://data.csail.mit.edu/graphics/fivek/) and [PPR10K](https://github.com/csjliang/PPR10K).
|
| 29 |
+
|
| 30 |
+
### MIT-Adobe FiveK
|
| 31 |
+
|
| 32 |
+
MIT FiveK dataset consists of 5,000 photographs taken by SLR cameras by a set of different photographers that cover a broad range of scenes, subjects, and lighting conditions. They are all in RAW format. Then, 5 different photography students adjust the tone of the photos. Each of them retouched all the 5,000 photos using Adobe Lightroom.
|
| 33 |
+
|
| 34 |
+
Following previous works we decided to use just the expert-C redition. To obtain the retouched images, we have to render the RAW files using Adobe Lightroom. Because of this, researchers have created different rendered versions of the dataset. In this paper, we use 3 different versions: DPE, UPE and UEGAN, dubbed after the method that introduced them. Some methods were evaluated in only some of the versions and their code and models are not available, so we considered it was fair to compare our results in the same conditions as they did. Now, we will provide information on the properties of each version and how to obtain them:
|
| 35 |
+
|
| 36 |
+
The dataset can be downloaded [here](ttps://data.csail.mit.edu/graphics/fivek/). After downloading the images you will need to use Adobe Lightroom to pre-process them according to each version.
|
| 37 |
+
|
| 38 |
+
- The **DPE** version uses the first 2,250 images of the dataset for training, the following 2,250 for validation and the last 500 for testing. The images are rendered to have the short edge to 512 pixels. Please see the [issue](https://github.com/sjmoran/CURL/issues/20) for detailed instructions.
|
| 39 |
+
|
| 40 |
+
- The **UPE** version uses the first 4,500 images of the dataset for training and the last 500 for testing. The images are rendered to have the short edge to 512 pixels. Please see the [issue](https://github.com/dvlab-research/DeepUPE/issues/26) for detailed instructions.
|
| 41 |
+
|
| 42 |
+
- The **UEGAN** version uses the first 4,500 images of the dataset for training and the last 500 for testing. The images are rendered to have the short edge to 512 pixels. For downloading the rendered images from [Google Drive](https://drive.google.com/drive/folders/1x-DcqFVoxprzM4KYGl8SUif8sV-57FP3). Please see the [official repository](https://github.com/dvlab-research/DeepUPE) for more information.
|
| 43 |
+
|
| 44 |
+
### PPR10K
|
| 45 |
+
PPR10K contains 1,681 high-quality RAW portraits photos manually retouched by 3 experts. The dataset can be downloaded from the [official repository](https://github.com/csjliang/PPR10K). We used the 480p images.
|
| 46 |
+
|
| 47 |
+
## Getting started
|
| 48 |
+
|
| 49 |
+
### Environment setup
|
| 50 |
+
|
| 51 |
+
We provide a Conda environment file ```requirements.txt``` with all necessary dependencies, except for PyTorch and Torchvision. Follow the instructions below to set up the environment.
|
| 52 |
+
|
| 53 |
+
First, create and activate the Conda environment:
|
| 54 |
+
|
| 55 |
+
```
|
| 56 |
+
conda create -n namedcurves python=3.8
|
| 57 |
+
conda activate namedcurves
|
| 58 |
+
```
|
| 59 |
+
|
| 60 |
+
Alternatively, you can set up a virtual environment:
|
| 61 |
+
```
|
| 62 |
+
python3 -m venv venv
|
| 63 |
+
source venv/bin/activate
|
| 64 |
+
```
|
| 65 |
+
|
| 66 |
+
Next, install PyTorch and Torchvision with the appropriate versions based on your CUDA and driver dependencies. Visit the [Pytorch Official Page](https://pytorch.org/get-started/previous-versions/) for specific installation commands. For example:
|
| 67 |
+
|
| 68 |
+
```
|
| 69 |
+
pip install torch==1.12.0+cu113 torchvision==0.13.0+cu113 --extra-index-url https://download.pytorch.org/whl/cu113
|
| 70 |
+
```
|
| 71 |
+
|
| 72 |
+
Once PyTorch is installed, you can install the remaining dependencies from the ```requirements.txt``` file:
|
| 73 |
+
|
| 74 |
+
```
|
| 75 |
+
pip install -r requirements.txt
|
| 76 |
+
```
|
| 77 |
+
|
| 78 |
+
Alternatively, you can manually install the required packages:
|
| 79 |
+
```
|
| 80 |
+
pip install omegaconf matplotlib scipy scikit-image lpips torchmetrics
|
| 81 |
+
```
|
| 82 |
+
|
| 83 |
+
### Results
|
| 84 |
+
|
| 85 |
+
We provide our results for the MIT5K dataset in the following format: aXXXX_Y_Z.png, where XXXX is the 4-digit file ID, Y is the PSNR value, and Z is the $\Delta E2000$ color difference of the image. All numeric values are rounded to two decimal places.
|
| 86 |
+
|
| 87 |
+
| | PSNR | SSIM | $\Delta E2000$ | Images |
|
| 88 |
+
| :-------- | :------: | :-------: | :--------------: | :-------: |
|
| 89 |
+
| MIT5K | 25.59 | 0.936 | 6.07 | [Link](https://cvcuab-my.sharepoint.com/:f:/g/personal/dserrano_cvc_uab_cat/EijObxqdogJHpNufwKKZE4ABI78-4iQnO78V2mHkzfs07A?e=tVTWAq)
|
| 90 |
+
|
| 91 |
+
### Pre-trained models
|
| 92 |
+
|
| 93 |
+
Create and store the pre-trained models in a folder inside the repository.
|
| 94 |
+
|
| 95 |
+
```
|
| 96 |
+
cd namedcurves
|
| 97 |
+
mkdir pretrained
|
| 98 |
+
```
|
| 99 |
+
|
| 100 |
+
The weights can be found [here](https://github.com/davidserra9/namedcurves/releases/tag/v1.0). Alternatively, you can run:
|
| 101 |
+
|
| 102 |
+
```
|
| 103 |
+
cd namedcurves
|
| 104 |
+
bash scripts/download_checkpoints.sh
|
| 105 |
+
```
|
| 106 |
+
|
| 107 |
+
|
| 108 |
+
## Inference
|
| 109 |
+
|
| 110 |
+
The following command takes an image file or a folder with images and saves the results in the specified directory.
|
| 111 |
+
|
| 112 |
+
```
|
| 113 |
+
python test.py --input_path assets/a4957-input.png --output_path output/ --config_path configs/mit5k_upe_config.yaml --model_path pretrained/mit5k_uegan_psnr_25.59.pth
|
| 114 |
+
```
|
| 115 |
+
|
| 116 |
+
## Training
|
| 117 |
+
|
| 118 |
+
Modify the configurations of the ```configs``` folders and run the following command:
|
| 119 |
+
|
| 120 |
+
```
|
| 121 |
+
python train.py --config configs/mit5k_upe_config.yaml
|
| 122 |
+
```
|
| 123 |
+
|
| 124 |
+
|
app.py
ADDED
|
@@ -0,0 +1,470 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
import argparse
|
| 2 |
+
from omegaconf import OmegaConf
|
| 3 |
+
import gradio as gr
|
| 4 |
+
from PIL import Image
|
| 5 |
+
import os
|
| 6 |
+
import torch
|
| 7 |
+
import numpy as np
|
| 8 |
+
import io
|
| 9 |
+
import yaml
|
| 10 |
+
from huggingface_hub import hf_hub_download
|
| 11 |
+
import matplotlib.pyplot as plt
|
| 12 |
+
#from gradio_imageslider import ImageSlider
|
| 13 |
+
|
| 14 |
+
## local code
|
| 15 |
+
from models.interactive_model import NamedCurves
|
| 16 |
+
|
| 17 |
+
def dict2namespace(config):
|
| 18 |
+
namespace = argparse.Namespace()
|
| 19 |
+
for key, value in config.items():
|
| 20 |
+
if isinstance(value, dict):
|
| 21 |
+
new_value = dict2namespace(value)
|
| 22 |
+
else:
|
| 23 |
+
new_value = value
|
| 24 |
+
setattr(namespace, key, new_value)
|
| 25 |
+
return namespace
|
| 26 |
+
|
| 27 |
+
def get_named_curves(control_points):
|
| 28 |
+
linspace = torch.linspace(0, 1, steps=101).unsqueeze(0).unsqueeze(2).repeat(1, 3, 1, 1).to(device)
|
| 29 |
+
outspace = model.bcpe.apply_cubic_bezier(linspace, control_points)
|
| 30 |
+
|
| 31 |
+
fig = plt.figure()
|
| 32 |
+
plt.plot(linspace[0, 0, :, 0].cpu().numpy(),outspace[0, 0, :, 0].cpu().numpy(), 'r')
|
| 33 |
+
plt.plot(linspace[0, 1, :, 0].cpu().numpy(), outspace[0, 1, :, 0].cpu().numpy(), 'g')
|
| 34 |
+
plt.plot(linspace[0, 2, :, 0].cpu().numpy(), outspace[0, 2, :, 0].cpu().numpy(), 'b')
|
| 35 |
+
|
| 36 |
+
plt.scatter(control_points[0, 0, :, 1].cpu().numpy(), control_points[0, 0, :, 0].cpu().numpy(), c='r', marker='x')
|
| 37 |
+
plt.scatter(control_points[0, 1, :, 1].cpu().numpy(), control_points[0, 1, :, 0].cpu().numpy(), c='g', marker='x')
|
| 38 |
+
plt.scatter(control_points[0, 2, :, 1].cpu().numpy(), control_points[0, 2, :, 0].cpu().numpy(), c='b', marker='x')
|
| 39 |
+
|
| 40 |
+
plt.xlim(0, 1)
|
| 41 |
+
plt.ylim(0, 1)
|
| 42 |
+
plt.grid()
|
| 43 |
+
|
| 44 |
+
img_buf = io.BytesIO()
|
| 45 |
+
plt.savefig(img_buf, format='png', bbox_inches='tight', dpi=300)
|
| 46 |
+
plt.close(fig)
|
| 47 |
+
return Image.open(img_buf)
|
| 48 |
+
|
| 49 |
+
hf_hub_download(repo_id="davidserra9/NamedCurves", filename="mit5k_uegan_psnr_25.59.pth", local_dir="./")
|
| 50 |
+
|
| 51 |
+
CONFIG = "configs/mit5k_upe_config.yaml"
|
| 52 |
+
model_pt = "mit5k_uegan_psnr_25.59.pth"
|
| 53 |
+
|
| 54 |
+
# parse config file
|
| 55 |
+
config = OmegaConf.load(CONFIG)
|
| 56 |
+
|
| 57 |
+
config = dict2namespace(config)
|
| 58 |
+
|
| 59 |
+
device = torch.device("cuda") if torch.cuda.is_available() else torch.device("cpu")
|
| 60 |
+
model = NamedCurves(config.model).to(device)
|
| 61 |
+
model.load_state_dict(torch.load(model_pt)["model_state_dict"])
|
| 62 |
+
|
| 63 |
+
def load_img(filename, norm=True,):
|
| 64 |
+
img = np.array(Image.open(filename).convert("RGB"))
|
| 65 |
+
if norm:
|
| 66 |
+
img = img / 255.
|
| 67 |
+
img = img.astype(np.float32)
|
| 68 |
+
return img
|
| 69 |
+
|
| 70 |
+
def process_img(image):
|
| 71 |
+
img = np.array(image)
|
| 72 |
+
img = img / 255.
|
| 73 |
+
img = img.astype(np.float32)
|
| 74 |
+
y = torch.tensor(img).permute(2,0,1).unsqueeze(0).to(device)
|
| 75 |
+
|
| 76 |
+
with torch.no_grad():
|
| 77 |
+
enhanced_img, control_points = model(y, return_curves=True)
|
| 78 |
+
|
| 79 |
+
img_curves = [get_named_curves(control_points_i) for control_points_i in control_points]
|
| 80 |
+
|
| 81 |
+
enhanced_img = enhanced_img.squeeze().permute(1,2,0).clamp_(0, 1).cpu().detach().numpy()
|
| 82 |
+
enhanced_img = np.clip(enhanced_img, 0. , 1.)
|
| 83 |
+
|
| 84 |
+
enhanced_img = (enhanced_img * 255.0).round().astype(np.uint8) # float32 to uint8
|
| 85 |
+
oby_points = control_points[0][0, :, :, 0].detach().cpu().numpy()
|
| 86 |
+
achr_points = control_points[1][0, :, :, 0].detach().cpu().numpy()
|
| 87 |
+
pp_points = control_points[2][0, :, :, 0].detach().cpu().numpy()
|
| 88 |
+
red_points = control_points[3][0, :, :, 0].detach().cpu().numpy()
|
| 89 |
+
green_points = control_points[4][0, :, :, 0].detach().cpu().numpy()
|
| 90 |
+
blue_points = control_points[5][0, :, :, 0].detach().cpu().numpy()
|
| 91 |
+
|
| 92 |
+
return img_curves[0], oby_points[0, 0], oby_points[1, 0], oby_points[2, 0], oby_points[0, 1], oby_points[1, 1], oby_points[2, 1], oby_points[0, 2], oby_points[1, 2], oby_points[2, 2], oby_points[0, 3], oby_points[1, 3], oby_points[2, 3], oby_points[0, 4], oby_points[1, 4], oby_points[2, 4], oby_points[0, 5], oby_points[1, 5], oby_points[2, 5], oby_points[0, 6], oby_points[1, 6], oby_points[2, 6], oby_points[0, 7], oby_points[1, 7], oby_points[2, 7], oby_points[0, 8], oby_points[1, 8], oby_points[2, 8], oby_points[0, 9], oby_points[1, 9], oby_points[2, 9], oby_points[0, 10], oby_points[1, 10], oby_points[2, 10], img_curves[1], achr_points[0, 0], achr_points[1, 0], achr_points[2, 0], achr_points[0, 1], achr_points[1, 1], achr_points[2, 1], achr_points[0, 2], achr_points[1, 2], achr_points[2, 2], achr_points[0, 3], achr_points[1, 3], achr_points[2, 3], achr_points[0, 4], achr_points[1, 4], achr_points[2, 4], achr_points[0, 5], achr_points[1, 5], achr_points[2, 5], achr_points[0, 6], achr_points[1, 6], achr_points[2, 6], achr_points[0, 7], achr_points[1, 7], achr_points[2, 7], achr_points[0, 8], achr_points[1, 8], achr_points[2, 8], achr_points[0, 9], achr_points[1, 9], achr_points[2, 9], achr_points[0, 10], achr_points[1, 10], achr_points[2, 10], img_curves[2], pp_points[0, 0], pp_points[1, 0], pp_points[2, 0], pp_points[0, 1], pp_points[1, 1], pp_points[2, 1], pp_points[0, 2], pp_points[1, 2], pp_points[2, 2], pp_points[0, 3], pp_points[1, 3], pp_points[2, 3], pp_points[0, 4], pp_points[1, 4], pp_points[2, 4], pp_points[0, 5], pp_points[1, 5], pp_points[2, 5], pp_points[0, 6], pp_points[1, 6], pp_points[2, 6], pp_points[0, 7], pp_points[1, 7], pp_points[2, 7], pp_points[0, 8], pp_points[1, 8], pp_points[2, 8], pp_points[0, 9], pp_points[1, 9], pp_points[2, 9], pp_points[0, 10], pp_points[1, 10], pp_points[2, 10], img_curves[3], red_points[0, 0], red_points[1, 0], red_points[2, 0], red_points[0, 1], red_points[1, 1], red_points[2, 1], red_points[0, 2], red_points[1, 2], red_points[2, 2], red_points[0, 3], red_points[1, 3], red_points[2, 3], red_points[0, 4], red_points[1, 4], red_points[2, 4], red_points[0, 5], red_points[1, 5], red_points[2, 5], red_points[0, 6], red_points[1, 6], red_points[2, 6], red_points[0, 7], red_points[1, 7], red_points[2, 7], red_points[0, 8], red_points[1, 8], red_points[2, 8], red_points[0, 9], red_points[1, 9], red_points[2, 9], red_points[0, 10], red_points[1, 10], red_points[2, 10], img_curves[4], green_points[0, 0], green_points[1, 0], green_points[2, 0], green_points[0, 1], green_points[1, 1], green_points[2, 1], green_points[0, 2], green_points[1, 2], green_points[2, 2], green_points[0, 3], green_points[1, 3], green_points[2, 3], green_points[0, 4], green_points[1, 4], green_points[2, 4], green_points[0, 5], green_points[1, 5], green_points[2, 5], green_points[0, 6], green_points[1, 6], green_points[2, 6], green_points[0, 7], green_points[1, 7], green_points[2, 7], green_points[0, 8], green_points[1, 8], green_points[2, 8], green_points[0, 9], green_points[1, 9], green_points[2, 9], green_points[0, 10], green_points[1, 10], green_points[2, 10], img_curves[5], blue_points[0, 0], blue_points[1, 0], blue_points[2, 0], blue_points[0, 1], blue_points[1, 1], blue_points[2, 1], blue_points[0, 2], blue_points[1, 2], blue_points[2, 2], blue_points[0, 3], blue_points[1, 3], blue_points[2, 3], blue_points[0, 4], blue_points[1, 4], blue_points[2, 4], blue_points[0, 5], blue_points[1, 5], blue_points[2, 5], blue_points[0, 6], blue_points[1, 6], blue_points[2, 6], blue_points[0, 7], blue_points[1, 7], blue_points[2, 7], blue_points[0, 8], blue_points[1, 8], blue_points[2, 8], blue_points[0, 9], blue_points[1, 9], blue_points[2, 9], blue_points[0, 10], blue_points[1, 10], blue_points[2, 10], Image.fromarray(enhanced_img)
|
| 93 |
+
|
| 94 |
+
def process_img_with_sliders(image, oby_red_p0, oby_green_p0, oby_blue_p0, oby_red_p1, oby_green_p1, oby_blue_p1, oby_red_p2, oby_green_p2, oby_blue_p2, oby_red_p3, oby_green_p3, oby_blue_p3, oby_red_p4, oby_green_p4, oby_blue_p4, oby_red_p5, oby_green_p5, oby_blue_p5, oby_red_p6, oby_green_p6, oby_blue_p6, oby_red_p7, oby_green_p7, oby_blue_p7, oby_red_p8, oby_green_p8, oby_blue_p8, oby_red_p9, oby_green_p9, oby_blue_p9, oby_red_p10, oby_green_p10, oby_blue_p10,
|
| 95 |
+
achro_red_p0, achro_green_p0, achro_blue_p0, achro_red_p1, achro_green_p1, achro_blue_p1, achro_red_p2, achro_green_p2, achro_blue_p2, achro_red_p3, achro_green_p3, achro_blue_p3, achro_red_p4, achro_green_p4, achro_blue_p4, achro_red_p5, achro_green_p5, achro_blue_p5, achro_red_p6, achro_green_p6, achro_blue_p6, achro_red_p7, achro_green_p7, achro_blue_p7, achro_red_p8, achro_green_p8, achro_blue_p8, achro_red_p9, achro_green_p9, achro_blue_p9, achro_red_p10, achro_green_p10, achro_blue_p10,
|
| 96 |
+
pp_red_p0, pp_green_p0, pp_blue_p0, pp_red_p1, pp_green_p1, pp_blue_p1, pp_red_p2, pp_green_p2, pp_blue_p2, pp_red_p3, pp_green_p3, pp_blue_p3, pp_red_p4, pp_green_p4, pp_blue_p4, pp_red_p5, pp_green_p5, pp_blue_p5, pp_red_p6, pp_green_p6, pp_blue_p6, pp_red_p7, pp_green_p7, pp_blue_p7, pp_red_p8, pp_green_p8, pp_blue_p8, pp_red_p9, pp_green_p9, pp_blue_p9, pp_red_p10, pp_green_p10, pp_blue_p10,
|
| 97 |
+
red_red_p0, red_green_p0, red_blue_p0, red_red_p1, red_green_p1, red_blue_p1, red_red_p2, red_green_p2, red_blue_p2, red_red_p3, red_green_p3, red_blue_p3, red_red_p4, red_green_p4, red_blue_p4, red_red_p5, red_green_p5, red_blue_p5, red_red_p6, red_green_p6, red_blue_p6, red_red_p7, red_green_p7, red_blue_p7, red_red_p8, red_green_p8, red_blue_p8, red_red_p9, red_green_p9, red_blue_p9, red_red_p10, red_green_p10, red_blue_p10,
|
| 98 |
+
green_red_p0, green_green_p0, green_blue_p0, green_red_p1, green_green_p1, green_blue_p1, green_red_p2, green_green_p2, green_blue_p2, green_red_p3, green_green_p3, green_blue_p3, green_red_p4, green_green_p4, green_blue_p4, green_red_p5, green_green_p5, green_blue_p5, green_red_p6, green_green_p6, green_blue_p6, green_red_p7, green_green_p7, green_blue_p7, green_red_p8, green_green_p8, green_blue_p8, green_red_p9, green_green_p9, green_blue_p9, green_red_p10, green_green_p10, green_blue_p10,
|
| 99 |
+
blue_red_p0, blue_green_p0, blue_blue_p0, blue_red_p1, blue_green_p1, blue_blue_p1, blue_red_p2, blue_green_p2, blue_blue_p2, blue_red_p3, blue_green_p3, blue_blue_p3, blue_red_p4, blue_green_p4, blue_blue_p4, blue_red_p5, blue_green_p5, blue_blue_p5, blue_red_p6, blue_green_p6, blue_blue_p6, blue_red_p7, blue_green_p7, blue_blue_p7, blue_red_p8, blue_green_p8, blue_blue_p8, blue_red_p9, blue_green_p9, blue_blue_p9, blue_red_p10, blue_green_p10, blue_blue_p10,
|
| 100 |
+
):
|
| 101 |
+
|
| 102 |
+
x = np.linspace(0, 1, 11)
|
| 103 |
+
oby_r_y = [float(oby_red_p0), float(oby_red_p1), float(oby_red_p2), float(oby_red_p3), float(oby_red_p4), float(oby_red_p5), float(oby_red_p6), float(oby_red_p7), float(oby_red_p8), float(oby_red_p9), float(oby_red_p10)]
|
| 104 |
+
oby_g_y = [float(oby_green_p0), float(oby_green_p1), float(oby_green_p2), float(oby_green_p3), float(oby_green_p4), float(oby_green_p5), float(oby_green_p6), float(oby_green_p7), float(oby_green_p8), float(oby_green_p9), float(oby_green_p10)]
|
| 105 |
+
oby_b_y = [float(oby_blue_p0), float(oby_blue_p1), float(oby_blue_p2), float(oby_blue_p3), float(oby_blue_p4), float(oby_blue_p5), float(oby_blue_p6), float(oby_blue_p7), float(oby_blue_p8), float(oby_blue_p9), float(oby_blue_p10)]
|
| 106 |
+
achro_r_y = [float(achro_red_p0), float(achro_red_p1), float(achro_red_p2), float(achro_red_p3), float(achro_red_p4), float(achro_red_p5), float(achro_red_p6), float(achro_red_p7), float(achro_red_p8), float(achro_red_p9), float(achro_red_p10)]
|
| 107 |
+
achro_g_y = [float(achro_green_p0), float(achro_green_p1), float(achro_green_p2), float(achro_green_p3), float(achro_green_p4), float(achro_green_p5), float(achro_green_p6), float(achro_green_p7), float(achro_green_p8), float(achro_green_p9), float(achro_green_p10)]
|
| 108 |
+
achro_b_y = [float(achro_blue_p0), float(achro_blue_p1), float(achro_blue_p2), float(achro_blue_p3), float(achro_blue_p4), float(achro_blue_p5), float(achro_blue_p6), float(achro_blue_p7), float(achro_blue_p8), float(achro_blue_p9), float(achro_blue_p10)]
|
| 109 |
+
pp_r_y = [float(pp_red_p0), float(pp_red_p1), float(pp_red_p2), float(pp_red_p3), float(pp_red_p4), float(pp_red_p5), float(pp_red_p6), float(pp_red_p7), float(pp_red_p8), float(pp_red_p9), float(pp_red_p10)]
|
| 110 |
+
pp_g_y = [float(pp_green_p0), float(pp_green_p1), float(pp_green_p2), float(pp_green_p3), float(pp_green_p4), float(pp_green_p5), float(pp_green_p6), float(pp_green_p7), float(pp_green_p8), float(pp_green_p9), float(pp_green_p10)]
|
| 111 |
+
pp_b_y = [float(pp_blue_p0), float(pp_blue_p1), float(pp_blue_p2), float(pp_blue_p3), float(pp_blue_p4), float(pp_blue_p5), float(pp_blue_p6), float(pp_blue_p7), float(pp_blue_p8), float(pp_blue_p9), float(pp_blue_p10)]
|
| 112 |
+
red_r_y = [float(red_red_p0), float(red_red_p1), float(red_red_p2), float(red_red_p3), float(red_red_p4), float(red_red_p5), float(red_red_p6), float(red_red_p7), float(red_red_p8), float(red_red_p9), float(red_red_p10)]
|
| 113 |
+
red_g_y = [float(red_green_p0), float(red_green_p1), float(red_green_p2), float(red_green_p3), float(red_green_p4), float(red_green_p5), float(red_green_p6), float(red_green_p7), float(red_green_p8), float(red_green_p9), float(red_green_p10)]
|
| 114 |
+
red_b_y = [float(red_blue_p0), float(red_blue_p1), float(red_blue_p2), float(red_blue_p3), float(red_blue_p4), float(red_blue_p5), float(red_blue_p6), float(red_blue_p7), float(red_blue_p8), float(red_blue_p9), float(red_blue_p10)]
|
| 115 |
+
green_r_y = [float(green_red_p0), float(green_red_p1), float(green_red_p2), float(green_red_p3), float(green_red_p4), float(green_red_p5), float(green_red_p6), float(green_red_p7), float(green_red_p8), float(green_red_p9), float(green_red_p10)]
|
| 116 |
+
green_g_y = [float(green_green_p0), float(green_green_p1), float(green_green_p2), float(green_green_p3), float(green_green_p4), float(green_green_p5), float(green_green_p6), float(green_green_p7), float(green_green_p8), float(green_green_p9), float(green_green_p10)]
|
| 117 |
+
green_b_y = [float(green_blue_p0), float(green_blue_p1), float(green_blue_p2), float(green_blue_p3), float(green_blue_p4), float(green_blue_p5), float(green_blue_p6), float(green_blue_p7), float(green_blue_p8), float(green_blue_p9), float(green_blue_p10)]
|
| 118 |
+
blue_r_y = [float(blue_red_p0), float(blue_red_p1), float(blue_red_p2), float(blue_red_p3), float(blue_red_p4), float(blue_red_p5), float(blue_red_p6), float(blue_red_p7), float(blue_red_p8), float(blue_red_p9), float(blue_red_p10)]
|
| 119 |
+
blue_g_y = [float(blue_green_p0), float(blue_green_p1), float(blue_green_p2), float(blue_green_p3), float(blue_green_p4), float(blue_green_p5), float(blue_green_p6), float(blue_green_p7), float(blue_green_p8), float(blue_green_p9), float(blue_green_p10)]
|
| 120 |
+
blue_b_y = [float(blue_blue_p0), float(blue_blue_p1), float(blue_blue_p2), float(blue_blue_p3), float(blue_blue_p4), float(blue_blue_p5), float(blue_blue_p6), float(blue_blue_p7), float(blue_blue_p8), float(blue_blue_p9), float(blue_blue_p10)]
|
| 121 |
+
|
| 122 |
+
oby_y = torch.concatenate([torch.tensor(np.array([oby_r_y, x]).T).unsqueeze(0), torch.tensor(np.array([oby_g_y, x]).T).unsqueeze(0), torch.tensor(np.array([oby_b_y, x]).T).unsqueeze(0)], dim=0).unsqueeze(0).to(device)
|
| 123 |
+
achro_y = torch.concatenate([torch.tensor(np.array([achro_r_y, x]).T).unsqueeze(0), torch.tensor(np.array([achro_g_y, x]).T).unsqueeze(0), torch.tensor(np.array([achro_b_y, x]).T).unsqueeze(0)], dim=0).unsqueeze(0).to(device)
|
| 124 |
+
pp_y = torch.concatenate([torch.tensor(np.array([pp_r_y, x]).T).unsqueeze(0), torch.tensor(np.array([pp_g_y, x]).T).unsqueeze(0), torch.tensor(np.array([pp_b_y, x]).T).unsqueeze(0)], dim=0).unsqueeze(0).to(device)
|
| 125 |
+
red_y = torch.concatenate([torch.tensor(np.array([red_r_y, x]).T).unsqueeze(0), torch.tensor(np.array([red_g_y, x]).T).unsqueeze(0), torch.tensor(np.array([red_b_y, x]).T).unsqueeze(0)], dim=0).unsqueeze(0).to(device)
|
| 126 |
+
green_y = torch.concatenate([torch.tensor(np.array([green_r_y, x]).T).unsqueeze(0), torch.tensor(np.array([green_g_y, x]).T).unsqueeze(0), torch.tensor(np.array([green_b_y, x]).T).unsqueeze(0)], dim=0).unsqueeze(0).to(device)
|
| 127 |
+
blue_y = torch.concatenate([torch.tensor(np.array([blue_r_y, x]).T).unsqueeze(0), torch.tensor(np.array([blue_g_y, x]).T).unsqueeze(0), torch.tensor(np.array([blue_b_y, x]).T).unsqueeze(0)], dim=0).unsqueeze(0).to(device)
|
| 128 |
+
|
| 129 |
+
control_points = [oby_y, achro_y, pp_y, red_y, green_y, blue_y]
|
| 130 |
+
|
| 131 |
+
img = np.array(image)
|
| 132 |
+
img = img / 255.
|
| 133 |
+
img = img.astype(np.float32)
|
| 134 |
+
y = torch.tensor(img).permute(2,0,1).unsqueeze(0).to(device)
|
| 135 |
+
|
| 136 |
+
with torch.no_grad():
|
| 137 |
+
enhanced_img, control_points = model(y, return_curves=True, control_points=control_points)
|
| 138 |
+
|
| 139 |
+
img_curves = [get_named_curves(control_points_i) for control_points_i in control_points]
|
| 140 |
+
|
| 141 |
+
enhanced_img = enhanced_img.squeeze().permute(1,2,0).clamp_(0, 1).cpu().detach().numpy()
|
| 142 |
+
enhanced_img = np.clip(enhanced_img, 0. , 1.)
|
| 143 |
+
|
| 144 |
+
enhanced_img = (enhanced_img * 255.0).round().astype(np.uint8) # float32 to uint8
|
| 145 |
+
oby_points = control_points[0][0, :, :, 0].detach().cpu().numpy()
|
| 146 |
+
achr_points = control_points[1][0, :, :, 0].detach().cpu().numpy()
|
| 147 |
+
pp_points = control_points[2][0, :, :, 0].detach().cpu().numpy()
|
| 148 |
+
red_points = control_points[3][0, :, :, 0].detach().cpu().numpy()
|
| 149 |
+
green_points = control_points[4][0, :, :, 0].detach().cpu().numpy()
|
| 150 |
+
blue_points = control_points[5][0, :, :, 0].detach().cpu().numpy()
|
| 151 |
+
|
| 152 |
+
return img_curves[0], oby_points[0, 0], oby_points[1, 0], oby_points[2, 0], oby_points[0, 1], oby_points[1, 1], oby_points[2, 1], oby_points[0, 2], oby_points[1, 2], oby_points[2, 2], oby_points[0, 3], oby_points[1, 3], oby_points[2, 3], oby_points[0, 4], oby_points[1, 4], oby_points[2, 4], oby_points[0, 5], oby_points[1, 5], oby_points[2, 5], oby_points[0, 6], oby_points[1, 6], oby_points[2, 6], oby_points[0, 7], oby_points[1, 7], oby_points[2, 7], oby_points[0, 8], oby_points[1, 8], oby_points[2, 8], oby_points[0, 9], oby_points[1, 9], oby_points[2, 9], oby_points[0, 10], oby_points[1, 10], oby_points[2, 10], img_curves[1], achr_points[0, 0], achr_points[1, 0], achr_points[2, 0], achr_points[0, 1], achr_points[1, 1], achr_points[2, 1], achr_points[0, 2], achr_points[1, 2], achr_points[2, 2], achr_points[0, 3], achr_points[1, 3], achr_points[2, 3], achr_points[0, 4], achr_points[1, 4], achr_points[2, 4], achr_points[0, 5], achr_points[1, 5], achr_points[2, 5], achr_points[0, 6], achr_points[1, 6], achr_points[2, 6], achr_points[0, 7], achr_points[1, 7], achr_points[2, 7], achr_points[0, 8], achr_points[1, 8], achr_points[2, 8], achr_points[0, 9], achr_points[1, 9], achr_points[2, 9], achr_points[0, 10], achr_points[1, 10], achr_points[2, 10], img_curves[2], pp_points[0, 0], pp_points[1, 0], pp_points[2, 0], pp_points[0, 1], pp_points[1, 1], pp_points[2, 1], pp_points[0, 2], pp_points[1, 2], pp_points[2, 2], pp_points[0, 3], pp_points[1, 3], pp_points[2, 3], pp_points[0, 4], pp_points[1, 4], pp_points[2, 4], pp_points[0, 5], pp_points[1, 5], pp_points[2, 5], pp_points[0, 6], pp_points[1, 6], pp_points[2, 6], pp_points[0, 7], pp_points[1, 7], pp_points[2, 7], pp_points[0, 8], pp_points[1, 8], pp_points[2, 8], pp_points[0, 9], pp_points[1, 9], pp_points[2, 9], pp_points[0, 10], pp_points[1, 10], pp_points[2, 10], img_curves[3], red_points[0, 0], red_points[1, 0], red_points[2, 0], red_points[0, 1], red_points[1, 1], red_points[2, 1], red_points[0, 2], red_points[1, 2], red_points[2, 2], red_points[0, 3], red_points[1, 3], red_points[2, 3], red_points[0, 4], red_points[1, 4], red_points[2, 4], red_points[0, 5], red_points[1, 5], red_points[2, 5], red_points[0, 6], red_points[1, 6], red_points[2, 6], red_points[0, 7], red_points[1, 7], red_points[2, 7], red_points[0, 8], red_points[1, 8], red_points[2, 8], red_points[0, 9], red_points[1, 9], red_points[2, 9], red_points[0, 10], red_points[1, 10], red_points[2, 10], img_curves[4], green_points[0, 0], green_points[1, 0], green_points[2, 0], green_points[0, 1], green_points[1, 1], green_points[2, 1], green_points[0, 2], green_points[1, 2], green_points[2, 2], green_points[0, 3], green_points[1, 3], green_points[2, 3], green_points[0, 4], green_points[1, 4], green_points[2, 4], green_points[0, 5], green_points[1, 5], green_points[2, 5], green_points[0, 6], green_points[1, 6], green_points[2, 6], green_points[0, 7], green_points[1, 7], green_points[2, 7], green_points[0, 8], green_points[1, 8], green_points[2, 8], green_points[0, 9], green_points[1, 9], green_points[2, 9], green_points[0, 10], green_points[1, 10], green_points[2, 10], img_curves[5], blue_points[0, 0], blue_points[1, 0], blue_points[2, 0], blue_points[0, 1], blue_points[1, 1], blue_points[2, 1], blue_points[0, 2], blue_points[1, 2], blue_points[2, 2], blue_points[0, 3], blue_points[1, 3], blue_points[2, 3], blue_points[0, 4], blue_points[1, 4], blue_points[2, 4], blue_points[0, 5], blue_points[1, 5], blue_points[2, 5], blue_points[0, 6], blue_points[1, 6], blue_points[2, 6], blue_points[0, 7], blue_points[1, 7], blue_points[2, 7], blue_points[0, 8], blue_points[1, 8], blue_points[2, 8], blue_points[0, 9], blue_points[1, 9], blue_points[2, 9], blue_points[0, 10], blue_points[1, 10], blue_points[2, 10], Image.fromarray(enhanced_img)
|
| 153 |
+
|
| 154 |
+
|
| 155 |
+
|
| 156 |
+
|
| 157 |
+
title = "NamedCurves🌈🤗"
|
| 158 |
+
description = '''
|
| 159 |
+
'''
|
| 160 |
+
|
| 161 |
+
article = "<p style='text-align: center'><a href='https://github.com/davidserra9/namedcurves' target='_blank'>NamedCurves: Learned Image Enhancement via Color Naming</a></p>"
|
| 162 |
+
|
| 163 |
+
#### Image,Prompts examples
|
| 164 |
+
#examples = [['assets/a4957-input.png']]
|
| 165 |
+
|
| 166 |
+
css = """
|
| 167 |
+
.image-frame img, .image-container img {
|
| 168 |
+
width: auto;
|
| 169 |
+
height: auto;
|
| 170 |
+
max-width: none;
|
| 171 |
+
}
|
| 172 |
+
"""
|
| 173 |
+
|
| 174 |
+
with gr.Blocks() as demo:
|
| 175 |
+
gr.Markdown("""
|
| 176 |
+
## [NamedCurves](https://namedcurves.github.io/): Learned Image Enhancement via Color Naming
|
| 177 |
+
[David Serrano-Lozano](https://davidserra9.github.io/), [Luis Herranz](https://www.lherranz.org/), [Michael S. Brown](https://www.eecs.yorku.ca/~mbrown/), [Javier Vazquez-Corral](https://jvazquezcorral.github.io/)
|
| 178 |
+
Computer Vision Center, Universitat Autònoma de Barcelona, Universidad Autónoma de Madrid, York University
|
| 179 |
+
|
| 180 |
+
**NamedCurves decomposes an image into a small set of named colors and enhances them using a learned set of tone curves.** By making this decomposition, we improve the interactivity of the model as the user can modify the tone curves assigned to color name to manipulate only a certain color of the image.
|
| 181 |
+
|
| 182 |
+
* Upload an image and click "Run" to automatically enhance the image.
|
| 183 |
+
* Then, you can adjust the tone curves for each color name to make the retouched version to your liking. Manipulate the sliders corresponding to the control points that define the tone curves. Note that for simplicity, we show the intensity values of the control points instead of the RGB values of each control point.
|
| 184 |
+
|
| 185 |
+
""")
|
| 186 |
+
with gr.Row():
|
| 187 |
+
with gr.Column():
|
| 188 |
+
image = gr.Image(type="pil", label="Input")
|
| 189 |
+
run_btn = gr.Button("Run")
|
| 190 |
+
examples = gr.Examples(['assets/a4957-input.png', 'assets/a4996-input.png', 'assets/a4998-input.png', 'assets/a5000-input.png',
|
| 191 |
+
'assets/a4986-input.png', 'assets/a4988-input.png', 'assets/a4990-input.png', 'assets/a4993-input.png'], inputs=[image])
|
| 192 |
+
|
| 193 |
+
with gr.Tabs() as input_tabs:
|
| 194 |
+
with gr.Tab(label="Orange", id=0) as oby_curves_tab:
|
| 195 |
+
oby_curves = gr.Image(label="Orange-Brown-Yellow Curves", type="pil")
|
| 196 |
+
with gr.Tabs() as channel_tabs:
|
| 197 |
+
with gr.Tab(label="R", id=0) as oby_red_curves_tab:
|
| 198 |
+
oby_red_p0 = gr.Slider(0, 1, label="R-P0", interactive=True)
|
| 199 |
+
oby_red_p1 = gr.Slider(0, 1, label="R-P1", interactive=True)
|
| 200 |
+
oby_red_p2 = gr.Slider(0, 1, label="R-P2", interactive=True)
|
| 201 |
+
oby_red_p3 = gr.Slider(0, 1, label="R-P3", interactive=True)
|
| 202 |
+
oby_red_p4 = gr.Slider(0, 1, label="R-P4", interactive=True)
|
| 203 |
+
oby_red_p5 = gr.Slider(0, 1, label="R-P5", interactive=True)
|
| 204 |
+
oby_red_p6 = gr.Slider(0, 1, label="R-P6", interactive=True)
|
| 205 |
+
oby_red_p7 = gr.Slider(0, 1, label="R-P7", interactive=True)
|
| 206 |
+
oby_red_p8 = gr.Slider(0, 1, label="R-P8", interactive=True)
|
| 207 |
+
oby_red_p9 = gr.Slider(0, 1, label="R-P9", interactive=True)
|
| 208 |
+
oby_red_p10 = gr.Slider(0, 1, label="R-P10", interactive=True)
|
| 209 |
+
with gr.Tab(label="G", id=1) as oby_green_curves_tab:
|
| 210 |
+
oby_green_p0 = gr.Slider(0, 1, label="G-P0", interactive=True)
|
| 211 |
+
oby_green_p1 = gr.Slider(0, 1, label="G-P1", interactive=True)
|
| 212 |
+
oby_green_p2 = gr.Slider(0, 1, label="G-P2", interactive=True)
|
| 213 |
+
oby_green_p3 = gr.Slider(0, 1, label="G-P3", interactive=True)
|
| 214 |
+
oby_green_p4 = gr.Slider(0, 1, label="G-P4", interactive=True)
|
| 215 |
+
oby_green_p5 = gr.Slider(0, 1, label="G-P5", interactive=True)
|
| 216 |
+
oby_green_p6 = gr.Slider(0, 1, label="G-P6", interactive=True)
|
| 217 |
+
oby_green_p7 = gr.Slider(0, 1, label="G-P7", interactive=True)
|
| 218 |
+
oby_green_p8 = gr.Slider(0, 1, label="G-P8", interactive=True)
|
| 219 |
+
oby_green_p9 = gr.Slider(0, 1, label="G-P9", interactive=True)
|
| 220 |
+
oby_green_p10 = gr.Slider(0, 1, label="G-P10", interactive=True)
|
| 221 |
+
with gr.Tab(label="B", id=2) as oby_blue_curves_tab:
|
| 222 |
+
oby_blue_p0 = gr.Slider(0, 1, label="B-P0", interactive=True)
|
| 223 |
+
oby_blue_p1 = gr.Slider(0, 1, label="B-P1", interactive=True)
|
| 224 |
+
oby_blue_p2 = gr.Slider(0, 1, label="B-P2", interactive=True)
|
| 225 |
+
oby_blue_p3 = gr.Slider(0, 1, label="B-P3", interactive=True)
|
| 226 |
+
oby_blue_p4 = gr.Slider(0, 1, label="B-P4", interactive=True)
|
| 227 |
+
oby_blue_p5 = gr.Slider(0, 1, label="B-P5", interactive=True)
|
| 228 |
+
oby_blue_p6 = gr.Slider(0, 1, label="B-P6", interactive=True)
|
| 229 |
+
oby_blue_p7 = gr.Slider(0, 1, label="B-P7", interactive=True)
|
| 230 |
+
oby_blue_p8 = gr.Slider(0, 1, label="B-P8", interactive=True)
|
| 231 |
+
oby_blue_p9 = gr.Slider(0, 1, label="B-P9", interactive=True)
|
| 232 |
+
oby_blue_p10 = gr.Slider(0, 1, label="B-P10", interactive=True)
|
| 233 |
+
|
| 234 |
+
with gr.Tab(label="Achr", id=1) as achro_curves_tab:
|
| 235 |
+
achro_curves = gr.Image(label="Achromatic Curves", type="pil")
|
| 236 |
+
with gr.Tabs() as channel_tabs:
|
| 237 |
+
with gr.Tab(label="R", id=0) as achro_red_curves_tab:
|
| 238 |
+
achro_red_p0 = gr.Slider(0, 1, label="R-P0", interactive=True)
|
| 239 |
+
achro_red_p1 = gr.Slider(0, 1, label="R-P1", interactive=True)
|
| 240 |
+
achro_red_p2 = gr.Slider(0, 1, label="R-P2", interactive=True)
|
| 241 |
+
achro_red_p3 = gr.Slider(0, 1, label="R-P3", interactive=True)
|
| 242 |
+
achro_red_p4 = gr.Slider(0, 1, label="R-P4", interactive=True)
|
| 243 |
+
achro_red_p5 = gr.Slider(0, 1, label="R-P5", interactive=True)
|
| 244 |
+
achro_red_p6 = gr.Slider(0, 1, label="R-P6", interactive=True)
|
| 245 |
+
achro_red_p7 = gr.Slider(0, 1, label="R-P7", interactive=True)
|
| 246 |
+
achro_red_p8 = gr.Slider(0, 1, label="R-P8", interactive=True)
|
| 247 |
+
achro_red_p9 = gr.Slider(0, 1, label="R-P9", interactive=True)
|
| 248 |
+
achro_red_p10 = gr.Slider(0, 1, label="R-P10", interactive=True)
|
| 249 |
+
with gr.Tab(label="G", id=1) as achro_green_curves_tab:
|
| 250 |
+
achro_green_p0 = gr.Slider(0, 1, label="G-P0", interactive=True)
|
| 251 |
+
achro_green_p1 = gr.Slider(0, 1, label="G-P1", interactive=True)
|
| 252 |
+
achro_green_p2 = gr.Slider(0, 1, label="G-P2", interactive=True)
|
| 253 |
+
achro_green_p3 = gr.Slider(0, 1, label="G-P3", interactive=True)
|
| 254 |
+
achro_green_p4 = gr.Slider(0, 1, label="G-P4", interactive=True)
|
| 255 |
+
achro_green_p5 = gr.Slider(0, 1, label="G-P5", interactive=True)
|
| 256 |
+
achro_green_p6 = gr.Slider(0, 1, label="G-P6", interactive=True)
|
| 257 |
+
achro_green_p7 = gr.Slider(0, 1, label="G-P7", interactive=True)
|
| 258 |
+
achro_green_p8 = gr.Slider(0, 1, label="G-P8", interactive=True)
|
| 259 |
+
achro_green_p9 = gr.Slider(0, 1, label="G-P9", interactive=True)
|
| 260 |
+
achro_green_p10 = gr.Slider(0, 1, label="G-P10", interactive=True)
|
| 261 |
+
with gr.Tab(label="B", id=2) as achro_blue_curves_tab:
|
| 262 |
+
achro_blue_p0 = gr.Slider(0, 1, label="B-P0", interactive=True)
|
| 263 |
+
achro_blue_p1 = gr.Slider(0, 1, label="B-P1", interactive=True)
|
| 264 |
+
achro_blue_p2 = gr.Slider(0, 1, label="B-P2", interactive=True)
|
| 265 |
+
achro_blue_p3 = gr.Slider(0, 1, label="B-P3", interactive=True)
|
| 266 |
+
achro_blue_p4 = gr.Slider(0, 1, label="B-P4", interactive=True)
|
| 267 |
+
achro_blue_p5 = gr.Slider(0, 1, label="B-P5", interactive=True)
|
| 268 |
+
achro_blue_p6 = gr.Slider(0, 1, label="B-P6", interactive=True)
|
| 269 |
+
achro_blue_p7 = gr.Slider(0, 1, label="B-P7", interactive=True)
|
| 270 |
+
achro_blue_p8 = gr.Slider(0, 1, label="B-P8", interactive=True)
|
| 271 |
+
achro_blue_p9 = gr.Slider(0, 1, label="B-P9", interactive=True)
|
| 272 |
+
achro_blue_p10 = gr.Slider(0, 1, label="B-P10", interactive=True)
|
| 273 |
+
|
| 274 |
+
with gr.Tab(label="Pink", id=2) as pink_purple_curves_tab:
|
| 275 |
+
pink_purple_curves = gr.Image(label="Pink-Purple Curves", type="pil")
|
| 276 |
+
with gr.Tabs() as channel_tabs:
|
| 277 |
+
with gr.Tab(label="R", id=0) as pp_red_curves_tab:
|
| 278 |
+
pp_red_p0 = gr.Slider(0, 1, label="R-P0", interactive=True)
|
| 279 |
+
pp_red_p1 = gr.Slider(0, 1, label="R-P1", interactive=True)
|
| 280 |
+
pp_red_p2 = gr.Slider(0, 1, label="R-P2", interactive=True)
|
| 281 |
+
pp_red_p3 = gr.Slider(0, 1, label="R-P3", interactive=True)
|
| 282 |
+
pp_red_p4 = gr.Slider(0, 1, label="R-P4", interactive=True)
|
| 283 |
+
pp_red_p5 = gr.Slider(0, 1, label="R-P5", interactive=True)
|
| 284 |
+
pp_red_p6 = gr.Slider(0, 1, label="R-P6", interactive=True)
|
| 285 |
+
pp_red_p7 = gr.Slider(0, 1, label="R-P7", interactive=True)
|
| 286 |
+
pp_red_p8 = gr.Slider(0, 1, label="R-P8", interactive=True)
|
| 287 |
+
pp_red_p9 = gr.Slider(0, 1, label="R-P9", interactive=True)
|
| 288 |
+
pp_red_p10 = gr.Slider(0, 1, label="R-P10", interactive=True)
|
| 289 |
+
with gr.Tab(label="G", id=1) as pp_green_curves_tab:
|
| 290 |
+
pp_green_p0 = gr.Slider(0, 1, label="G-P0", interactive=True)
|
| 291 |
+
pp_green_p1 = gr.Slider(0, 1, label="G-P1", interactive=True)
|
| 292 |
+
pp_green_p2 = gr.Slider(0, 1, label="G-P2", interactive=True)
|
| 293 |
+
pp_green_p3 = gr.Slider(0, 1, label="G-P3", interactive=True)
|
| 294 |
+
pp_green_p4 = gr.Slider(0, 1, label="G-P4", interactive=True)
|
| 295 |
+
pp_green_p5 = gr.Slider(0, 1, label="G-P5", interactive=True)
|
| 296 |
+
pp_green_p6 = gr.Slider(0, 1, label="G-P6", interactive=True)
|
| 297 |
+
pp_green_p7 = gr.Slider(0, 1, label="G-P7", interactive=True)
|
| 298 |
+
pp_green_p8 = gr.Slider(0, 1, label="G-P8", interactive=True)
|
| 299 |
+
pp_green_p9 = gr.Slider(0, 1, label="G-P9", interactive=True)
|
| 300 |
+
pp_green_p10 = gr.Slider(0, 1, label="G-P10", interactive=True)
|
| 301 |
+
with gr.Tab(label="B", id=2) as pp_blue_curves_tab:
|
| 302 |
+
pp_blue_p0 = gr.Slider(0, 1, label="B-P0", interactive=True)
|
| 303 |
+
pp_blue_p1 = gr.Slider(0, 1, label="B-P1", interactive=True)
|
| 304 |
+
pp_blue_p2 = gr.Slider(0, 1, label="B-P2", interactive=True)
|
| 305 |
+
pp_blue_p3 = gr.Slider(0, 1, label="B-P3", interactive=True)
|
| 306 |
+
pp_blue_p4 = gr.Slider(0, 1, label="B-P4", interactive=True)
|
| 307 |
+
pp_blue_p5 = gr.Slider(0, 1, label="B-P5", interactive=True)
|
| 308 |
+
pp_blue_p6 = gr.Slider(0, 1, label="B-P6", interactive=True)
|
| 309 |
+
pp_blue_p7 = gr.Slider(0, 1, label="B-P7", interactive=True)
|
| 310 |
+
pp_blue_p8 = gr.Slider(0, 1, label="B-P8", interactive=True)
|
| 311 |
+
pp_blue_p9 = gr.Slider(0, 1, label="B-P9", interactive=True)
|
| 312 |
+
pp_blue_p10 = gr.Slider(0, 1, label="B-P10", interactive=True)
|
| 313 |
+
|
| 314 |
+
with gr.Tab(label="Red", id=3) as red_curves_tab:
|
| 315 |
+
red_curves = gr.Image(label="Red Curves", type="pil")
|
| 316 |
+
with gr.Tabs() as channel_tabs:
|
| 317 |
+
with gr.Tab(label="R", id=0) as red_red_curves_tab:
|
| 318 |
+
red_red_p0 = gr.Slider(0, 1, label="R-P0", interactive=True)
|
| 319 |
+
red_red_p1 = gr.Slider(0, 1, label="R-P1", interactive=True)
|
| 320 |
+
red_red_p2 = gr.Slider(0, 1, label="R-P2", interactive=True)
|
| 321 |
+
red_red_p3 = gr.Slider(0, 1, label="R-P3", interactive=True)
|
| 322 |
+
red_red_p4 = gr.Slider(0, 1, label="R-P4", interactive=True)
|
| 323 |
+
red_red_p5 = gr.Slider(0, 1, label="R-P5", interactive=True)
|
| 324 |
+
red_red_p6 = gr.Slider(0, 1, label="R-P6", interactive=True)
|
| 325 |
+
red_red_p7 = gr.Slider(0, 1, label="R-P7", interactive=True)
|
| 326 |
+
red_red_p8 = gr.Slider(0, 1, label="R-P8", interactive=True)
|
| 327 |
+
red_red_p9 = gr.Slider(0, 1, label="R-P9", interactive=True)
|
| 328 |
+
red_red_p10 = gr.Slider(0, 1, label="R-P10", interactive=True)
|
| 329 |
+
with gr.Tab(label="G", id=1) as red_green_curves_tab:
|
| 330 |
+
red_green_p0 = gr.Slider(0, 1, label="G-P0", interactive=True)
|
| 331 |
+
red_green_p1 = gr.Slider(0, 1, label="G-P1", interactive=True)
|
| 332 |
+
red_green_p2 = gr.Slider(0, 1, label="G-P2", interactive=True)
|
| 333 |
+
red_green_p3 = gr.Slider(0, 1, label="G-P3", interactive=True)
|
| 334 |
+
red_green_p4 = gr.Slider(0, 1, label="G-P4", interactive=True)
|
| 335 |
+
red_green_p5 = gr.Slider(0, 1, label="G-P5", interactive=True)
|
| 336 |
+
red_green_p6 = gr.Slider(0, 1, label="G-P6", interactive=True)
|
| 337 |
+
red_green_p7 = gr.Slider(0, 1, label="G-P7", interactive=True)
|
| 338 |
+
red_green_p8 = gr.Slider(0, 1, label="G-P8", interactive=True)
|
| 339 |
+
red_green_p9 = gr.Slider(0, 1, label="G-P9", interactive=True)
|
| 340 |
+
red_green_p10 = gr.Slider(0, 1, label="G-P10", interactive=True)
|
| 341 |
+
with gr.Tab(label="B", id=2) as red_blue_curves_tab:
|
| 342 |
+
red_blue_p0 = gr.Slider(0, 1, label="B-P0", interactive=True)
|
| 343 |
+
red_blue_p1 = gr.Slider(0, 1, label="B-P1", interactive=True)
|
| 344 |
+
red_blue_p2 = gr.Slider(0, 1, label="B-P2", interactive=True)
|
| 345 |
+
red_blue_p3 = gr.Slider(0, 1, label="B-P3", interactive=True)
|
| 346 |
+
red_blue_p4 = gr.Slider(0, 1, label="B-P4", interactive=True)
|
| 347 |
+
red_blue_p5 = gr.Slider(0, 1, label="B-P5", interactive=True)
|
| 348 |
+
red_blue_p6 = gr.Slider(0, 1, label="B-P6", interactive=True)
|
| 349 |
+
red_blue_p7 = gr.Slider(0, 1, label="B-P7", interactive=True)
|
| 350 |
+
red_blue_p8 = gr.Slider(0, 1, label="B-P8", interactive=True)
|
| 351 |
+
red_blue_p9 = gr.Slider(0, 1, label="B-P9", interactive=True)
|
| 352 |
+
red_blue_p10 = gr.Slider(0, 1, label="B-P10", interactive=True)
|
| 353 |
+
|
| 354 |
+
with gr.Tab(label="Green", id=4) as green_curves_tab:
|
| 355 |
+
green_curves = gr.Image(label="Green Curves", type="pil")
|
| 356 |
+
with gr.Tabs() as channel_tabs:
|
| 357 |
+
with gr.Tab(label="R", id=0) as green_red_curves_tab:
|
| 358 |
+
green_red_p0 = gr.Slider(0, 1, label="R-P0", interactive=True)
|
| 359 |
+
green_red_p1 = gr.Slider(0, 1, label="R-P1", interactive=True)
|
| 360 |
+
green_red_p2 = gr.Slider(0, 1, label="R-P2", interactive=True)
|
| 361 |
+
green_red_p3 = gr.Slider(0, 1, label="R-P3", interactive=True)
|
| 362 |
+
green_red_p4 = gr.Slider(0, 1, label="R-P4", interactive=True)
|
| 363 |
+
green_red_p5 = gr.Slider(0, 1, label="R-P5", interactive=True)
|
| 364 |
+
green_red_p6 = gr.Slider(0, 1, label="R-P6", interactive=True)
|
| 365 |
+
green_red_p7 = gr.Slider(0, 1, label="R-P7", interactive=True)
|
| 366 |
+
green_red_p8 = gr.Slider(0, 1, label="R-P8", interactive=True)
|
| 367 |
+
green_red_p9 = gr.Slider(0, 1, label="R-P9", interactive=True)
|
| 368 |
+
green_red_p10 = gr.Slider(0, 1, label="R-P10", interactive=True)
|
| 369 |
+
with gr.Tab(label="G", id=1) as green_green_curves_tab:
|
| 370 |
+
green_green_p0 = gr.Slider(0, 1, label="G-P0", interactive=True)
|
| 371 |
+
green_green_p1 = gr.Slider(0, 1, label="G-P1", interactive=True)
|
| 372 |
+
green_green_p2 = gr.Slider(0, 1, label="G-P2", interactive=True)
|
| 373 |
+
green_green_p3 = gr.Slider(0, 1, label="G-P3", interactive=True)
|
| 374 |
+
green_green_p4 = gr.Slider(0, 1, label="G-P4", interactive=True)
|
| 375 |
+
green_green_p5 = gr.Slider(0, 1, label="G-P5", interactive=True)
|
| 376 |
+
green_green_p6 = gr.Slider(0, 1, label="G-P6", interactive=True)
|
| 377 |
+
green_green_p7 = gr.Slider(0, 1, label="G-P7", interactive=True)
|
| 378 |
+
green_green_p8 = gr.Slider(0, 1, label="G-P8", interactive=True)
|
| 379 |
+
green_green_p9 = gr.Slider(0, 1, label="G-P9", interactive=True)
|
| 380 |
+
green_green_p10 = gr.Slider(0, 1, label="G-P10", interactive=True)
|
| 381 |
+
with gr.Tab(label="B", id=2) as green_blue_curves_tab:
|
| 382 |
+
green_blue_p0 = gr.Slider(0, 1, label="B-P0", interactive=True)
|
| 383 |
+
green_blue_p1 = gr.Slider(0, 1, label="B-P1", interactive=True)
|
| 384 |
+
green_blue_p2 = gr.Slider(0, 1, label="B-P2", interactive=True)
|
| 385 |
+
green_blue_p3 = gr.Slider(0, 1, label="B-P3", interactive=True)
|
| 386 |
+
green_blue_p4 = gr.Slider(0, 1, label="B-P4", interactive=True)
|
| 387 |
+
green_blue_p5 = gr.Slider(0, 1, label="B-P5", interactive=True)
|
| 388 |
+
green_blue_p6 = gr.Slider(0, 1, label="B-P6", interactive=True)
|
| 389 |
+
green_blue_p7 = gr.Slider(0, 1, label="B-P7", interactive=True)
|
| 390 |
+
green_blue_p8 = gr.Slider(0, 1, label="B-P8", interactive=True)
|
| 391 |
+
green_blue_p9 = gr.Slider(0, 1, label="B-P9", interactive=True)
|
| 392 |
+
green_blue_p10 = gr.Slider(0, 1, label="B-P10", interactive=True)
|
| 393 |
+
|
| 394 |
+
with gr.Tab(label="Blue", id=5) as blue_curves_tab:
|
| 395 |
+
blue_curves = gr.Image(label="Blue Curves", type="pil")
|
| 396 |
+
with gr.Tabs() as channel_tabs:
|
| 397 |
+
with gr.Tab(label="R", id=0) as blue_red_curves_tab:
|
| 398 |
+
blue_red_p0 = gr.Slider(0, 1, label="R-P0", interactive=True)
|
| 399 |
+
blue_red_p1 = gr.Slider(0, 1, label="R-P1", interactive=True)
|
| 400 |
+
blue_red_p2 = gr.Slider(0, 1, label="R-P2", interactive=True)
|
| 401 |
+
blue_red_p3 = gr.Slider(0, 1, label="R-P3", interactive=True)
|
| 402 |
+
blue_red_p4 = gr.Slider(0, 1, label="R-P4", interactive=True)
|
| 403 |
+
blue_red_p5 = gr.Slider(0, 1, label="R-P5", interactive=True)
|
| 404 |
+
blue_red_p6 = gr.Slider(0, 1, label="R-P6", interactive=True)
|
| 405 |
+
blue_red_p7 = gr.Slider(0, 1, label="R-P7", interactive=True)
|
| 406 |
+
blue_red_p8 = gr.Slider(0, 1, label="R-P8", interactive=True)
|
| 407 |
+
blue_red_p9 = gr.Slider(0, 1, label="R-P9", interactive=True)
|
| 408 |
+
blue_red_p10 = gr.Slider(0, 1, label="R-P10", interactive=True)
|
| 409 |
+
with gr.Tab(label="G", id=1) as blue_green_curves_tab:
|
| 410 |
+
blue_green_p0 = gr.Slider(0, 1, label="G-P0", interactive=True)
|
| 411 |
+
blue_green_p1 = gr.Slider(0, 1, label="G-P1", interactive=True)
|
| 412 |
+
blue_green_p2 = gr.Slider(0, 1, label="G-P2", interactive=True)
|
| 413 |
+
blue_green_p3 = gr.Slider(0, 1, label="G-P3", interactive=True)
|
| 414 |
+
blue_green_p4 = gr.Slider(0, 1, label="G-P4", interactive=True)
|
| 415 |
+
blue_green_p5 = gr.Slider(0, 1, label="G-P5", interactive=True)
|
| 416 |
+
blue_green_p6 = gr.Slider(0, 1, label="G-P6", interactive=True)
|
| 417 |
+
blue_green_p7 = gr.Slider(0, 1, label="G-P7", interactive=True)
|
| 418 |
+
blue_green_p8 = gr.Slider(0, 1, label="G-P8", interactive=True)
|
| 419 |
+
blue_green_p9 = gr.Slider(0, 1, label="G-P9", interactive=True)
|
| 420 |
+
blue_green_p10 = gr.Slider(0, 1, label="G-P10", interactive=True)
|
| 421 |
+
with gr.Tab(label="B", id=2) as blue_blue_curves_tab:
|
| 422 |
+
blue_blue_p0 = gr.Slider(0, 1, label="B-P0", interactive=True)
|
| 423 |
+
blue_blue_p1 = gr.Slider(0, 1, label="B-P1", interactive=True)
|
| 424 |
+
blue_blue_p2 = gr.Slider(0, 1, label="B-P2", interactive=True)
|
| 425 |
+
blue_blue_p3 = gr.Slider(0, 1, label="B-P3", interactive=True)
|
| 426 |
+
blue_blue_p4 = gr.Slider(0, 1, label="B-P4", interactive=True)
|
| 427 |
+
blue_blue_p5 = gr.Slider(0, 1, label="B-P5", interactive=True)
|
| 428 |
+
blue_blue_p6 = gr.Slider(0, 1, label="B-P6", interactive=True)
|
| 429 |
+
blue_blue_p7 = gr.Slider(0, 1, label="B-P7", interactive=True)
|
| 430 |
+
blue_blue_p8 = gr.Slider(0, 1, label="B-P8", interactive=True)
|
| 431 |
+
blue_blue_p9 = gr.Slider(0, 1, label="B-P9", interactive=True)
|
| 432 |
+
blue_blue_p10 = gr.Slider(0, 1, label="B-P10", interactive=True)
|
| 433 |
+
|
| 434 |
+
with gr.Column():
|
| 435 |
+
out_image = gr.Image(type="pil", label="Output")
|
| 436 |
+
recompute_btn = gr.Button("Recompute")
|
| 437 |
+
|
| 438 |
+
|
| 439 |
+
run_btn.click(
|
| 440 |
+
process_img,
|
| 441 |
+
inputs=[image],
|
| 442 |
+
outputs=[oby_curves, oby_red_p0, oby_green_p0, oby_blue_p0, oby_red_p1, oby_green_p1, oby_blue_p1, oby_red_p2, oby_green_p2, oby_blue_p2, oby_red_p3, oby_green_p3, oby_blue_p3, oby_red_p4, oby_green_p4, oby_blue_p4, oby_red_p5, oby_green_p5, oby_blue_p5, oby_red_p6, oby_green_p6, oby_blue_p6, oby_red_p7, oby_green_p7, oby_blue_p7, oby_red_p8, oby_green_p8, oby_blue_p8, oby_red_p9, oby_green_p9, oby_blue_p9, oby_red_p10, oby_green_p10, oby_blue_p10,
|
| 443 |
+
achro_curves, achro_red_p0, achro_green_p0, achro_blue_p0, achro_red_p1, achro_green_p1, achro_blue_p1, achro_red_p2, achro_green_p2, achro_blue_p2, achro_red_p3, achro_green_p3, achro_blue_p3, achro_red_p4, achro_green_p4, achro_blue_p4, achro_red_p5, achro_green_p5, achro_blue_p5, achro_red_p6, achro_green_p6, achro_blue_p6, achro_red_p7, achro_green_p7, achro_blue_p7, achro_red_p8, achro_green_p8, achro_blue_p8, achro_red_p9, achro_green_p9, achro_blue_p9, achro_red_p10, achro_green_p10, achro_blue_p10,
|
| 444 |
+
pink_purple_curves, pp_red_p0, pp_green_p0, pp_blue_p0, pp_red_p1, pp_green_p1, pp_blue_p1, pp_red_p2, pp_green_p2, pp_blue_p2, pp_red_p3, pp_green_p3, pp_blue_p3, pp_red_p4, pp_green_p4, pp_blue_p4, pp_red_p5, pp_green_p5, pp_blue_p5, pp_red_p6, pp_green_p6, pp_blue_p6, pp_red_p7, pp_green_p7, pp_blue_p7, pp_red_p8, pp_green_p8, pp_blue_p8, pp_red_p9, pp_green_p9, pp_blue_p9, pp_red_p10, pp_green_p10, pp_blue_p10,
|
| 445 |
+
red_curves, red_red_p0, red_green_p0, red_blue_p0, red_red_p1, red_green_p1, red_blue_p1, red_red_p2, red_green_p2, red_blue_p2, red_red_p3, red_green_p3, red_blue_p3, red_red_p4, red_green_p4, red_blue_p4, red_red_p5, red_green_p5, red_blue_p5, red_red_p6, red_green_p6, red_blue_p6, red_red_p7, red_green_p7, red_blue_p7, red_red_p8, red_green_p8, red_blue_p8, red_red_p9, red_green_p9, red_blue_p9, red_red_p10, red_green_p10, red_blue_p10,
|
| 446 |
+
green_curves, green_red_p0, green_green_p0, green_blue_p0, green_red_p1, green_green_p1, green_blue_p1, green_red_p2, green_green_p2, green_blue_p2, green_red_p3, green_green_p3, green_blue_p3, green_red_p4, green_green_p4, green_blue_p4, green_red_p5, green_green_p5, green_blue_p5, green_red_p6, green_green_p6, green_blue_p6, green_red_p7, green_green_p7, green_blue_p7, green_red_p8, green_green_p8, green_blue_p8, green_red_p9, green_green_p9, green_blue_p9, green_red_p10, green_green_p10, green_blue_p10,
|
| 447 |
+
blue_curves, blue_red_p0, blue_green_p0, blue_blue_p0, blue_red_p1, blue_green_p1, blue_blue_p1, blue_red_p2, blue_green_p2, blue_blue_p2, blue_red_p3, blue_green_p3, blue_blue_p3, blue_red_p4, blue_green_p4, blue_blue_p4, blue_red_p5, blue_green_p5, blue_blue_p5, blue_red_p6, blue_green_p6, blue_blue_p6, blue_red_p7, blue_green_p7, blue_blue_p7, blue_red_p8, blue_green_p8, blue_blue_p8, blue_red_p9, blue_green_p9, blue_blue_p9, blue_red_p10, blue_green_p10, blue_blue_p10,
|
| 448 |
+
out_image],
|
| 449 |
+
)
|
| 450 |
+
|
| 451 |
+
recompute_btn.click(
|
| 452 |
+
process_img_with_sliders,
|
| 453 |
+
inputs=[image,
|
| 454 |
+
oby_red_p0, oby_green_p0, oby_blue_p0, oby_red_p1, oby_green_p1, oby_blue_p1, oby_red_p2, oby_green_p2, oby_blue_p2, oby_red_p3, oby_green_p3, oby_blue_p3, oby_red_p4, oby_green_p4, oby_blue_p4, oby_red_p5, oby_green_p5, oby_blue_p5, oby_red_p6, oby_green_p6, oby_blue_p6, oby_red_p7, oby_green_p7, oby_blue_p7, oby_red_p8, oby_green_p8, oby_blue_p8, oby_red_p9, oby_green_p9, oby_blue_p9, oby_red_p10, oby_green_p10, oby_blue_p10,
|
| 455 |
+
achro_red_p0, achro_green_p0, achro_blue_p0, achro_red_p1, achro_green_p1, achro_blue_p1, achro_red_p2, achro_green_p2, achro_blue_p2, achro_red_p3, achro_green_p3, achro_blue_p3, achro_red_p4, achro_green_p4, achro_blue_p4, achro_red_p5, achro_green_p5, achro_blue_p5, achro_red_p6, achro_green_p6, achro_blue_p6, achro_red_p7, achro_green_p7, achro_blue_p7, achro_red_p8, achro_green_p8, achro_blue_p8, achro_red_p9, achro_green_p9, achro_blue_p9, achro_red_p10, achro_green_p10, achro_blue_p10,
|
| 456 |
+
pp_red_p0, pp_green_p0, pp_blue_p0, pp_red_p1, pp_green_p1, pp_blue_p1, pp_red_p2, pp_green_p2, pp_blue_p2, pp_red_p3, pp_green_p3, pp_blue_p3, pp_red_p4, pp_green_p4, pp_blue_p4, pp_red_p5, pp_green_p5, pp_blue_p5, pp_red_p6, pp_green_p6, pp_blue_p6, pp_red_p7, pp_green_p7, pp_blue_p7, pp_red_p8, pp_green_p8, pp_blue_p8, pp_red_p9, pp_green_p9, pp_blue_p9, pp_red_p10, pp_green_p10, pp_blue_p10,
|
| 457 |
+
red_red_p0, red_green_p0, red_blue_p0, red_red_p1, red_green_p1, red_blue_p1, red_red_p2, red_green_p2, red_blue_p2, red_red_p3, red_green_p3, red_blue_p3, red_red_p4, red_green_p4, red_blue_p4, red_red_p5, red_green_p5, red_blue_p5, red_red_p6, red_green_p6, red_blue_p6, red_red_p7, red_green_p7, red_blue_p7, red_red_p8, red_green_p8, red_blue_p8, red_red_p9, red_green_p9, red_blue_p9, red_red_p10, red_green_p10, red_blue_p10,
|
| 458 |
+
green_red_p0, green_green_p0, green_blue_p0, green_red_p1, green_green_p1, green_blue_p1, green_red_p2, green_green_p2, green_blue_p2, green_red_p3, green_green_p3, green_blue_p3, green_red_p4, green_green_p4, green_blue_p4, green_red_p5, green_green_p5, green_blue_p5, green_red_p6, green_green_p6, green_blue_p6, green_red_p7, green_green_p7, green_blue_p7, green_red_p8, green_green_p8, green_blue_p8, green_red_p9, green_green_p9, green_blue_p9, green_red_p10, green_green_p10, green_blue_p10,
|
| 459 |
+
blue_red_p0, blue_green_p0, blue_blue_p0, blue_red_p1, blue_green_p1, blue_blue_p1, blue_red_p2, blue_green_p2, blue_blue_p2, blue_red_p3, blue_green_p3, blue_blue_p3, blue_red_p4, blue_green_p4, blue_blue_p4, blue_red_p5, blue_green_p5, blue_blue_p5, blue_red_p6, blue_green_p6, blue_blue_p6, blue_red_p7, blue_green_p7, blue_blue_p7, blue_red_p8, blue_green_p8, blue_blue_p8, blue_red_p9, blue_green_p9, blue_blue_p9, blue_red_p10, blue_green_p10, blue_blue_p10],
|
| 460 |
+
outputs=[oby_curves, oby_red_p0, oby_green_p0, oby_blue_p0, oby_red_p1, oby_green_p1, oby_blue_p1, oby_red_p2, oby_green_p2, oby_blue_p2, oby_red_p3, oby_green_p3, oby_blue_p3, oby_red_p4, oby_green_p4, oby_blue_p4, oby_red_p5, oby_green_p5, oby_blue_p5, oby_red_p6, oby_green_p6, oby_blue_p6, oby_red_p7, oby_green_p7, oby_blue_p7, oby_red_p8, oby_green_p8, oby_blue_p8, oby_red_p9, oby_green_p9, oby_blue_p9, oby_red_p10, oby_green_p10, oby_blue_p10,
|
| 461 |
+
achro_curves, achro_red_p0, achro_green_p0, achro_blue_p0, achro_red_p1, achro_green_p1, achro_blue_p1, achro_red_p2, achro_green_p2, achro_blue_p2, achro_red_p3, achro_green_p3, achro_blue_p3, achro_red_p4, achro_green_p4, achro_blue_p4, achro_red_p5, achro_green_p5, achro_blue_p5, achro_red_p6, achro_green_p6, achro_blue_p6, achro_red_p7, achro_green_p7, achro_blue_p7, achro_red_p8, achro_green_p8, achro_blue_p8, achro_red_p9, achro_green_p9, achro_blue_p9, achro_red_p10, achro_green_p10, achro_blue_p10,
|
| 462 |
+
pink_purple_curves, pp_red_p0, pp_green_p0, pp_blue_p0, pp_red_p1, pp_green_p1, pp_blue_p1, pp_red_p2, pp_green_p2, pp_blue_p2, pp_red_p3, pp_green_p3, pp_blue_p3, pp_red_p4, pp_green_p4, pp_blue_p4, pp_red_p5, pp_green_p5, pp_blue_p5, pp_red_p6, pp_green_p6, pp_blue_p6, pp_red_p7, pp_green_p7, pp_blue_p7, pp_red_p8, pp_green_p8, pp_blue_p8, pp_red_p9, pp_green_p9, pp_blue_p9, pp_red_p10, pp_green_p10, pp_blue_p10,
|
| 463 |
+
red_curves, red_red_p0, red_green_p0, red_blue_p0, red_red_p1, red_green_p1, red_blue_p1, red_red_p2, red_green_p2, red_blue_p2, red_red_p3, red_green_p3, red_blue_p3, red_red_p4, red_green_p4, red_blue_p4, red_red_p5, red_green_p5, red_blue_p5, red_red_p6, red_green_p6, red_blue_p6, red_red_p7, red_green_p7, red_blue_p7, red_red_p8, red_green_p8, red_blue_p8, red_red_p9, red_green_p9, red_blue_p9, red_red_p10, red_green_p10, red_blue_p10,
|
| 464 |
+
green_curves, green_red_p0, green_green_p0, green_blue_p0, green_red_p1, green_green_p1, green_blue_p1, green_red_p2, green_green_p2, green_blue_p2, green_red_p3, green_green_p3, green_blue_p3, green_red_p4, green_green_p4, green_blue_p4, green_red_p5, green_green_p5, green_blue_p5, green_red_p6, green_green_p6, green_blue_p6, green_red_p7, green_green_p7, green_blue_p7, green_red_p8, green_green_p8, green_blue_p8, green_red_p9, green_green_p9, green_blue_p9, green_red_p10, green_green_p10, green_blue_p10,
|
| 465 |
+
blue_curves, blue_red_p0, blue_green_p0, blue_blue_p0, blue_red_p1, blue_green_p1, blue_blue_p1, blue_red_p2, blue_green_p2, blue_blue_p2, blue_red_p3, blue_green_p3, blue_blue_p3, blue_red_p4, blue_green_p4, blue_blue_p4, blue_red_p5, blue_green_p5, blue_blue_p5, blue_red_p6, blue_green_p6, blue_blue_p6, blue_red_p7, blue_green_p7, blue_blue_p7, blue_red_p8, blue_green_p8, blue_blue_p8, blue_red_p9, blue_green_p9, blue_blue_p9, blue_red_p10, blue_green_p10, blue_blue_p10,
|
| 466 |
+
out_image],
|
| 467 |
+
)
|
| 468 |
+
|
| 469 |
+
if __name__ == "__main__":
|
| 470 |
+
demo.launch()
|
assets/a4957-expertc.png
ADDED

|
assets/a4957-input.png
ADDED

|
assets/a4982-input.png
ADDED

|
assets/a4984-input.png
ADDED

|
assets/a4985-input.png
ADDED

|
assets/a4986-input.png
ADDED

|
assets/a4988-input.png
ADDED

|
assets/a4990-input.png
ADDED

|
assets/a4993-input.png
ADDED

|
assets/a4994-input.png
ADDED

|
assets/a4996-input.png
ADDED

|
assets/a4998-input.png
ADDED

|
assets/a5000-input.png
ADDED

|
assets/architecture-overview.png
ADDED
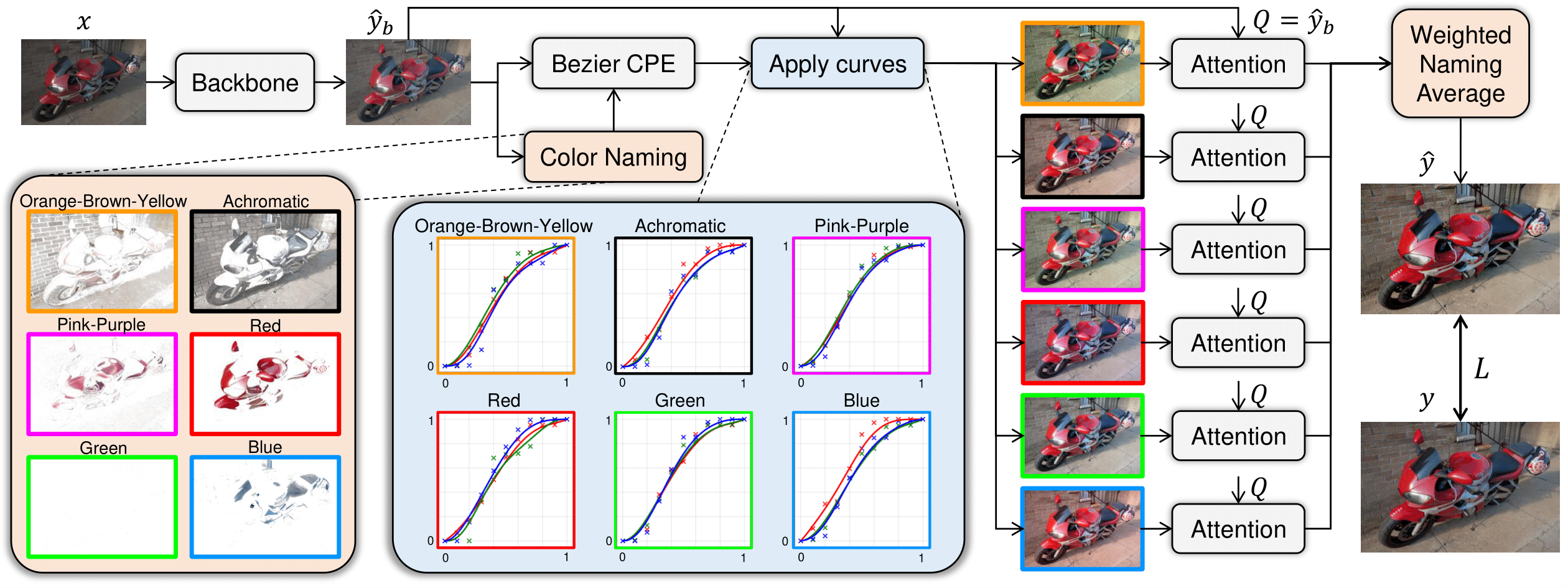
|
assets/thumbnail.png
ADDED

|
configs/mit5k_dpe_config.yaml
ADDED
|
@@ -0,0 +1,96 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
model:
|
| 2 |
+
ckpt_path: ~
|
| 3 |
+
backbone:
|
| 4 |
+
params:
|
| 5 |
+
input_channels: 3
|
| 6 |
+
output_channels: 3
|
| 7 |
+
encoder_dims: [4, 8, 16]
|
| 8 |
+
decoder_dims: [8, 4]
|
| 9 |
+
color_naming:
|
| 10 |
+
num_categories: 6
|
| 11 |
+
bezier_control_points_estimator:
|
| 12 |
+
params:
|
| 13 |
+
num_categories: ${model.color_naming.num_categories}
|
| 14 |
+
num_control_points: 10
|
| 15 |
+
local_fusion:
|
| 16 |
+
params:
|
| 17 |
+
att_in_dim: 3
|
| 18 |
+
num_categories: ${model.color_naming.num_categories}
|
| 19 |
+
max_pool_ksize1: 4
|
| 20 |
+
max_pool_ksize2: 2
|
| 21 |
+
encoder_dims: [8, 16]
|
| 22 |
+
|
| 23 |
+
data:
|
| 24 |
+
train:
|
| 25 |
+
target: mit5k
|
| 26 |
+
params:
|
| 27 |
+
input_path: /home/dserrano/Documents/datasets/FiveK-UEGAN/input
|
| 28 |
+
target_path: /home/dserrano/Documents/datasets/FiveK-UEGAN/expertC_gt
|
| 29 |
+
img_ids_filepath: mit5k_ids_filepath/dpe/images_train.txt
|
| 30 |
+
transform:
|
| 31 |
+
- type: RandomCrop
|
| 32 |
+
params:
|
| 33 |
+
size: [ 256, 256 ]
|
| 34 |
+
- type: Resize
|
| 35 |
+
params:
|
| 36 |
+
size: 256
|
| 37 |
+
- type: RandomHorizontalFlip
|
| 38 |
+
params:
|
| 39 |
+
p: 0.5
|
| 40 |
+
- type: RandomVerticalFlip
|
| 41 |
+
params:
|
| 42 |
+
p: 0.5
|
| 43 |
+
valid:
|
| 44 |
+
target: mit5k
|
| 45 |
+
params:
|
| 46 |
+
input_path: /home/dserrano/Documents/datasets/FiveK-UEGAN/input
|
| 47 |
+
target_path: /home/dserrano/Documents/datasets/FiveK-UEGAN/expertC_gt
|
| 48 |
+
img_ids_filepath: mit5k_ids_filepath/dpe/images_test.txt
|
| 49 |
+
|
| 50 |
+
test:
|
| 51 |
+
target: mit5k
|
| 52 |
+
params:
|
| 53 |
+
input_path: /home/dserrano/Documents/datasets/FiveK-UEGAN/input
|
| 54 |
+
target_path: /home/dserrano/Documents/datasets/FiveK-UEGAN/expertC_gt
|
| 55 |
+
img_ids_filepath: mit5k_ids_filepath/dpe/images_test.txt
|
| 56 |
+
|
| 57 |
+
train:
|
| 58 |
+
cuda_visible_device: 0
|
| 59 |
+
batch_size: 8
|
| 60 |
+
epochs: 100
|
| 61 |
+
valid_every: 1
|
| 62 |
+
optimizer:
|
| 63 |
+
type: Adam
|
| 64 |
+
params:
|
| 65 |
+
lr: 1e-4
|
| 66 |
+
betas: [ 0.9, 0.999 ]
|
| 67 |
+
eps: 1e-8
|
| 68 |
+
criterion:
|
| 69 |
+
type: backbone-L2-SSIM
|
| 70 |
+
params:
|
| 71 |
+
alpha: 0.5
|
| 72 |
+
ssim_window_size: 5
|
| 73 |
+
eval:
|
| 74 |
+
metrics:
|
| 75 |
+
- type: PSNR
|
| 76 |
+
params:
|
| 77 |
+
data_range: 1.0
|
| 78 |
+
- type: SSIM
|
| 79 |
+
params:
|
| 80 |
+
kernel_size: 11
|
| 81 |
+
- type: LPIPS
|
| 82 |
+
params:
|
| 83 |
+
net: vgg
|
| 84 |
+
version: 0.1
|
| 85 |
+
- type: deltaE00
|
| 86 |
+
- type: deltaEab
|
| 87 |
+
metric_to_save: PSNR
|
| 88 |
+
|
| 89 |
+
|
| 90 |
+
|
| 91 |
+
|
| 92 |
+
|
| 93 |
+
|
| 94 |
+
|
| 95 |
+
|
| 96 |
+
|
configs/mit5k_upe_config.yaml
ADDED
|
@@ -0,0 +1,90 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
model:
|
| 2 |
+
ckpt_path: ~
|
| 3 |
+
backbone:
|
| 4 |
+
params:
|
| 5 |
+
input_channels: 3
|
| 6 |
+
output_channels: 3
|
| 7 |
+
encoder_dims: [4, 8, 16]
|
| 8 |
+
decoder_dims: [8, 4]
|
| 9 |
+
color_naming:
|
| 10 |
+
num_categories: 6
|
| 11 |
+
bezier_control_points_estimator:
|
| 12 |
+
params:
|
| 13 |
+
num_categories: ${model.color_naming.num_categories}
|
| 14 |
+
num_control_points: 10
|
| 15 |
+
local_fusion:
|
| 16 |
+
params:
|
| 17 |
+
att_in_dim: 3
|
| 18 |
+
num_categories: ${model.color_naming.num_categories}
|
| 19 |
+
max_pool_ksize1: 4
|
| 20 |
+
max_pool_ksize2: 2
|
| 21 |
+
encoder_dims: [8, 16]
|
| 22 |
+
|
| 23 |
+
data:
|
| 24 |
+
train:
|
| 25 |
+
target: mit5k
|
| 26 |
+
params:
|
| 27 |
+
input_path: /home/dserrano/Documents/datasets/FiveK-UEGAN/input
|
| 28 |
+
target_path: /home/dserrano/Documents/datasets/FiveK-UEGAN/expertC_gt
|
| 29 |
+
img_ids_filepath: /home/dserrano/Workspace/DeepLPF/adobe5k_upe/images_train.txt
|
| 30 |
+
transform:
|
| 31 |
+
- type: RandomCrop
|
| 32 |
+
params:
|
| 33 |
+
size: [ 256, 256 ]
|
| 34 |
+
- type: Resize
|
| 35 |
+
params:
|
| 36 |
+
size: 256
|
| 37 |
+
- type: RandomHorizontalFlip
|
| 38 |
+
params:
|
| 39 |
+
p: 0.5
|
| 40 |
+
- type: RandomVerticalFlip
|
| 41 |
+
params:
|
| 42 |
+
p: 0.5
|
| 43 |
+
|
| 44 |
+
test:
|
| 45 |
+
target: mit5k
|
| 46 |
+
params:
|
| 47 |
+
input_path: /home/dserrano/Documents/datasets/FiveK-UEGAN/input
|
| 48 |
+
target_path: /home/dserrano/Documents/datasets/FiveK-UEGAN/expertC_gt
|
| 49 |
+
img_ids_filepath: /home/dserrano/Workspace/DeepLPF/adobe5k_upe/images_train.txt
|
| 50 |
+
|
| 51 |
+
train:
|
| 52 |
+
cuda_visible_device: 0
|
| 53 |
+
batch_size: 8
|
| 54 |
+
epochs: 100
|
| 55 |
+
valid_every: 1
|
| 56 |
+
optimizer:
|
| 57 |
+
type: Adam
|
| 58 |
+
params:
|
| 59 |
+
lr: 1e-4
|
| 60 |
+
betas: [ 0.9, 0.999 ]
|
| 61 |
+
eps: 1e-8
|
| 62 |
+
criterion:
|
| 63 |
+
type: backbone-L2-SSIM
|
| 64 |
+
params:
|
| 65 |
+
alpha: 0.5
|
| 66 |
+
ssim_window_size: 5
|
| 67 |
+
eval:
|
| 68 |
+
metrics:
|
| 69 |
+
- type: PSNR
|
| 70 |
+
params:
|
| 71 |
+
data_range: 1.0
|
| 72 |
+
- type: SSIM
|
| 73 |
+
params:
|
| 74 |
+
kernel_size: 11
|
| 75 |
+
- type: LPIPS
|
| 76 |
+
params:
|
| 77 |
+
net: vgg
|
| 78 |
+
version: 0.1
|
| 79 |
+
- type: deltaE00
|
| 80 |
+
- type: deltaEab
|
| 81 |
+
metric_to_save: PSNR
|
| 82 |
+
|
| 83 |
+
|
| 84 |
+
|
| 85 |
+
|
| 86 |
+
|
| 87 |
+
|
| 88 |
+
|
| 89 |
+
|
| 90 |
+
|
data/datasets.py
ADDED
|
@@ -0,0 +1,109 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
import os
|
| 2 |
+
import logging
|
| 3 |
+
import numpy as np
|
| 4 |
+
from glob import glob
|
| 5 |
+
from PIL import Image
|
| 6 |
+
from torch.utils.data import Dataset
|
| 7 |
+
from torchvision import transforms
|
| 8 |
+
from torchvision.transforms import functional as TF
|
| 9 |
+
from torchvision.transforms.functional import to_tensor
|
| 10 |
+
from data.image_transformations import get_transforms
|
| 11 |
+
|
| 12 |
+
class MIT5KDataset(Dataset):
|
| 13 |
+
def __init__(self, input_path, target_path, img_ids_filepath, transform=None):
|
| 14 |
+
self.input_path = input_path
|
| 15 |
+
self.target_path = target_path
|
| 16 |
+
self.transform = transform
|
| 17 |
+
self.img_ids = self._read_img_ids(img_ids_filepath)
|
| 18 |
+
self.data = self._create_data_list()
|
| 19 |
+
if transform is not None:
|
| 20 |
+
self.image_transforms = get_transforms(transform)
|
| 21 |
+
else:
|
| 22 |
+
self.image_transforms = None
|
| 23 |
+
|
| 24 |
+
def _read_img_ids(self, img_ids_filepath):
|
| 25 |
+
# Read the image IDs from the txt file
|
| 26 |
+
with open(img_ids_filepath, 'r') as f:
|
| 27 |
+
img_ids = [line.strip() for line in f.readlines()]
|
| 28 |
+
return img_ids
|
| 29 |
+
|
| 30 |
+
def _create_data_list(self):
|
| 31 |
+
# Create a list of dictionaries with 'input_path', 'target_path' and 'name'
|
| 32 |
+
data_list = []
|
| 33 |
+
for input_file in glob(os.path.join(self.input_path, "*")):
|
| 34 |
+
img_id = os.path.basename(input_file).split('-')[0]
|
| 35 |
+
if img_id in self.img_ids:
|
| 36 |
+
target_file = os.path.join(self.target_path, os.path.basename(os.path.basename(input_file)))
|
| 37 |
+
if not os.path.exists(target_file):
|
| 38 |
+
raise FileNotFoundError(f"Target file {target_file} not found. While input file {input_file} was found.")
|
| 39 |
+
data_list.append({'input_path': input_file, 'target_path': target_file, 'name': img_id})
|
| 40 |
+
|
| 41 |
+
return data_list
|
| 42 |
+
|
| 43 |
+
def __len__(self):
|
| 44 |
+
return len(self.data)
|
| 45 |
+
|
| 46 |
+
def __getitem__(self, idx):
|
| 47 |
+
data = self.data[idx]
|
| 48 |
+
input_image, target_image = self._load_image_pair(data['input_path'], data['target_path'])
|
| 49 |
+
|
| 50 |
+
return {'input_image': input_image, 'target_image': target_image, 'name':data['name']}
|
| 51 |
+
|
| 52 |
+
def _load_image_pair(self, img1_path, img2_path):
|
| 53 |
+
img1_tensor = to_tensor(np.array(Image.open(img1_path).convert('RGB')))
|
| 54 |
+
img2_tensor = to_tensor(np.array(Image.open(img2_path).convert('RGB')))
|
| 55 |
+
|
| 56 |
+
if self.image_transforms is not None:
|
| 57 |
+
for image_transform in self.image_transforms:
|
| 58 |
+
img1_tensor, img2_tensor = image_transform(img1_tensor, img2_tensor)
|
| 59 |
+
|
| 60 |
+
return img1_tensor, img2_tensor
|
| 61 |
+
|
| 62 |
+
#class PPR10KDataset(Dataset):
|
| 63 |
+
|
| 64 |
+
|
| 65 |
+
def get_single_dataset(type, params):
|
| 66 |
+
if type == 'mit5k':
|
| 67 |
+
return MIT5KDataset(**params)
|
| 68 |
+
elif type == 'ppr10k':
|
| 69 |
+
# TODO:
|
| 70 |
+
return PPR10KDataset(**params)
|
| 71 |
+
else:
|
| 72 |
+
raise ValueError(f"Unsupported dataset type: {type}")
|
| 73 |
+
|
| 74 |
+
|
| 75 |
+
def get_datasets(config):
|
| 76 |
+
"""Returns the datsaets based on the configuration file."""
|
| 77 |
+
|
| 78 |
+
if len(config) == 2:
|
| 79 |
+
train_dataset = get_single_dataset(config.train.target, config.train.params)
|
| 80 |
+
test_dataset = get_single_dataset(config.test.target, config.test.params)
|
| 81 |
+
return train_dataset, None, test_dataset
|
| 82 |
+
|
| 83 |
+
elif len(config) == 3:
|
| 84 |
+
train_dataset = get_single_dataset(config.train.target, config.train.params)
|
| 85 |
+
val_dataset = get_single_dataset(config.valid.target, config.valid.params)
|
| 86 |
+
test_dataset = get_single_dataset(config.test.target, config.test.params)
|
| 87 |
+
return train_dataset, val_dataset, test_dataset
|
| 88 |
+
|
| 89 |
+
else:
|
| 90 |
+
raise ValueError("The number of datasets should be 2 (train/test) or 3 (train/valid/test).")
|
| 91 |
+
|
| 92 |
+
if __name__ == "__main__":
|
| 93 |
+
from omegaconf import OmegaConf
|
| 94 |
+
config = OmegaConf.load("../configs/mit5k_upe_config.yaml")
|
| 95 |
+
|
| 96 |
+
dataset = MIT5KDataset(**config.data.train.params)
|
| 97 |
+
input_img, target_img, name = dataset[0]
|
| 98 |
+
|
| 99 |
+
import matplotlib.pyplot as plt
|
| 100 |
+
plt.subplot(1, 2, 1)
|
| 101 |
+
plt.imshow(input_img.squeeze().permute(1, 2, 0).numpy())
|
| 102 |
+
plt.title("Input Image")
|
| 103 |
+
plt.subplot(1, 2, 2)
|
| 104 |
+
plt.imshow(target_img.squeeze().permute(1, 2, 0).numpy())
|
| 105 |
+
plt.title("Target Image")
|
| 106 |
+
plt.show()
|
| 107 |
+
|
| 108 |
+
|
| 109 |
+
|
data/image_transformations.py
ADDED
|
@@ -0,0 +1,61 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
import random
|
| 2 |
+
import torchvision.transforms.functional as F
|
| 3 |
+
from torchvision import transforms
|
| 4 |
+
|
| 5 |
+
class RandomCropPair:
|
| 6 |
+
def __init__(self, size):
|
| 7 |
+
self.size = size
|
| 8 |
+
|
| 9 |
+
def __call__(self, img1, img2):
|
| 10 |
+
i, j, h, w = transforms.RandomCrop.get_params(img1, self.size)
|
| 11 |
+
img1 = F.crop(img1, i, j, h, w)
|
| 12 |
+
img2 = F.crop(img2, i, j, h, w)
|
| 13 |
+
return img1, img2
|
| 14 |
+
|
| 15 |
+
class ResizePair:
|
| 16 |
+
def __init__(self, size):
|
| 17 |
+
self.size = size
|
| 18 |
+
|
| 19 |
+
def __call__(self, img1, img2):
|
| 20 |
+
# antialias=True is used to avoid torchvision warning
|
| 21 |
+
img1 = F.resize(img1, self.size, antialias=True)
|
| 22 |
+
img2 = F.resize(img2, self.size, antialias=True)
|
| 23 |
+
return img1, img2
|
| 24 |
+
|
| 25 |
+
class RandomHorizontalFlipPair:
|
| 26 |
+
def __init__(self, p=0.5):
|
| 27 |
+
self.p = p
|
| 28 |
+
|
| 29 |
+
def __call__(self, img1, img2):
|
| 30 |
+
if random.random() < self.p:
|
| 31 |
+
img1 = F.hflip(img1)
|
| 32 |
+
img2 = F.hflip(img2)
|
| 33 |
+
return img1, img2
|
| 34 |
+
|
| 35 |
+
class RandomVerticalFlipPair:
|
| 36 |
+
def __init__(self, p=0.5):
|
| 37 |
+
self.p = p
|
| 38 |
+
|
| 39 |
+
def __call__(self, img1, img2):
|
| 40 |
+
if random.random() < self.p:
|
| 41 |
+
img1 = F.vflip(img1)
|
| 42 |
+
img2 = F.vflip(img2)
|
| 43 |
+
return img1, img2
|
| 44 |
+
|
| 45 |
+
def get_transforms(transforms_config):
|
| 46 |
+
transform_list = []
|
| 47 |
+
for transform in transforms_config:
|
| 48 |
+
transform_type = transform['type']
|
| 49 |
+
params = transform['params']
|
| 50 |
+
if transform_type == 'RandomCrop':
|
| 51 |
+
transform_list.append(RandomCropPair(**params))
|
| 52 |
+
elif transform_type == 'Resize':
|
| 53 |
+
transform_list.append(ResizePair(**params))
|
| 54 |
+
elif transform_type == 'RandomHorizontalFlip':
|
| 55 |
+
transform_list.append(RandomHorizontalFlipPair(**params))
|
| 56 |
+
elif transform_type == 'RandomVerticalFlip':
|
| 57 |
+
transform_list.append(RandomVerticalFlipPair(**params))
|
| 58 |
+
else:
|
| 59 |
+
raise ValueError(f"Unsupported transform type: {transform_type}")
|
| 60 |
+
|
| 61 |
+
return transform_list
|
mit5k_ids_filepath/dpe/images_test.txt
ADDED
|
@@ -0,0 +1,50 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
a4501
|
| 2 |
+
a4502
|
| 3 |
+
a4503
|
| 4 |
+
a4504
|
| 5 |
+
a4505
|
| 6 |
+
a4506
|
| 7 |
+
a4507
|
| 8 |
+
a4508
|
| 9 |
+
a4509
|
| 10 |
+
a4510
|
| 11 |
+
a4511
|
| 12 |
+
a4512
|
| 13 |
+
a4513
|
| 14 |
+
a4514
|
| 15 |
+
a4515
|
| 16 |
+
a4516
|
| 17 |
+
a4517
|
| 18 |
+
a4518
|
| 19 |
+
a4519
|
| 20 |
+
a4520
|
| 21 |
+
a4521
|
| 22 |
+
a4522
|
| 23 |
+
a4523
|
| 24 |
+
a4524
|
| 25 |
+
a4525
|
| 26 |
+
a4526
|
| 27 |
+
a4527
|
| 28 |
+
a4528
|
| 29 |
+
a4529
|
| 30 |
+
a4530
|
| 31 |
+
a4531
|
| 32 |
+
a4532
|
| 33 |
+
a4533
|
| 34 |
+
a4534
|
| 35 |
+
a4535
|
| 36 |
+
a4536
|
| 37 |
+
a4537
|
| 38 |
+
a4538
|
| 39 |
+
a4539
|
| 40 |
+
a4540
|
| 41 |
+
a4541
|
| 42 |
+
a4542
|
| 43 |
+
a4543
|
| 44 |
+
a4544
|
| 45 |
+
a4545
|
| 46 |
+
a4546
|
| 47 |
+
a4547
|
| 48 |
+
a4548
|
| 49 |
+
a4549
|
| 50 |
+
a4550
|
mit5k_ids_filepath/dpe/images_train.txt
ADDED
|
@@ -0,0 +1,62 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
a0001
|
| 2 |
+
a0002
|
| 3 |
+
a0003
|
| 4 |
+
a0004
|
| 5 |
+
a0005
|
| 6 |
+
a0006
|
| 7 |
+
a0007
|
| 8 |
+
a0008
|
| 9 |
+
a0009
|
| 10 |
+
a0010
|
| 11 |
+
a0011
|
| 12 |
+
a0012
|
| 13 |
+
a0013
|
| 14 |
+
a0014
|
| 15 |
+
a0015
|
| 16 |
+
a0016
|
| 17 |
+
a0017
|
| 18 |
+
a0018
|
| 19 |
+
a0019
|
| 20 |
+
a0020
|
| 21 |
+
a0021
|
| 22 |
+
a0022
|
| 23 |
+
a0023
|
| 24 |
+
a0024
|
| 25 |
+
a0025
|
| 26 |
+
a0026
|
| 27 |
+
a0027
|
| 28 |
+
a0028
|
| 29 |
+
a0029
|
| 30 |
+
a0030
|
| 31 |
+
a0031
|
| 32 |
+
a0032
|
| 33 |
+
a0033
|
| 34 |
+
a0034
|
| 35 |
+
a0035
|
| 36 |
+
a0036
|
| 37 |
+
a0037
|
| 38 |
+
a0038
|
| 39 |
+
a0039
|
| 40 |
+
a0040
|
| 41 |
+
a0041
|
| 42 |
+
a0042
|
| 43 |
+
a0043
|
| 44 |
+
a0044
|
| 45 |
+
a0045
|
| 46 |
+
a0046
|
| 47 |
+
a0047
|
| 48 |
+
a0048
|
| 49 |
+
a0049
|
| 50 |
+
a0050
|
| 51 |
+
a0051
|
| 52 |
+
a0052
|
| 53 |
+
a0053
|
| 54 |
+
a0054
|
| 55 |
+
a0055
|
| 56 |
+
a0056
|
| 57 |
+
a0057
|
| 58 |
+
a0058
|
| 59 |
+
a0059
|
| 60 |
+
a0060
|
| 61 |
+
a0061
|
| 62 |
+
a0062
|
mit5k_ids_filepath/dpe/images_valid.txt
ADDED
|
@@ -0,0 +1,2250 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
a2251
|
| 2 |
+
a2252
|
| 3 |
+
a2253
|
| 4 |
+
a2254
|
| 5 |
+
a2255
|
| 6 |
+
a2256
|
| 7 |
+
a2257
|
| 8 |
+
a2258
|
| 9 |
+
a2259
|
| 10 |
+
a2260
|
| 11 |
+
a2261
|
| 12 |
+
a2262
|
| 13 |
+
a2263
|
| 14 |
+
a2264
|
| 15 |
+
a2265
|
| 16 |
+
a2266
|
| 17 |
+
a2267
|
| 18 |
+
a2268
|
| 19 |
+
a2269
|
| 20 |
+
a2270
|
| 21 |
+
a2271
|
| 22 |
+
a2272
|
| 23 |
+
a2273
|
| 24 |
+
a2274
|
| 25 |
+
a2275
|
| 26 |
+
a2276
|
| 27 |
+
a2277
|
| 28 |
+
a2278
|
| 29 |
+
a2279
|
| 30 |
+
a2280
|
| 31 |
+
a2281
|
| 32 |
+
a2282
|
| 33 |
+
a2283
|
| 34 |
+
a2284
|
| 35 |
+
a2285
|
| 36 |
+
a2286
|
| 37 |
+
a2287
|
| 38 |
+
a2288
|
| 39 |
+
a2289
|
| 40 |
+
a2290
|
| 41 |
+
a2291
|
| 42 |
+
a2292
|
| 43 |
+
a2293
|
| 44 |
+
a2294
|
| 45 |
+
a2295
|
| 46 |
+
a2296
|
| 47 |
+
a2297
|
| 48 |
+
a2298
|
| 49 |
+
a2299
|
| 50 |
+
a2300
|
| 51 |
+
a2301
|
| 52 |
+
a2302
|
| 53 |
+
a2303
|
| 54 |
+
a2304
|
| 55 |
+
a2305
|
| 56 |
+
a2306
|
| 57 |
+
a2307
|
| 58 |
+
a2308
|
| 59 |
+
a2309
|
| 60 |
+
a2310
|
| 61 |
+
a2311
|
| 62 |
+
a2312
|
| 63 |
+
a2313
|
| 64 |
+
a2314
|
| 65 |
+
a2315
|
| 66 |
+
a2316
|
| 67 |
+
a2317
|
| 68 |
+
a2318
|
| 69 |
+
a2319
|
| 70 |
+
a2320
|
| 71 |
+
a2321
|
| 72 |
+
a2322
|
| 73 |
+
a2323
|
| 74 |
+
a2324
|
| 75 |
+
a2325
|
| 76 |
+
a2326
|
| 77 |
+
a2327
|
| 78 |
+
a2328
|
| 79 |
+
a2329
|
| 80 |
+
a2330
|
| 81 |
+
a2331
|
| 82 |
+
a2332
|
| 83 |
+
a2333
|
| 84 |
+
a2334
|
| 85 |
+
a2335
|
| 86 |
+
a2336
|
| 87 |
+
a2337
|
| 88 |
+
a2338
|
| 89 |
+
a2339
|
| 90 |
+
a2340
|
| 91 |
+
a2341
|
| 92 |
+
a2342
|
| 93 |
+
a2343
|
| 94 |
+
a2344
|
| 95 |
+
a2345
|
| 96 |
+
a2346
|
| 97 |
+
a2347
|
| 98 |
+
a2348
|
| 99 |
+
a2349
|
| 100 |
+
a2350
|
| 101 |
+
a2351
|
| 102 |
+
a2352
|
| 103 |
+
a2353
|
| 104 |
+
a2354
|
| 105 |
+
a2355
|
| 106 |
+
a2356
|
| 107 |
+
a2357
|
| 108 |
+
a2358
|
| 109 |
+
a2359
|
| 110 |
+
a2360
|
| 111 |
+
a2361
|
| 112 |
+
a2362
|
| 113 |
+
a2363
|
| 114 |
+
a2364
|
| 115 |
+
a2365
|
| 116 |
+
a2366
|
| 117 |
+
a2367
|
| 118 |
+
a2368
|
| 119 |
+
a2369
|
| 120 |
+
a2370
|
| 121 |
+
a2371
|
| 122 |
+
a2372
|
| 123 |
+
a2373
|
| 124 |
+
a2374
|
| 125 |
+
a2375
|
| 126 |
+
a2376
|
| 127 |
+
a2377
|
| 128 |
+
a2378
|
| 129 |
+
a2379
|
| 130 |
+
a2380
|
| 131 |
+
a2381
|
| 132 |
+
a2382
|
| 133 |
+
a2383
|
| 134 |
+
a2384
|
| 135 |
+
a2385
|
| 136 |
+
a2386
|
| 137 |
+
a2387
|
| 138 |
+
a2388
|
| 139 |
+
a2389
|
| 140 |
+
a2390
|
| 141 |
+
a2391
|
| 142 |
+
a2392
|
| 143 |
+
a2393
|
| 144 |
+
a2394
|
| 145 |
+
a2395
|
| 146 |
+
a2396
|
| 147 |
+
a2397
|
| 148 |
+
a2398
|
| 149 |
+
a2399
|
| 150 |
+
a2400
|
| 151 |
+
a2401
|
| 152 |
+
a2402
|
| 153 |
+
a2403
|
| 154 |
+
a2404
|
| 155 |
+
a2405
|
| 156 |
+
a2406
|
| 157 |
+
a2407
|
| 158 |
+
a2408
|
| 159 |
+
a2409
|
| 160 |
+
a2410
|
| 161 |
+
a2411
|
| 162 |
+
a2412
|
| 163 |
+
a2413
|
| 164 |
+
a2414
|
| 165 |
+
a2415
|
| 166 |
+
a2416
|
| 167 |
+
a2417
|
| 168 |
+
a2418
|
| 169 |
+
a2419
|
| 170 |
+
a2420
|
| 171 |
+
a2421
|
| 172 |
+
a2422
|
| 173 |
+
a2423
|
| 174 |
+
a2424
|
| 175 |
+
a2425
|
| 176 |
+
a2426
|
| 177 |
+
a2427
|
| 178 |
+
a2428
|
| 179 |
+
a2429
|
| 180 |
+
a2430
|
| 181 |
+
a2431
|
| 182 |
+
a2432
|
| 183 |
+
a2433
|
| 184 |
+
a2434
|
| 185 |
+
a2435
|
| 186 |
+
a2436
|
| 187 |
+
a2437
|
| 188 |
+
a2438
|
| 189 |
+
a2439
|
| 190 |
+
a2440
|
| 191 |
+
a2441
|
| 192 |
+
a2442
|
| 193 |
+
a2443
|
| 194 |
+
a2444
|
| 195 |
+
a2445
|
| 196 |
+
a2446
|
| 197 |
+
a2447
|
| 198 |
+
a2448
|
| 199 |
+
a2449
|
| 200 |
+
a2450
|
| 201 |
+
a2451
|
| 202 |
+
a2452
|
| 203 |
+
a2453
|
| 204 |
+
a2454
|
| 205 |
+
a2455
|
| 206 |
+
a2456
|
| 207 |
+
a2457
|
| 208 |
+
a2458
|
| 209 |
+
a2459
|
| 210 |
+
a2460
|
| 211 |
+
a2461
|
| 212 |
+
a2462
|
| 213 |
+
a2463
|
| 214 |
+
a2464
|
| 215 |
+
a2465
|
| 216 |
+
a2466
|
| 217 |
+
a2467
|
| 218 |
+
a2468
|
| 219 |
+
a2469
|
| 220 |
+
a2470
|
| 221 |
+
a2471
|
| 222 |
+
a2472
|
| 223 |
+
a2473
|
| 224 |
+
a2474
|
| 225 |
+
a2475
|
| 226 |
+
a2476
|
| 227 |
+
a2477
|
| 228 |
+
a2478
|
| 229 |
+
a2479
|
| 230 |
+
a2480
|
| 231 |
+
a2481
|
| 232 |
+
a2482
|
| 233 |
+
a2483
|
| 234 |
+
a2484
|
| 235 |
+
a2485
|
| 236 |
+
a2486
|
| 237 |
+
a2487
|
| 238 |
+
a2488
|
| 239 |
+
a2489
|
| 240 |
+
a2490
|
| 241 |
+
a2491
|
| 242 |
+
a2492
|
| 243 |
+
a2493
|
| 244 |
+
a2494
|
| 245 |
+
a2495
|
| 246 |
+
a2496
|
| 247 |
+
a2497
|
| 248 |
+
a2498
|
| 249 |
+
a2499
|
| 250 |
+
a2500
|
| 251 |
+
a2501
|
| 252 |
+
a2502
|
| 253 |
+
a2503
|
| 254 |
+
a2504
|
| 255 |
+
a2505
|
| 256 |
+
a2506
|
| 257 |
+
a2507
|
| 258 |
+
a2508
|
| 259 |
+
a2509
|
| 260 |
+
a2510
|
| 261 |
+
a2511
|
| 262 |
+
a2512
|
| 263 |
+
a2513
|
| 264 |
+
a2514
|
| 265 |
+
a2515
|
| 266 |
+
a2516
|
| 267 |
+
a2517
|
| 268 |
+
a2518
|
| 269 |
+
a2519
|
| 270 |
+
a2520
|
| 271 |
+
a2521
|
| 272 |
+
a2522
|
| 273 |
+
a2523
|
| 274 |
+
a2524
|
| 275 |
+
a2525
|
| 276 |
+
a2526
|
| 277 |
+
a2527
|
| 278 |
+
a2528
|
| 279 |
+
a2529
|
| 280 |
+
a2530
|
| 281 |
+
a2531
|
| 282 |
+
a2532
|
| 283 |
+
a2533
|
| 284 |
+
a2534
|
| 285 |
+
a2535
|
| 286 |
+
a2536
|
| 287 |
+
a2537
|
| 288 |
+
a2538
|
| 289 |
+
a2539
|
| 290 |
+
a2540
|
| 291 |
+
a2541
|
| 292 |
+
a2542
|
| 293 |
+
a2543
|
| 294 |
+
a2544
|
| 295 |
+
a2545
|
| 296 |
+
a2546
|
| 297 |
+
a2547
|
| 298 |
+
a2548
|
| 299 |
+
a2549
|
| 300 |
+
a2550
|
| 301 |
+
a2551
|
| 302 |
+
a2552
|
| 303 |
+
a2553
|
| 304 |
+
a2554
|
| 305 |
+
a2555
|
| 306 |
+
a2556
|
| 307 |
+
a2557
|
| 308 |
+
a2558
|
| 309 |
+
a2559
|
| 310 |
+
a2560
|
| 311 |
+
a2561
|
| 312 |
+
a2562
|
| 313 |
+
a2563
|
| 314 |
+
a2564
|
| 315 |
+
a2565
|
| 316 |
+
a2566
|
| 317 |
+
a2567
|
| 318 |
+
a2568
|
| 319 |
+
a2569
|
| 320 |
+
a2570
|
| 321 |
+
a2571
|
| 322 |
+
a2572
|
| 323 |
+
a2573
|
| 324 |
+
a2574
|
| 325 |
+
a2575
|
| 326 |
+
a2576
|
| 327 |
+
a2577
|
| 328 |
+
a2578
|
| 329 |
+
a2579
|
| 330 |
+
a2580
|
| 331 |
+
a2581
|
| 332 |
+
a2582
|
| 333 |
+
a2583
|
| 334 |
+
a2584
|
| 335 |
+
a2585
|
| 336 |
+
a2586
|
| 337 |
+
a2587
|
| 338 |
+
a2588
|
| 339 |
+
a2589
|
| 340 |
+
a2590
|
| 341 |
+
a2591
|
| 342 |
+
a2592
|
| 343 |
+
a2593
|
| 344 |
+
a2594
|
| 345 |
+
a2595
|
| 346 |
+
a2596
|
| 347 |
+
a2597
|
| 348 |
+
a2598
|
| 349 |
+
a2599
|
| 350 |
+
a2600
|
| 351 |
+
a2601
|
| 352 |
+
a2602
|
| 353 |
+
a2603
|
| 354 |
+
a2604
|
| 355 |
+
a2605
|
| 356 |
+
a2606
|
| 357 |
+
a2607
|
| 358 |
+
a2608
|
| 359 |
+
a2609
|
| 360 |
+
a2610
|
| 361 |
+
a2611
|
| 362 |
+
a2612
|
| 363 |
+
a2613
|
| 364 |
+
a2614
|
| 365 |
+
a2615
|
| 366 |
+
a2616
|
| 367 |
+
a2617
|
| 368 |
+
a2618
|
| 369 |
+
a2619
|
| 370 |
+
a2620
|
| 371 |
+
a2621
|
| 372 |
+
a2622
|
| 373 |
+
a2623
|
| 374 |
+
a2624
|
| 375 |
+
a2625
|
| 376 |
+
a2626
|
| 377 |
+
a2627
|
| 378 |
+
a2628
|
| 379 |
+
a2629
|
| 380 |
+
a2630
|
| 381 |
+
a2631
|
| 382 |
+
a2632
|
| 383 |
+
a2633
|
| 384 |
+
a2634
|
| 385 |
+
a2635
|
| 386 |
+
a2636
|
| 387 |
+
a2637
|
| 388 |
+
a2638
|
| 389 |
+
a2639
|
| 390 |
+
a2640
|
| 391 |
+
a2641
|
| 392 |
+
a2642
|
| 393 |
+
a2643
|
| 394 |
+
a2644
|
| 395 |
+
a2645
|
| 396 |
+
a2646
|
| 397 |
+
a2647
|
| 398 |
+
a2648
|
| 399 |
+
a2649
|
| 400 |
+
a2650
|
| 401 |
+
a2651
|
| 402 |
+
a2652
|
| 403 |
+
a2653
|
| 404 |
+
a2654
|
| 405 |
+
a2655
|
| 406 |
+
a2656
|
| 407 |
+
a2657
|
| 408 |
+
a2658
|
| 409 |
+
a2659
|
| 410 |
+
a2660
|
| 411 |
+
a2661
|
| 412 |
+
a2662
|
| 413 |
+
a2663
|
| 414 |
+
a2664
|
| 415 |
+
a2665
|
| 416 |
+
a2666
|
| 417 |
+
a2667
|
| 418 |
+
a2668
|
| 419 |
+
a2669
|
| 420 |
+
a2670
|
| 421 |
+
a2671
|
| 422 |
+
a2672
|
| 423 |
+
a2673
|
| 424 |
+
a2674
|
| 425 |
+
a2675
|
| 426 |
+
a2676
|
| 427 |
+
a2677
|
| 428 |
+
a2678
|
| 429 |
+
a2679
|
| 430 |
+
a2680
|
| 431 |
+
a2681
|
| 432 |
+
a2682
|
| 433 |
+
a2683
|
| 434 |
+
a2684
|
| 435 |
+
a2685
|
| 436 |
+
a2686
|
| 437 |
+
a2687
|
| 438 |
+
a2688
|
| 439 |
+
a2689
|
| 440 |
+
a2690
|
| 441 |
+
a2691
|
| 442 |
+
a2692
|
| 443 |
+
a2693
|
| 444 |
+
a2694
|
| 445 |
+
a2695
|
| 446 |
+
a2696
|
| 447 |
+
a2697
|
| 448 |
+
a2698
|
| 449 |
+
a2699
|
| 450 |
+
a2700
|
| 451 |
+
a2701
|
| 452 |
+
a2702
|
| 453 |
+
a2703
|
| 454 |
+
a2704
|
| 455 |
+
a2705
|
| 456 |
+
a2706
|
| 457 |
+
a2707
|
| 458 |
+
a2708
|
| 459 |
+
a2709
|
| 460 |
+
a2710
|
| 461 |
+
a2711
|
| 462 |
+
a2712
|
| 463 |
+
a2713
|
| 464 |
+
a2714
|
| 465 |
+
a2715
|
| 466 |
+
a2716
|
| 467 |
+
a2717
|
| 468 |
+
a2718
|
| 469 |
+
a2719
|
| 470 |
+
a2720
|
| 471 |
+
a2721
|
| 472 |
+
a2722
|
| 473 |
+
a2723
|
| 474 |
+
a2724
|
| 475 |
+
a2725
|
| 476 |
+
a2726
|
| 477 |
+
a2727
|
| 478 |
+
a2728
|
| 479 |
+
a2729
|
| 480 |
+
a2730
|
| 481 |
+
a2731
|
| 482 |
+
a2732
|
| 483 |
+
a2733
|
| 484 |
+
a2734
|
| 485 |
+
a2735
|
| 486 |
+
a2736
|
| 487 |
+
a2737
|
| 488 |
+
a2738
|
| 489 |
+
a2739
|
| 490 |
+
a2740
|
| 491 |
+
a2741
|
| 492 |
+
a2742
|
| 493 |
+
a2743
|
| 494 |
+
a2744
|
| 495 |
+
a2745
|
| 496 |
+
a2746
|
| 497 |
+
a2747
|
| 498 |
+
a2748
|
| 499 |
+
a2749
|
| 500 |
+
a2750
|
| 501 |
+
a2751
|
| 502 |
+
a2752
|
| 503 |
+
a2753
|
| 504 |
+
a2754
|
| 505 |
+
a2755
|
| 506 |
+
a2756
|
| 507 |
+
a2757
|
| 508 |
+
a2758
|
| 509 |
+
a2759
|
| 510 |
+
a2760
|
| 511 |
+
a2761
|
| 512 |
+
a2762
|
| 513 |
+
a2763
|
| 514 |
+
a2764
|
| 515 |
+
a2765
|
| 516 |
+
a2766
|
| 517 |
+
a2767
|
| 518 |
+
a2768
|
| 519 |
+
a2769
|
| 520 |
+
a2770
|
| 521 |
+
a2771
|
| 522 |
+
a2772
|
| 523 |
+
a2773
|
| 524 |
+
a2774
|
| 525 |
+
a2775
|
| 526 |
+
a2776
|
| 527 |
+
a2777
|
| 528 |
+
a2778
|
| 529 |
+
a2779
|
| 530 |
+
a2780
|
| 531 |
+
a2781
|
| 532 |
+
a2782
|
| 533 |
+
a2783
|
| 534 |
+
a2784
|
| 535 |
+
a2785
|
| 536 |
+
a2786
|
| 537 |
+
a2787
|
| 538 |
+
a2788
|
| 539 |
+
a2789
|
| 540 |
+
a2790
|
| 541 |
+
a2791
|
| 542 |
+
a2792
|
| 543 |
+
a2793
|
| 544 |
+
a2794
|
| 545 |
+
a2795
|
| 546 |
+
a2796
|
| 547 |
+
a2797
|
| 548 |
+
a2798
|
| 549 |
+
a2799
|
| 550 |
+
a2800
|
| 551 |
+
a2801
|
| 552 |
+
a2802
|
| 553 |
+
a2803
|
| 554 |
+
a2804
|
| 555 |
+
a2805
|
| 556 |
+
a2806
|
| 557 |
+
a2807
|
| 558 |
+
a2808
|
| 559 |
+
a2809
|
| 560 |
+
a2810
|
| 561 |
+
a2811
|
| 562 |
+
a2812
|
| 563 |
+
a2813
|
| 564 |
+
a2814
|
| 565 |
+
a2815
|
| 566 |
+
a2816
|
| 567 |
+
a2817
|
| 568 |
+
a2818
|
| 569 |
+
a2819
|
| 570 |
+
a2820
|
| 571 |
+
a2821
|
| 572 |
+
a2822
|
| 573 |
+
a2823
|
| 574 |
+
a2824
|
| 575 |
+
a2825
|
| 576 |
+
a2826
|
| 577 |
+
a2827
|
| 578 |
+
a2828
|
| 579 |
+
a2829
|
| 580 |
+
a2830
|
| 581 |
+
a2831
|
| 582 |
+
a2832
|
| 583 |
+
a2833
|
| 584 |
+
a2834
|
| 585 |
+
a2835
|
| 586 |
+
a2836
|
| 587 |
+
a2837
|
| 588 |
+
a2838
|
| 589 |
+
a2839
|
| 590 |
+
a2840
|
| 591 |
+
a2841
|
| 592 |
+
a2842
|
| 593 |
+
a2843
|
| 594 |
+
a2844
|
| 595 |
+
a2845
|
| 596 |
+
a2846
|
| 597 |
+
a2847
|
| 598 |
+
a2848
|
| 599 |
+
a2849
|
| 600 |
+
a2850
|
| 601 |
+
a2851
|
| 602 |
+
a2852
|
| 603 |
+
a2853
|
| 604 |
+
a2854
|
| 605 |
+
a2855
|
| 606 |
+
a2856
|
| 607 |
+
a2857
|
| 608 |
+
a2858
|
| 609 |
+
a2859
|
| 610 |
+
a2860
|
| 611 |
+
a2861
|
| 612 |
+
a2862
|
| 613 |
+
a2863
|
| 614 |
+
a2864
|
| 615 |
+
a2865
|
| 616 |
+
a2866
|
| 617 |
+
a2867
|
| 618 |
+
a2868
|
| 619 |
+
a2869
|
| 620 |
+
a2870
|
| 621 |
+
a2871
|
| 622 |
+
a2872
|
| 623 |
+
a2873
|
| 624 |
+
a2874
|
| 625 |
+
a2875
|
| 626 |
+
a2876
|
| 627 |
+
a2877
|
| 628 |
+
a2878
|
| 629 |
+
a2879
|
| 630 |
+
a2880
|
| 631 |
+
a2881
|
| 632 |
+
a2882
|
| 633 |
+
a2883
|
| 634 |
+
a2884
|
| 635 |
+
a2885
|
| 636 |
+
a2886
|
| 637 |
+
a2887
|
| 638 |
+
a2888
|
| 639 |
+
a2889
|
| 640 |
+
a2890
|
| 641 |
+
a2891
|
| 642 |
+
a2892
|
| 643 |
+
a2893
|
| 644 |
+
a2894
|
| 645 |
+
a2895
|
| 646 |
+
a2896
|
| 647 |
+
a2897
|
| 648 |
+
a2898
|
| 649 |
+
a2899
|
| 650 |
+
a2900
|
| 651 |
+
a2901
|
| 652 |
+
a2902
|
| 653 |
+
a2903
|
| 654 |
+
a2904
|
| 655 |
+
a2905
|
| 656 |
+
a2906
|
| 657 |
+
a2907
|
| 658 |
+
a2908
|
| 659 |
+
a2909
|
| 660 |
+
a2910
|
| 661 |
+
a2911
|
| 662 |
+
a2912
|
| 663 |
+
a2913
|
| 664 |
+
a2914
|
| 665 |
+
a2915
|
| 666 |
+
a2916
|
| 667 |
+
a2917
|
| 668 |
+
a2918
|
| 669 |
+
a2919
|
| 670 |
+
a2920
|
| 671 |
+
a2921
|
| 672 |
+
a2922
|
| 673 |
+
a2923
|
| 674 |
+
a2924
|
| 675 |
+
a2925
|
| 676 |
+
a2926
|
| 677 |
+
a2927
|
| 678 |
+
a2928
|
| 679 |
+
a2929
|
| 680 |
+
a2930
|
| 681 |
+
a2931
|
| 682 |
+
a2932
|
| 683 |
+
a2933
|
| 684 |
+
a2934
|
| 685 |
+
a2935
|
| 686 |
+
a2936
|
| 687 |
+
a2937
|
| 688 |
+
a2938
|
| 689 |
+
a2939
|
| 690 |
+
a2940
|
| 691 |
+
a2941
|
| 692 |
+
a2942
|
| 693 |
+
a2943
|
| 694 |
+
a2944
|
| 695 |
+
a2945
|
| 696 |
+
a2946
|
| 697 |
+
a2947
|
| 698 |
+
a2948
|
| 699 |
+
a2949
|
| 700 |
+
a2950
|
| 701 |
+
a2951
|
| 702 |
+
a2952
|
| 703 |
+
a2953
|
| 704 |
+
a2954
|
| 705 |
+
a2955
|
| 706 |
+
a2956
|
| 707 |
+
a2957
|
| 708 |
+
a2958
|
| 709 |
+
a2959
|
| 710 |
+
a2960
|
| 711 |
+
a2961
|
| 712 |
+
a2962
|
| 713 |
+
a2963
|
| 714 |
+
a2964
|
| 715 |
+
a2965
|
| 716 |
+
a2966
|
| 717 |
+
a2967
|
| 718 |
+
a2968
|
| 719 |
+
a2969
|
| 720 |
+
a2970
|
| 721 |
+
a2971
|
| 722 |
+
a2972
|
| 723 |
+
a2973
|
| 724 |
+
a2974
|
| 725 |
+
a2975
|
| 726 |
+
a2976
|
| 727 |
+
a2977
|
| 728 |
+
a2978
|
| 729 |
+
a2979
|
| 730 |
+
a2980
|
| 731 |
+
a2981
|
| 732 |
+
a2982
|
| 733 |
+
a2983
|
| 734 |
+
a2984
|
| 735 |
+
a2985
|
| 736 |
+
a2986
|
| 737 |
+
a2987
|
| 738 |
+
a2988
|
| 739 |
+
a2989
|
| 740 |
+
a2990
|
| 741 |
+
a2991
|
| 742 |
+
a2992
|
| 743 |
+
a2993
|
| 744 |
+
a2994
|
| 745 |
+
a2995
|
| 746 |
+
a2996
|
| 747 |
+
a2997
|
| 748 |
+
a2998
|
| 749 |
+
a2999
|
| 750 |
+
a3000
|
| 751 |
+
a3001
|
| 752 |
+
a3002
|
| 753 |
+
a3003
|
| 754 |
+
a3004
|
| 755 |
+
a3005
|
| 756 |
+
a3006
|
| 757 |
+
a3007
|
| 758 |
+
a3008
|
| 759 |
+
a3009
|
| 760 |
+
a3010
|
| 761 |
+
a3011
|
| 762 |
+
a3012
|
| 763 |
+
a3013
|
| 764 |
+
a3014
|
| 765 |
+
a3015
|
| 766 |
+
a3016
|
| 767 |
+
a3017
|
| 768 |
+
a3018
|
| 769 |
+
a3019
|
| 770 |
+
a3020
|
| 771 |
+
a3021
|
| 772 |
+
a3022
|
| 773 |
+
a3023
|
| 774 |
+
a3024
|
| 775 |
+
a3025
|
| 776 |
+
a3026
|
| 777 |
+
a3027
|
| 778 |
+
a3028
|
| 779 |
+
a3029
|
| 780 |
+
a3030
|
| 781 |
+
a3031
|
| 782 |
+
a3032
|
| 783 |
+
a3033
|
| 784 |
+
a3034
|
| 785 |
+
a3035
|
| 786 |
+
a3036
|
| 787 |
+
a3037
|
| 788 |
+
a3038
|
| 789 |
+
a3039
|
| 790 |
+
a3040
|
| 791 |
+
a3041
|
| 792 |
+
a3042
|
| 793 |
+
a3043
|
| 794 |
+
a3044
|
| 795 |
+
a3045
|
| 796 |
+
a3046
|
| 797 |
+
a3047
|
| 798 |
+
a3048
|
| 799 |
+
a3049
|
| 800 |
+
a3050
|
| 801 |
+
a3051
|
| 802 |
+
a3052
|
| 803 |
+
a3053
|
| 804 |
+
a3054
|
| 805 |
+
a3055
|
| 806 |
+
a3056
|
| 807 |
+
a3057
|
| 808 |
+
a3058
|
| 809 |
+
a3059
|
| 810 |
+
a3060
|
| 811 |
+
a3061
|
| 812 |
+
a3062
|
| 813 |
+
a3063
|
| 814 |
+
a3064
|
| 815 |
+
a3065
|
| 816 |
+
a3066
|
| 817 |
+
a3067
|
| 818 |
+
a3068
|
| 819 |
+
a3069
|
| 820 |
+
a3070
|
| 821 |
+
a3071
|
| 822 |
+
a3072
|
| 823 |
+
a3073
|
| 824 |
+
a3074
|
| 825 |
+
a3075
|
| 826 |
+
a3076
|
| 827 |
+
a3077
|
| 828 |
+
a3078
|
| 829 |
+
a3079
|
| 830 |
+
a3080
|
| 831 |
+
a3081
|
| 832 |
+
a3082
|
| 833 |
+
a3083
|
| 834 |
+
a3084
|
| 835 |
+
a3085
|
| 836 |
+
a3086
|
| 837 |
+
a3087
|
| 838 |
+
a3088
|
| 839 |
+
a3089
|
| 840 |
+
a3090
|
| 841 |
+
a3091
|
| 842 |
+
a3092
|
| 843 |
+
a3093
|
| 844 |
+
a3094
|
| 845 |
+
a3095
|
| 846 |
+
a3096
|
| 847 |
+
a3097
|
| 848 |
+
a3098
|
| 849 |
+
a3099
|
| 850 |
+
a3100
|
| 851 |
+
a3101
|
| 852 |
+
a3102
|
| 853 |
+
a3103
|
| 854 |
+
a3104
|
| 855 |
+
a3105
|
| 856 |
+
a3106
|
| 857 |
+
a3107
|
| 858 |
+
a3108
|
| 859 |
+
a3109
|
| 860 |
+
a3110
|
| 861 |
+
a3111
|
| 862 |
+
a3112
|
| 863 |
+
a3113
|
| 864 |
+
a3114
|
| 865 |
+
a3115
|
| 866 |
+
a3116
|
| 867 |
+
a3117
|
| 868 |
+
a3118
|
| 869 |
+
a3119
|
| 870 |
+
a3120
|
| 871 |
+
a3121
|
| 872 |
+
a3122
|
| 873 |
+
a3123
|
| 874 |
+
a3124
|
| 875 |
+
a3125
|
| 876 |
+
a3126
|
| 877 |
+
a3127
|
| 878 |
+
a3128
|
| 879 |
+
a3129
|
| 880 |
+
a3130
|
| 881 |
+
a3131
|
| 882 |
+
a3132
|
| 883 |
+
a3133
|
| 884 |
+
a3134
|
| 885 |
+
a3135
|
| 886 |
+
a3136
|
| 887 |
+
a3137
|
| 888 |
+
a3138
|
| 889 |
+
a3139
|
| 890 |
+
a3140
|
| 891 |
+
a3141
|
| 892 |
+
a3142
|
| 893 |
+
a3143
|
| 894 |
+
a3144
|
| 895 |
+
a3145
|
| 896 |
+
a3146
|
| 897 |
+
a3147
|
| 898 |
+
a3148
|
| 899 |
+
a3149
|
| 900 |
+
a3150
|
| 901 |
+
a3151
|
| 902 |
+
a3152
|
| 903 |
+
a3153
|
| 904 |
+
a3154
|
| 905 |
+
a3155
|
| 906 |
+
a3156
|
| 907 |
+
a3157
|
| 908 |
+
a3158
|
| 909 |
+
a3159
|
| 910 |
+
a3160
|
| 911 |
+
a3161
|
| 912 |
+
a3162
|
| 913 |
+
a3163
|
| 914 |
+
a3164
|
| 915 |
+
a3165
|
| 916 |
+
a3166
|
| 917 |
+
a3167
|
| 918 |
+
a3168
|
| 919 |
+
a3169
|
| 920 |
+
a3170
|
| 921 |
+
a3171
|
| 922 |
+
a3172
|
| 923 |
+
a3173
|
| 924 |
+
a3174
|
| 925 |
+
a3175
|
| 926 |
+
a3176
|
| 927 |
+
a3177
|
| 928 |
+
a3178
|
| 929 |
+
a3179
|
| 930 |
+
a3180
|
| 931 |
+
a3181
|
| 932 |
+
a3182
|
| 933 |
+
a3183
|
| 934 |
+
a3184
|
| 935 |
+
a3185
|
| 936 |
+
a3186
|
| 937 |
+
a3187
|
| 938 |
+
a3188
|
| 939 |
+
a3189
|
| 940 |
+
a3190
|
| 941 |
+
a3191
|
| 942 |
+
a3192
|
| 943 |
+
a3193
|
| 944 |
+
a3194
|
| 945 |
+
a3195
|
| 946 |
+
a3196
|
| 947 |
+
a3197
|
| 948 |
+
a3198
|
| 949 |
+
a3199
|
| 950 |
+
a3200
|
| 951 |
+
a3201
|
| 952 |
+
a3202
|
| 953 |
+
a3203
|
| 954 |
+
a3204
|
| 955 |
+
a3205
|
| 956 |
+
a3206
|
| 957 |
+
a3207
|
| 958 |
+
a3208
|
| 959 |
+
a3209
|
| 960 |
+
a3210
|
| 961 |
+
a3211
|
| 962 |
+
a3212
|
| 963 |
+
a3213
|
| 964 |
+
a3214
|
| 965 |
+
a3215
|
| 966 |
+
a3216
|
| 967 |
+
a3217
|
| 968 |
+
a3218
|
| 969 |
+
a3219
|
| 970 |
+
a3220
|
| 971 |
+
a3221
|
| 972 |
+
a3222
|
| 973 |
+
a3223
|
| 974 |
+
a3224
|
| 975 |
+
a3225
|
| 976 |
+
a3226
|
| 977 |
+
a3227
|
| 978 |
+
a3228
|
| 979 |
+
a3229
|
| 980 |
+
a3230
|
| 981 |
+
a3231
|
| 982 |
+
a3232
|
| 983 |
+
a3233
|
| 984 |
+
a3234
|
| 985 |
+
a3235
|
| 986 |
+
a3236
|
| 987 |
+
a3237
|
| 988 |
+
a3238
|
| 989 |
+
a3239
|
| 990 |
+
a3240
|
| 991 |
+
a3241
|
| 992 |
+
a3242
|
| 993 |
+
a3243
|
| 994 |
+
a3244
|
| 995 |
+
a3245
|
| 996 |
+
a3246
|
| 997 |
+
a3247
|
| 998 |
+
a3248
|
| 999 |
+
a3249
|
| 1000 |
+
a3250
|
| 1001 |
+
a3251
|
| 1002 |
+
a3252
|
| 1003 |
+
a3253
|
| 1004 |
+
a3254
|
| 1005 |
+
a3255
|
| 1006 |
+
a3256
|
| 1007 |
+
a3257
|
| 1008 |
+
a3258
|
| 1009 |
+
a3259
|
| 1010 |
+
a3260
|
| 1011 |
+
a3261
|
| 1012 |
+
a3262
|
| 1013 |
+
a3263
|
| 1014 |
+
a3264
|
| 1015 |
+
a3265
|
| 1016 |
+
a3266
|
| 1017 |
+
a3267
|
| 1018 |
+
a3268
|
| 1019 |
+
a3269
|
| 1020 |
+
a3270
|
| 1021 |
+
a3271
|
| 1022 |
+
a3272
|
| 1023 |
+
a3273
|
| 1024 |
+
a3274
|
| 1025 |
+
a3275
|
| 1026 |
+
a3276
|
| 1027 |
+
a3277
|
| 1028 |
+
a3278
|
| 1029 |
+
a3279
|
| 1030 |
+
a3280
|
| 1031 |
+
a3281
|
| 1032 |
+
a3282
|
| 1033 |
+
a3283
|
| 1034 |
+
a3284
|
| 1035 |
+
a3285
|
| 1036 |
+
a3286
|
| 1037 |
+
a3287
|
| 1038 |
+
a3288
|
| 1039 |
+
a3289
|
| 1040 |
+
a3290
|
| 1041 |
+
a3291
|
| 1042 |
+
a3292
|
| 1043 |
+
a3293
|
| 1044 |
+
a3294
|
| 1045 |
+
a3295
|
| 1046 |
+
a3296
|
| 1047 |
+
a3297
|
| 1048 |
+
a3298
|
| 1049 |
+
a3299
|
| 1050 |
+
a3300
|
| 1051 |
+
a3301
|
| 1052 |
+
a3302
|
| 1053 |
+
a3303
|
| 1054 |
+
a3304
|
| 1055 |
+
a3305
|
| 1056 |
+
a3306
|
| 1057 |
+
a3307
|
| 1058 |
+
a3308
|
| 1059 |
+
a3309
|
| 1060 |
+
a3310
|
| 1061 |
+
a3311
|
| 1062 |
+
a3312
|
| 1063 |
+
a3313
|
| 1064 |
+
a3314
|
| 1065 |
+
a3315
|
| 1066 |
+
a3316
|
| 1067 |
+
a3317
|
| 1068 |
+
a3318
|
| 1069 |
+
a3319
|
| 1070 |
+
a3320
|
| 1071 |
+
a3321
|
| 1072 |
+
a3322
|
| 1073 |
+
a3323
|
| 1074 |
+
a3324
|
| 1075 |
+
a3325
|
| 1076 |
+
a3326
|
| 1077 |
+
a3327
|
| 1078 |
+
a3328
|
| 1079 |
+
a3329
|
| 1080 |
+
a3330
|
| 1081 |
+
a3331
|
| 1082 |
+
a3332
|
| 1083 |
+
a3333
|
| 1084 |
+
a3334
|
| 1085 |
+
a3335
|
| 1086 |
+
a3336
|
| 1087 |
+
a3337
|
| 1088 |
+
a3338
|
| 1089 |
+
a3339
|
| 1090 |
+
a3340
|
| 1091 |
+
a3341
|
| 1092 |
+
a3342
|
| 1093 |
+
a3343
|
| 1094 |
+
a3344
|
| 1095 |
+
a3345
|
| 1096 |
+
a3346
|
| 1097 |
+
a3347
|
| 1098 |
+
a3348
|
| 1099 |
+
a3349
|
| 1100 |
+
a3350
|
| 1101 |
+
a3351
|
| 1102 |
+
a3352
|
| 1103 |
+
a3353
|
| 1104 |
+
a3354
|
| 1105 |
+
a3355
|
| 1106 |
+
a3356
|
| 1107 |
+
a3357
|
| 1108 |
+
a3358
|
| 1109 |
+
a3359
|
| 1110 |
+
a3360
|
| 1111 |
+
a3361
|
| 1112 |
+
a3362
|
| 1113 |
+
a3363
|
| 1114 |
+
a3364
|
| 1115 |
+
a3365
|
| 1116 |
+
a3366
|
| 1117 |
+
a3367
|
| 1118 |
+
a3368
|
| 1119 |
+
a3369
|
| 1120 |
+
a3370
|
| 1121 |
+
a3371
|
| 1122 |
+
a3372
|
| 1123 |
+
a3373
|
| 1124 |
+
a3374
|
| 1125 |
+
a3375
|
| 1126 |
+
a3376
|
| 1127 |
+
a3377
|
| 1128 |
+
a3378
|
| 1129 |
+
a3379
|
| 1130 |
+
a3380
|
| 1131 |
+
a3381
|
| 1132 |
+
a3382
|
| 1133 |
+
a3383
|
| 1134 |
+
a3384
|
| 1135 |
+
a3385
|
| 1136 |
+
a3386
|
| 1137 |
+
a3387
|
| 1138 |
+
a3388
|
| 1139 |
+
a3389
|
| 1140 |
+
a3390
|
| 1141 |
+
a3391
|
| 1142 |
+
a3392
|
| 1143 |
+
a3393
|
| 1144 |
+
a3394
|
| 1145 |
+
a3395
|
| 1146 |
+
a3396
|
| 1147 |
+
a3397
|
| 1148 |
+
a3398
|
| 1149 |
+
a3399
|
| 1150 |
+
a3400
|
| 1151 |
+
a3401
|
| 1152 |
+
a3402
|
| 1153 |
+
a3403
|
| 1154 |
+
a3404
|
| 1155 |
+
a3405
|
| 1156 |
+
a3406
|
| 1157 |
+
a3407
|
| 1158 |
+
a3408
|
| 1159 |
+
a3409
|
| 1160 |
+
a3410
|
| 1161 |
+
a3411
|
| 1162 |
+
a3412
|
| 1163 |
+
a3413
|
| 1164 |
+
a3414
|
| 1165 |
+
a3415
|
| 1166 |
+
a3416
|
| 1167 |
+
a3417
|
| 1168 |
+
a3418
|
| 1169 |
+
a3419
|
| 1170 |
+
a3420
|
| 1171 |
+
a3421
|
| 1172 |
+
a3422
|
| 1173 |
+
a3423
|
| 1174 |
+
a3424
|
| 1175 |
+
a3425
|
| 1176 |
+
a3426
|
| 1177 |
+
a3427
|
| 1178 |
+
a3428
|
| 1179 |
+
a3429
|
| 1180 |
+
a3430
|
| 1181 |
+
a3431
|
| 1182 |
+
a3432
|
| 1183 |
+
a3433
|
| 1184 |
+
a3434
|
| 1185 |
+
a3435
|
| 1186 |
+
a3436
|
| 1187 |
+
a3437
|
| 1188 |
+
a3438
|
| 1189 |
+
a3439
|
| 1190 |
+
a3440
|
| 1191 |
+
a3441
|
| 1192 |
+
a3442
|
| 1193 |
+
a3443
|
| 1194 |
+
a3444
|
| 1195 |
+
a3445
|
| 1196 |
+
a3446
|
| 1197 |
+
a3447
|
| 1198 |
+
a3448
|
| 1199 |
+
a3449
|
| 1200 |
+
a3450
|
| 1201 |
+
a3451
|
| 1202 |
+
a3452
|
| 1203 |
+
a3453
|
| 1204 |
+
a3454
|
| 1205 |
+
a3455
|
| 1206 |
+
a3456
|
| 1207 |
+
a3457
|
| 1208 |
+
a3458
|
| 1209 |
+
a3459
|
| 1210 |
+
a3460
|
| 1211 |
+
a3461
|
| 1212 |
+
a3462
|
| 1213 |
+
a3463
|
| 1214 |
+
a3464
|
| 1215 |
+
a3465
|
| 1216 |
+
a3466
|
| 1217 |
+
a3467
|
| 1218 |
+
a3468
|
| 1219 |
+
a3469
|
| 1220 |
+
a3470
|
| 1221 |
+
a3471
|
| 1222 |
+
a3472
|
| 1223 |
+
a3473
|
| 1224 |
+
a3474
|
| 1225 |
+
a3475
|
| 1226 |
+
a3476
|
| 1227 |
+
a3477
|
| 1228 |
+
a3478
|
| 1229 |
+
a3479
|
| 1230 |
+
a3480
|
| 1231 |
+
a3481
|
| 1232 |
+
a3482
|
| 1233 |
+
a3483
|
| 1234 |
+
a3484
|
| 1235 |
+
a3485
|
| 1236 |
+
a3486
|
| 1237 |
+
a3487
|
| 1238 |
+
a3488
|
| 1239 |
+
a3489
|
| 1240 |
+
a3490
|
| 1241 |
+
a3491
|
| 1242 |
+
a3492
|
| 1243 |
+
a3493
|
| 1244 |
+
a3494
|
| 1245 |
+
a3495
|
| 1246 |
+
a3496
|
| 1247 |
+
a3497
|
| 1248 |
+
a3498
|
| 1249 |
+
a3499
|
| 1250 |
+
a3500
|
| 1251 |
+
a3501
|
| 1252 |
+
a3502
|
| 1253 |
+
a3503
|
| 1254 |
+
a3504
|
| 1255 |
+
a3505
|
| 1256 |
+
a3506
|
| 1257 |
+
a3507
|
| 1258 |
+
a3508
|
| 1259 |
+
a3509
|
| 1260 |
+
a3510
|
| 1261 |
+
a3511
|
| 1262 |
+
a3512
|
| 1263 |
+
a3513
|
| 1264 |
+
a3514
|
| 1265 |
+
a3515
|
| 1266 |
+
a3516
|
| 1267 |
+
a3517
|
| 1268 |
+
a3518
|
| 1269 |
+
a3519
|
| 1270 |
+
a3520
|
| 1271 |
+
a3521
|
| 1272 |
+
a3522
|
| 1273 |
+
a3523
|
| 1274 |
+
a3524
|
| 1275 |
+
a3525
|
| 1276 |
+
a3526
|
| 1277 |
+
a3527
|
| 1278 |
+
a3528
|
| 1279 |
+
a3529
|
| 1280 |
+
a3530
|
| 1281 |
+
a3531
|
| 1282 |
+
a3532
|
| 1283 |
+
a3533
|
| 1284 |
+
a3534
|
| 1285 |
+
a3535
|
| 1286 |
+
a3536
|
| 1287 |
+
a3537
|
| 1288 |
+
a3538
|
| 1289 |
+
a3539
|
| 1290 |
+
a3540
|
| 1291 |
+
a3541
|
| 1292 |
+
a3542
|
| 1293 |
+
a3543
|
| 1294 |
+
a3544
|
| 1295 |
+
a3545
|
| 1296 |
+
a3546
|
| 1297 |
+
a3547
|
| 1298 |
+
a3548
|
| 1299 |
+
a3549
|
| 1300 |
+
a3550
|
| 1301 |
+
a3551
|
| 1302 |
+
a3552
|
| 1303 |
+
a3553
|
| 1304 |
+
a3554
|
| 1305 |
+
a3555
|
| 1306 |
+
a3556
|
| 1307 |
+
a3557
|
| 1308 |
+
a3558
|
| 1309 |
+
a3559
|
| 1310 |
+
a3560
|
| 1311 |
+
a3561
|
| 1312 |
+
a3562
|
| 1313 |
+
a3563
|
| 1314 |
+
a3564
|
| 1315 |
+
a3565
|
| 1316 |
+
a3566
|
| 1317 |
+
a3567
|
| 1318 |
+
a3568
|
| 1319 |
+
a3569
|
| 1320 |
+
a3570
|
| 1321 |
+
a3571
|
| 1322 |
+
a3572
|
| 1323 |
+
a3573
|
| 1324 |
+
a3574
|
| 1325 |
+
a3575
|
| 1326 |
+
a3576
|
| 1327 |
+
a3577
|
| 1328 |
+
a3578
|
| 1329 |
+
a3579
|
| 1330 |
+
a3580
|
| 1331 |
+
a3581
|
| 1332 |
+
a3582
|
| 1333 |
+
a3583
|
| 1334 |
+
a3584
|
| 1335 |
+
a3585
|
| 1336 |
+
a3586
|
| 1337 |
+
a3587
|
| 1338 |
+
a3588
|
| 1339 |
+
a3589
|
| 1340 |
+
a3590
|
| 1341 |
+
a3591
|
| 1342 |
+
a3592
|
| 1343 |
+
a3593
|
| 1344 |
+
a3594
|
| 1345 |
+
a3595
|
| 1346 |
+
a3596
|
| 1347 |
+
a3597
|
| 1348 |
+
a3598
|
| 1349 |
+
a3599
|
| 1350 |
+
a3600
|
| 1351 |
+
a3601
|
| 1352 |
+
a3602
|
| 1353 |
+
a3603
|
| 1354 |
+
a3604
|
| 1355 |
+
a3605
|
| 1356 |
+
a3606
|
| 1357 |
+
a3607
|
| 1358 |
+
a3608
|
| 1359 |
+
a3609
|
| 1360 |
+
a3610
|
| 1361 |
+
a3611
|
| 1362 |
+
a3612
|
| 1363 |
+
a3613
|
| 1364 |
+
a3614
|
| 1365 |
+
a3615
|
| 1366 |
+
a3616
|
| 1367 |
+
a3617
|
| 1368 |
+
a3618
|
| 1369 |
+
a3619
|
| 1370 |
+
a3620
|
| 1371 |
+
a3621
|
| 1372 |
+
a3622
|
| 1373 |
+
a3623
|
| 1374 |
+
a3624
|
| 1375 |
+
a3625
|
| 1376 |
+
a3626
|
| 1377 |
+
a3627
|
| 1378 |
+
a3628
|
| 1379 |
+
a3629
|
| 1380 |
+
a3630
|
| 1381 |
+
a3631
|
| 1382 |
+
a3632
|
| 1383 |
+
a3633
|
| 1384 |
+
a3634
|
| 1385 |
+
a3635
|
| 1386 |
+
a3636
|
| 1387 |
+
a3637
|
| 1388 |
+
a3638
|
| 1389 |
+
a3639
|
| 1390 |
+
a3640
|
| 1391 |
+
a3641
|
| 1392 |
+
a3642
|
| 1393 |
+
a3643
|
| 1394 |
+
a3644
|
| 1395 |
+
a3645
|
| 1396 |
+
a3646
|
| 1397 |
+
a3647
|
| 1398 |
+
a3648
|
| 1399 |
+
a3649
|
| 1400 |
+
a3650
|
| 1401 |
+
a3651
|
| 1402 |
+
a3652
|
| 1403 |
+
a3653
|
| 1404 |
+
a3654
|
| 1405 |
+
a3655
|
| 1406 |
+
a3656
|
| 1407 |
+
a3657
|
| 1408 |
+
a3658
|
| 1409 |
+
a3659
|
| 1410 |
+
a3660
|
| 1411 |
+
a3661
|
| 1412 |
+
a3662
|
| 1413 |
+
a3663
|
| 1414 |
+
a3664
|
| 1415 |
+
a3665
|
| 1416 |
+
a3666
|
| 1417 |
+
a3667
|
| 1418 |
+
a3668
|
| 1419 |
+
a3669
|
| 1420 |
+
a3670
|
| 1421 |
+
a3671
|
| 1422 |
+
a3672
|
| 1423 |
+
a3673
|
| 1424 |
+
a3674
|
| 1425 |
+
a3675
|
| 1426 |
+
a3676
|
| 1427 |
+
a3677
|
| 1428 |
+
a3678
|
| 1429 |
+
a3679
|
| 1430 |
+
a3680
|
| 1431 |
+
a3681
|
| 1432 |
+
a3682
|
| 1433 |
+
a3683
|
| 1434 |
+
a3684
|
| 1435 |
+
a3685
|
| 1436 |
+
a3686
|
| 1437 |
+
a3687
|
| 1438 |
+
a3688
|
| 1439 |
+
a3689
|
| 1440 |
+
a3690
|
| 1441 |
+
a3691
|
| 1442 |
+
a3692
|
| 1443 |
+
a3693
|
| 1444 |
+
a3694
|
| 1445 |
+
a3695
|
| 1446 |
+
a3696
|
| 1447 |
+
a3697
|
| 1448 |
+
a3698
|
| 1449 |
+
a3699
|
| 1450 |
+
a3700
|
| 1451 |
+
a3701
|
| 1452 |
+
a3702
|
| 1453 |
+
a3703
|
| 1454 |
+
a3704
|
| 1455 |
+
a3705
|
| 1456 |
+
a3706
|
| 1457 |
+
a3707
|
| 1458 |
+
a3708
|
| 1459 |
+
a3709
|
| 1460 |
+
a3710
|
| 1461 |
+
a3711
|
| 1462 |
+
a3712
|
| 1463 |
+
a3713
|
| 1464 |
+
a3714
|
| 1465 |
+
a3715
|
| 1466 |
+
a3716
|
| 1467 |
+
a3717
|
| 1468 |
+
a3718
|
| 1469 |
+
a3719
|
| 1470 |
+
a3720
|
| 1471 |
+
a3721
|
| 1472 |
+
a3722
|
| 1473 |
+
a3723
|
| 1474 |
+
a3724
|
| 1475 |
+
a3725
|
| 1476 |
+
a3726
|
| 1477 |
+
a3727
|
| 1478 |
+
a3728
|
| 1479 |
+
a3729
|
| 1480 |
+
a3730
|
| 1481 |
+
a3731
|
| 1482 |
+
a3732
|
| 1483 |
+
a3733
|
| 1484 |
+
a3734
|
| 1485 |
+
a3735
|
| 1486 |
+
a3736
|
| 1487 |
+
a3737
|
| 1488 |
+
a3738
|
| 1489 |
+
a3739
|
| 1490 |
+
a3740
|
| 1491 |
+
a3741
|
| 1492 |
+
a3742
|
| 1493 |
+
a3743
|
| 1494 |
+
a3744
|
| 1495 |
+
a3745
|
| 1496 |
+
a3746
|
| 1497 |
+
a3747
|
| 1498 |
+
a3748
|
| 1499 |
+
a3749
|
| 1500 |
+
a3750
|
| 1501 |
+
a3751
|
| 1502 |
+
a3752
|
| 1503 |
+
a3753
|
| 1504 |
+
a3754
|
| 1505 |
+
a3755
|
| 1506 |
+
a3756
|
| 1507 |
+
a3757
|
| 1508 |
+
a3758
|
| 1509 |
+
a3759
|
| 1510 |
+
a3760
|
| 1511 |
+
a3761
|
| 1512 |
+
a3762
|
| 1513 |
+
a3763
|
| 1514 |
+
a3764
|
| 1515 |
+
a3765
|
| 1516 |
+
a3766
|
| 1517 |
+
a3767
|
| 1518 |
+
a3768
|
| 1519 |
+
a3769
|
| 1520 |
+
a3770
|
| 1521 |
+
a3771
|
| 1522 |
+
a3772
|
| 1523 |
+
a3773
|
| 1524 |
+
a3774
|
| 1525 |
+
a3775
|
| 1526 |
+
a3776
|
| 1527 |
+
a3777
|
| 1528 |
+
a3778
|
| 1529 |
+
a3779
|
| 1530 |
+
a3780
|
| 1531 |
+
a3781
|
| 1532 |
+
a3782
|
| 1533 |
+
a3783
|
| 1534 |
+
a3784
|
| 1535 |
+
a3785
|
| 1536 |
+
a3786
|
| 1537 |
+
a3787
|
| 1538 |
+
a3788
|
| 1539 |
+
a3789
|
| 1540 |
+
a3790
|
| 1541 |
+
a3791
|
| 1542 |
+
a3792
|
| 1543 |
+
a3793
|
| 1544 |
+
a3794
|
| 1545 |
+
a3795
|
| 1546 |
+
a3796
|
| 1547 |
+
a3797
|
| 1548 |
+
a3798
|
| 1549 |
+
a3799
|
| 1550 |
+
a3800
|
| 1551 |
+
a3801
|
| 1552 |
+
a3802
|
| 1553 |
+
a3803
|
| 1554 |
+
a3804
|
| 1555 |
+
a3805
|
| 1556 |
+
a3806
|
| 1557 |
+
a3807
|
| 1558 |
+
a3808
|
| 1559 |
+
a3809
|
| 1560 |
+
a3810
|
| 1561 |
+
a3811
|
| 1562 |
+
a3812
|
| 1563 |
+
a3813
|
| 1564 |
+
a3814
|
| 1565 |
+
a3815
|
| 1566 |
+
a3816
|
| 1567 |
+
a3817
|
| 1568 |
+
a3818
|
| 1569 |
+
a3819
|
| 1570 |
+
a3820
|
| 1571 |
+
a3821
|
| 1572 |
+
a3822
|
| 1573 |
+
a3823
|
| 1574 |
+
a3824
|
| 1575 |
+
a3825
|
| 1576 |
+
a3826
|
| 1577 |
+
a3827
|
| 1578 |
+
a3828
|
| 1579 |
+
a3829
|
| 1580 |
+
a3830
|
| 1581 |
+
a3831
|
| 1582 |
+
a3832
|
| 1583 |
+
a3833
|
| 1584 |
+
a3834
|
| 1585 |
+
a3835
|
| 1586 |
+
a3836
|
| 1587 |
+
a3837
|
| 1588 |
+
a3838
|
| 1589 |
+
a3839
|
| 1590 |
+
a3840
|
| 1591 |
+
a3841
|
| 1592 |
+
a3842
|
| 1593 |
+
a3843
|
| 1594 |
+
a3844
|
| 1595 |
+
a3845
|
| 1596 |
+
a3846
|
| 1597 |
+
a3847
|
| 1598 |
+
a3848
|
| 1599 |
+
a3849
|
| 1600 |
+
a3850
|
| 1601 |
+
a3851
|
| 1602 |
+
a3852
|
| 1603 |
+
a3853
|
| 1604 |
+
a3854
|
| 1605 |
+
a3855
|
| 1606 |
+
a3856
|
| 1607 |
+
a3857
|
| 1608 |
+
a3858
|
| 1609 |
+
a3859
|
| 1610 |
+
a3860
|
| 1611 |
+
a3861
|
| 1612 |
+
a3862
|
| 1613 |
+
a3863
|
| 1614 |
+
a3864
|
| 1615 |
+
a3865
|
| 1616 |
+
a3866
|
| 1617 |
+
a3867
|
| 1618 |
+
a3868
|
| 1619 |
+
a3869
|
| 1620 |
+
a3870
|
| 1621 |
+
a3871
|
| 1622 |
+
a3872
|
| 1623 |
+
a3873
|
| 1624 |
+
a3874
|
| 1625 |
+
a3875
|
| 1626 |
+
a3876
|
| 1627 |
+
a3877
|
| 1628 |
+
a3878
|
| 1629 |
+
a3879
|
| 1630 |
+
a3880
|
| 1631 |
+
a3881
|
| 1632 |
+
a3882
|
| 1633 |
+
a3883
|
| 1634 |
+
a3884
|
| 1635 |
+
a3885
|
| 1636 |
+
a3886
|
| 1637 |
+
a3887
|
| 1638 |
+
a3888
|
| 1639 |
+
a3889
|
| 1640 |
+
a3890
|
| 1641 |
+
a3891
|
| 1642 |
+
a3892
|
| 1643 |
+
a3893
|
| 1644 |
+
a3894
|
| 1645 |
+
a3895
|
| 1646 |
+
a3896
|
| 1647 |
+
a3897
|
| 1648 |
+
a3898
|
| 1649 |
+
a3899
|
| 1650 |
+
a3900
|
| 1651 |
+
a3901
|
| 1652 |
+
a3902
|
| 1653 |
+
a3903
|
| 1654 |
+
a3904
|
| 1655 |
+
a3905
|
| 1656 |
+
a3906
|
| 1657 |
+
a3907
|
| 1658 |
+
a3908
|
| 1659 |
+
a3909
|
| 1660 |
+
a3910
|
| 1661 |
+
a3911
|
| 1662 |
+
a3912
|
| 1663 |
+
a3913
|
| 1664 |
+
a3914
|
| 1665 |
+
a3915
|
| 1666 |
+
a3916
|
| 1667 |
+
a3917
|
| 1668 |
+
a3918
|
| 1669 |
+
a3919
|
| 1670 |
+
a3920
|
| 1671 |
+
a3921
|
| 1672 |
+
a3922
|
| 1673 |
+
a3923
|
| 1674 |
+
a3924
|
| 1675 |
+
a3925
|
| 1676 |
+
a3926
|
| 1677 |
+
a3927
|
| 1678 |
+
a3928
|
| 1679 |
+
a3929
|
| 1680 |
+
a3930
|
| 1681 |
+
a3931
|
| 1682 |
+
a3932
|
| 1683 |
+
a3933
|
| 1684 |
+
a3934
|
| 1685 |
+
a3935
|
| 1686 |
+
a3936
|
| 1687 |
+
a3937
|
| 1688 |
+
a3938
|
| 1689 |
+
a3939
|
| 1690 |
+
a3940
|
| 1691 |
+
a3941
|
| 1692 |
+
a3942
|
| 1693 |
+
a3943
|
| 1694 |
+
a3944
|
| 1695 |
+
a3945
|
| 1696 |
+
a3946
|
| 1697 |
+
a3947
|
| 1698 |
+
a3948
|
| 1699 |
+
a3949
|
| 1700 |
+
a3950
|
| 1701 |
+
a3951
|
| 1702 |
+
a3952
|
| 1703 |
+
a3953
|
| 1704 |
+
a3954
|
| 1705 |
+
a3955
|
| 1706 |
+
a3956
|
| 1707 |
+
a3957
|
| 1708 |
+
a3958
|
| 1709 |
+
a3959
|
| 1710 |
+
a3960
|
| 1711 |
+
a3961
|
| 1712 |
+
a3962
|
| 1713 |
+
a3963
|
| 1714 |
+
a3964
|
| 1715 |
+
a3965
|
| 1716 |
+
a3966
|
| 1717 |
+
a3967
|
| 1718 |
+
a3968
|
| 1719 |
+
a3969
|
| 1720 |
+
a3970
|
| 1721 |
+
a3971
|
| 1722 |
+
a3972
|
| 1723 |
+
a3973
|
| 1724 |
+
a3974
|
| 1725 |
+
a3975
|
| 1726 |
+
a3976
|
| 1727 |
+
a3977
|
| 1728 |
+
a3978
|
| 1729 |
+
a3979
|
| 1730 |
+
a3980
|
| 1731 |
+
a3981
|
| 1732 |
+
a3982
|
| 1733 |
+
a3983
|
| 1734 |
+
a3984
|
| 1735 |
+
a3985
|
| 1736 |
+
a3986
|
| 1737 |
+
a3987
|
| 1738 |
+
a3988
|
| 1739 |
+
a3989
|
| 1740 |
+
a3990
|
| 1741 |
+
a3991
|
| 1742 |
+
a3992
|
| 1743 |
+
a3993
|
| 1744 |
+
a3994
|
| 1745 |
+
a3995
|
| 1746 |
+
a3996
|
| 1747 |
+
a3997
|
| 1748 |
+
a3998
|
| 1749 |
+
a3999
|
| 1750 |
+
a4000
|
| 1751 |
+
a4001
|
| 1752 |
+
a4002
|
| 1753 |
+
a4003
|
| 1754 |
+
a4004
|
| 1755 |
+
a4005
|
| 1756 |
+
a4006
|
| 1757 |
+
a4007
|
| 1758 |
+
a4008
|
| 1759 |
+
a4009
|
| 1760 |
+
a4010
|
| 1761 |
+
a4011
|
| 1762 |
+
a4012
|
| 1763 |
+
a4013
|
| 1764 |
+
a4014
|
| 1765 |
+
a4015
|
| 1766 |
+
a4016
|
| 1767 |
+
a4017
|
| 1768 |
+
a4018
|
| 1769 |
+
a4019
|
| 1770 |
+
a4020
|
| 1771 |
+
a4021
|
| 1772 |
+
a4022
|
| 1773 |
+
a4023
|
| 1774 |
+
a4024
|
| 1775 |
+
a4025
|
| 1776 |
+
a4026
|
| 1777 |
+
a4027
|
| 1778 |
+
a4028
|
| 1779 |
+
a4029
|
| 1780 |
+
a4030
|
| 1781 |
+
a4031
|
| 1782 |
+
a4032
|
| 1783 |
+
a4033
|
| 1784 |
+
a4034
|
| 1785 |
+
a4035
|
| 1786 |
+
a4036
|
| 1787 |
+
a4037
|
| 1788 |
+
a4038
|
| 1789 |
+
a4039
|
| 1790 |
+
a4040
|
| 1791 |
+
a4041
|
| 1792 |
+
a4042
|
| 1793 |
+
a4043
|
| 1794 |
+
a4044
|
| 1795 |
+
a4045
|
| 1796 |
+
a4046
|
| 1797 |
+
a4047
|
| 1798 |
+
a4048
|
| 1799 |
+
a4049
|
| 1800 |
+
a4050
|
| 1801 |
+
a4051
|
| 1802 |
+
a4052
|
| 1803 |
+
a4053
|
| 1804 |
+
a4054
|
| 1805 |
+
a4055
|
| 1806 |
+
a4056
|
| 1807 |
+
a4057
|
| 1808 |
+
a4058
|
| 1809 |
+
a4059
|
| 1810 |
+
a4060
|
| 1811 |
+
a4061
|
| 1812 |
+
a4062
|
| 1813 |
+
a4063
|
| 1814 |
+
a4064
|
| 1815 |
+
a4065
|
| 1816 |
+
a4066
|
| 1817 |
+
a4067
|
| 1818 |
+
a4068
|
| 1819 |
+
a4069
|
| 1820 |
+
a4070
|
| 1821 |
+
a4071
|
| 1822 |
+
a4072
|
| 1823 |
+
a4073
|
| 1824 |
+
a4074
|
| 1825 |
+
a4075
|
| 1826 |
+
a4076
|
| 1827 |
+
a4077
|
| 1828 |
+
a4078
|
| 1829 |
+
a4079
|
| 1830 |
+
a4080
|
| 1831 |
+
a4081
|
| 1832 |
+
a4082
|
| 1833 |
+
a4083
|
| 1834 |
+
a4084
|
| 1835 |
+
a4085
|
| 1836 |
+
a4086
|
| 1837 |
+
a4087
|
| 1838 |
+
a4088
|
| 1839 |
+
a4089
|
| 1840 |
+
a4090
|
| 1841 |
+
a4091
|
| 1842 |
+
a4092
|
| 1843 |
+
a4093
|
| 1844 |
+
a4094
|
| 1845 |
+
a4095
|
| 1846 |
+
a4096
|
| 1847 |
+
a4097
|
| 1848 |
+
a4098
|
| 1849 |
+
a4099
|
| 1850 |
+
a4100
|
| 1851 |
+
a4101
|
| 1852 |
+
a4102
|
| 1853 |
+
a4103
|
| 1854 |
+
a4104
|
| 1855 |
+
a4105
|
| 1856 |
+
a4106
|
| 1857 |
+
a4107
|
| 1858 |
+
a4108
|
| 1859 |
+
a4109
|
| 1860 |
+
a4110
|
| 1861 |
+
a4111
|
| 1862 |
+
a4112
|
| 1863 |
+
a4113
|
| 1864 |
+
a4114
|
| 1865 |
+
a4115
|
| 1866 |
+
a4116
|
| 1867 |
+
a4117
|
| 1868 |
+
a4118
|
| 1869 |
+
a4119
|
| 1870 |
+
a4120
|
| 1871 |
+
a4121
|
| 1872 |
+
a4122
|
| 1873 |
+
a4123
|
| 1874 |
+
a4124
|
| 1875 |
+
a4125
|
| 1876 |
+
a4126
|
| 1877 |
+
a4127
|
| 1878 |
+
a4128
|
| 1879 |
+
a4129
|
| 1880 |
+
a4130
|
| 1881 |
+
a4131
|
| 1882 |
+
a4132
|
| 1883 |
+
a4133
|
| 1884 |
+
a4134
|
| 1885 |
+
a4135
|
| 1886 |
+
a4136
|
| 1887 |
+
a4137
|
| 1888 |
+
a4138
|
| 1889 |
+
a4139
|
| 1890 |
+
a4140
|
| 1891 |
+
a4141
|
| 1892 |
+
a4142
|
| 1893 |
+
a4143
|
| 1894 |
+
a4144
|
| 1895 |
+
a4145
|
| 1896 |
+
a4146
|
| 1897 |
+
a4147
|
| 1898 |
+
a4148
|
| 1899 |
+
a4149
|
| 1900 |
+
a4150
|
| 1901 |
+
a4151
|
| 1902 |
+
a4152
|
| 1903 |
+
a4153
|
| 1904 |
+
a4154
|
| 1905 |
+
a4155
|
| 1906 |
+
a4156
|
| 1907 |
+
a4157
|
| 1908 |
+
a4158
|
| 1909 |
+
a4159
|
| 1910 |
+
a4160
|
| 1911 |
+
a4161
|
| 1912 |
+
a4162
|
| 1913 |
+
a4163
|
| 1914 |
+
a4164
|
| 1915 |
+
a4165
|
| 1916 |
+
a4166
|
| 1917 |
+
a4167
|
| 1918 |
+
a4168
|
| 1919 |
+
a4169
|
| 1920 |
+
a4170
|
| 1921 |
+
a4171
|
| 1922 |
+
a4172
|
| 1923 |
+
a4173
|
| 1924 |
+
a4174
|
| 1925 |
+
a4175
|
| 1926 |
+
a4176
|
| 1927 |
+
a4177
|
| 1928 |
+
a4178
|
| 1929 |
+
a4179
|
| 1930 |
+
a4180
|
| 1931 |
+
a4181
|
| 1932 |
+
a4182
|
| 1933 |
+
a4183
|
| 1934 |
+
a4184
|
| 1935 |
+
a4185
|
| 1936 |
+
a4186
|
| 1937 |
+
a4187
|
| 1938 |
+
a4188
|
| 1939 |
+
a4189
|
| 1940 |
+
a4190
|
| 1941 |
+
a4191
|
| 1942 |
+
a4192
|
| 1943 |
+
a4193
|
| 1944 |
+
a4194
|
| 1945 |
+
a4195
|
| 1946 |
+
a4196
|
| 1947 |
+
a4197
|
| 1948 |
+
a4198
|
| 1949 |
+
a4199
|
| 1950 |
+
a4200
|
| 1951 |
+
a4201
|
| 1952 |
+
a4202
|
| 1953 |
+
a4203
|
| 1954 |
+
a4204
|
| 1955 |
+
a4205
|
| 1956 |
+
a4206
|
| 1957 |
+
a4207
|
| 1958 |
+
a4208
|
| 1959 |
+
a4209
|
| 1960 |
+
a4210
|
| 1961 |
+
a4211
|
| 1962 |
+
a4212
|
| 1963 |
+
a4213
|
| 1964 |
+
a4214
|
| 1965 |
+
a4215
|
| 1966 |
+
a4216
|
| 1967 |
+
a4217
|
| 1968 |
+
a4218
|
| 1969 |
+
a4219
|
| 1970 |
+
a4220
|
| 1971 |
+
a4221
|
| 1972 |
+
a4222
|
| 1973 |
+
a4223
|
| 1974 |
+
a4224
|
| 1975 |
+
a4225
|
| 1976 |
+
a4226
|
| 1977 |
+
a4227
|
| 1978 |
+
a4228
|
| 1979 |
+
a4229
|
| 1980 |
+
a4230
|
| 1981 |
+
a4231
|
| 1982 |
+
a4232
|
| 1983 |
+
a4233
|
| 1984 |
+
a4234
|
| 1985 |
+
a4235
|
| 1986 |
+
a4236
|
| 1987 |
+
a4237
|
| 1988 |
+
a4238
|
| 1989 |
+
a4239
|
| 1990 |
+
a4240
|
| 1991 |
+
a4241
|
| 1992 |
+
a4242
|
| 1993 |
+
a4243
|
| 1994 |
+
a4244
|
| 1995 |
+
a4245
|
| 1996 |
+
a4246
|
| 1997 |
+
a4247
|
| 1998 |
+
a4248
|
| 1999 |
+
a4249
|
| 2000 |
+
a4250
|
| 2001 |
+
a4251
|
| 2002 |
+
a4252
|
| 2003 |
+
a4253
|
| 2004 |
+
a4254
|
| 2005 |
+
a4255
|
| 2006 |
+
a4256
|
| 2007 |
+
a4257
|
| 2008 |
+
a4258
|
| 2009 |
+
a4259
|
| 2010 |
+
a4260
|
| 2011 |
+
a4261
|
| 2012 |
+
a4262
|
| 2013 |
+
a4263
|
| 2014 |
+
a4264
|
| 2015 |
+
a4265
|
| 2016 |
+
a4266
|
| 2017 |
+
a4267
|
| 2018 |
+
a4268
|
| 2019 |
+
a4269
|
| 2020 |
+
a4270
|
| 2021 |
+
a4271
|
| 2022 |
+
a4272
|
| 2023 |
+
a4273
|
| 2024 |
+
a4274
|
| 2025 |
+
a4275
|
| 2026 |
+
a4276
|
| 2027 |
+
a4277
|
| 2028 |
+
a4278
|
| 2029 |
+
a4279
|
| 2030 |
+
a4280
|
| 2031 |
+
a4281
|
| 2032 |
+
a4282
|
| 2033 |
+
a4283
|
| 2034 |
+
a4284
|
| 2035 |
+
a4285
|
| 2036 |
+
a4286
|
| 2037 |
+
a4287
|
| 2038 |
+
a4288
|
| 2039 |
+
a4289
|
| 2040 |
+
a4290
|
| 2041 |
+
a4291
|
| 2042 |
+
a4292
|
| 2043 |
+
a4293
|
| 2044 |
+
a4294
|
| 2045 |
+
a4295
|
| 2046 |
+
a4296
|
| 2047 |
+
a4297
|
| 2048 |
+
a4298
|
| 2049 |
+
a4299
|
| 2050 |
+
a4300
|
| 2051 |
+
a4301
|
| 2052 |
+
a4302
|
| 2053 |
+
a4303
|
| 2054 |
+
a4304
|
| 2055 |
+
a4305
|
| 2056 |
+
a4306
|
| 2057 |
+
a4307
|
| 2058 |
+
a4308
|
| 2059 |
+
a4309
|
| 2060 |
+
a4310
|
| 2061 |
+
a4311
|
| 2062 |
+
a4312
|
| 2063 |
+
a4313
|
| 2064 |
+
a4314
|
| 2065 |
+
a4315
|
| 2066 |
+
a4316
|
| 2067 |
+
a4317
|
| 2068 |
+
a4318
|
| 2069 |
+
a4319
|
| 2070 |
+
a4320
|
| 2071 |
+
a4321
|
| 2072 |
+
a4322
|
| 2073 |
+
a4323
|
| 2074 |
+
a4324
|
| 2075 |
+
a4325
|
| 2076 |
+
a4326
|
| 2077 |
+
a4327
|
| 2078 |
+
a4328
|
| 2079 |
+
a4329
|
| 2080 |
+
a4330
|
| 2081 |
+
a4331
|
| 2082 |
+
a4332
|
| 2083 |
+
a4333
|
| 2084 |
+
a4334
|
| 2085 |
+
a4335
|
| 2086 |
+
a4336
|
| 2087 |
+
a4337
|
| 2088 |
+
a4338
|
| 2089 |
+
a4339
|
| 2090 |
+
a4340
|
| 2091 |
+
a4341
|
| 2092 |
+
a4342
|
| 2093 |
+
a4343
|
| 2094 |
+
a4344
|
| 2095 |
+
a4345
|
| 2096 |
+
a4346
|
| 2097 |
+
a4347
|
| 2098 |
+
a4348
|
| 2099 |
+
a4349
|
| 2100 |
+
a4350
|
| 2101 |
+
a4351
|
| 2102 |
+
a4352
|
| 2103 |
+
a4353
|
| 2104 |
+
a4354
|
| 2105 |
+
a4355
|
| 2106 |
+
a4356
|
| 2107 |
+
a4357
|
| 2108 |
+
a4358
|
| 2109 |
+
a4359
|
| 2110 |
+
a4360
|
| 2111 |
+
a4361
|
| 2112 |
+
a4362
|
| 2113 |
+
a4363
|
| 2114 |
+
a4364
|
| 2115 |
+
a4365
|
| 2116 |
+
a4366
|
| 2117 |
+
a4367
|
| 2118 |
+
a4368
|
| 2119 |
+
a4369
|
| 2120 |
+
a4370
|
| 2121 |
+
a4371
|
| 2122 |
+
a4372
|
| 2123 |
+
a4373
|
| 2124 |
+
a4374
|
| 2125 |
+
a4375
|
| 2126 |
+
a4376
|
| 2127 |
+
a4377
|
| 2128 |
+
a4378
|
| 2129 |
+
a4379
|
| 2130 |
+
a4380
|
| 2131 |
+
a4381
|
| 2132 |
+
a4382
|
| 2133 |
+
a4383
|
| 2134 |
+
a4384
|
| 2135 |
+
a4385
|
| 2136 |
+
a4386
|
| 2137 |
+
a4387
|
| 2138 |
+
a4388
|
| 2139 |
+
a4389
|
| 2140 |
+
a4390
|
| 2141 |
+
a4391
|
| 2142 |
+
a4392
|
| 2143 |
+
a4393
|
| 2144 |
+
a4394
|
| 2145 |
+
a4395
|
| 2146 |
+
a4396
|
| 2147 |
+
a4397
|
| 2148 |
+
a4398
|
| 2149 |
+
a4399
|
| 2150 |
+
a4400
|
| 2151 |
+
a4401
|
| 2152 |
+
a4402
|
| 2153 |
+
a4403
|
| 2154 |
+
a4404
|
| 2155 |
+
a4405
|
| 2156 |
+
a4406
|
| 2157 |
+
a4407
|
| 2158 |
+
a4408
|
| 2159 |
+
a4409
|
| 2160 |
+
a4410
|
| 2161 |
+
a4411
|
| 2162 |
+
a4412
|
| 2163 |
+
a4413
|
| 2164 |
+
a4414
|
| 2165 |
+
a4415
|
| 2166 |
+
a4416
|
| 2167 |
+
a4417
|
| 2168 |
+
a4418
|
| 2169 |
+
a4419
|
| 2170 |
+
a4420
|
| 2171 |
+
a4421
|
| 2172 |
+
a4422
|
| 2173 |
+
a4423
|
| 2174 |
+
a4424
|
| 2175 |
+
a4425
|
| 2176 |
+
a4426
|
| 2177 |
+
a4427
|
| 2178 |
+
a4428
|
| 2179 |
+
a4429
|
| 2180 |
+
a4430
|
| 2181 |
+
a4431
|
| 2182 |
+
a4432
|
| 2183 |
+
a4433
|
| 2184 |
+
a4434
|
| 2185 |
+
a4435
|
| 2186 |
+
a4436
|
| 2187 |
+
a4437
|
| 2188 |
+
a4438
|
| 2189 |
+
a4439
|
| 2190 |
+
a4440
|
| 2191 |
+
a4441
|
| 2192 |
+
a4442
|
| 2193 |
+
a4443
|
| 2194 |
+
a4444
|
| 2195 |
+
a4445
|
| 2196 |
+
a4446
|
| 2197 |
+
a4447
|
| 2198 |
+
a4448
|
| 2199 |
+
a4449
|
| 2200 |
+
a4450
|
| 2201 |
+
a4451
|
| 2202 |
+
a4452
|
| 2203 |
+
a4453
|
| 2204 |
+
a4454
|
| 2205 |
+
a4455
|
| 2206 |
+
a4456
|
| 2207 |
+
a4457
|
| 2208 |
+
a4458
|
| 2209 |
+
a4459
|
| 2210 |
+
a4460
|
| 2211 |
+
a4461
|
| 2212 |
+
a4462
|
| 2213 |
+
a4463
|
| 2214 |
+
a4464
|
| 2215 |
+
a4465
|
| 2216 |
+
a4466
|
| 2217 |
+
a4467
|
| 2218 |
+
a4468
|
| 2219 |
+
a4469
|
| 2220 |
+
a4470
|
| 2221 |
+
a4471
|
| 2222 |
+
a4472
|
| 2223 |
+
a4473
|
| 2224 |
+
a4474
|
| 2225 |
+
a4475
|
| 2226 |
+
a4476
|
| 2227 |
+
a4477
|
| 2228 |
+
a4478
|
| 2229 |
+
a4479
|
| 2230 |
+
a4480
|
| 2231 |
+
a4481
|
| 2232 |
+
a4482
|
| 2233 |
+
a4483
|
| 2234 |
+
a4484
|
| 2235 |
+
a4485
|
| 2236 |
+
a4486
|
| 2237 |
+
a4487
|
| 2238 |
+
a4488
|
| 2239 |
+
a4489
|
| 2240 |
+
a4490
|
| 2241 |
+
a4491
|
| 2242 |
+
a4492
|
| 2243 |
+
a4493
|
| 2244 |
+
a4494
|
| 2245 |
+
a4495
|
| 2246 |
+
a4496
|
| 2247 |
+
a4497
|
| 2248 |
+
a4498
|
| 2249 |
+
a4499
|
| 2250 |
+
a4500
|
mit5k_ids_filepath/upe_uegan/images_test.txt
ADDED
|
@@ -0,0 +1,500 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
a4501
|
| 2 |
+
a4502
|
| 3 |
+
a4503
|
| 4 |
+
a4504
|
| 5 |
+
a4505
|
| 6 |
+
a4506
|
| 7 |
+
a4507
|
| 8 |
+
a4508
|
| 9 |
+
a4509
|
| 10 |
+
a4510
|
| 11 |
+
a4511
|
| 12 |
+
a4512
|
| 13 |
+
a4513
|
| 14 |
+
a4514
|
| 15 |
+
a4515
|
| 16 |
+
a4516
|
| 17 |
+
a4517
|
| 18 |
+
a4518
|
| 19 |
+
a4519
|
| 20 |
+
a4520
|
| 21 |
+
a4521
|
| 22 |
+
a4522
|
| 23 |
+
a4523
|
| 24 |
+
a4524
|
| 25 |
+
a4525
|
| 26 |
+
a4526
|
| 27 |
+
a4527
|
| 28 |
+
a4528
|
| 29 |
+
a4529
|
| 30 |
+
a4530
|
| 31 |
+
a4531
|
| 32 |
+
a4532
|
| 33 |
+
a4533
|
| 34 |
+
a4534
|
| 35 |
+
a4535
|
| 36 |
+
a4536
|
| 37 |
+
a4537
|
| 38 |
+
a4538
|
| 39 |
+
a4539
|
| 40 |
+
a4540
|
| 41 |
+
a4541
|
| 42 |
+
a4542
|
| 43 |
+
a4543
|
| 44 |
+
a4544
|
| 45 |
+
a4545
|
| 46 |
+
a4546
|
| 47 |
+
a4547
|
| 48 |
+
a4548
|
| 49 |
+
a4549
|
| 50 |
+
a4550
|
| 51 |
+
a4551
|
| 52 |
+
a4552
|
| 53 |
+
a4553
|
| 54 |
+
a4554
|
| 55 |
+
a4555
|
| 56 |
+
a4556
|
| 57 |
+
a4557
|
| 58 |
+
a4558
|
| 59 |
+
a4559
|
| 60 |
+
a4560
|
| 61 |
+
a4561
|
| 62 |
+
a4562
|
| 63 |
+
a4563
|
| 64 |
+
a4564
|
| 65 |
+
a4565
|
| 66 |
+
a4566
|
| 67 |
+
a4567
|
| 68 |
+
a4568
|
| 69 |
+
a4569
|
| 70 |
+
a4570
|
| 71 |
+
a4571
|
| 72 |
+
a4572
|
| 73 |
+
a4573
|
| 74 |
+
a4574
|
| 75 |
+
a4575
|
| 76 |
+
a4576
|
| 77 |
+
a4577
|
| 78 |
+
a4578
|
| 79 |
+
a4579
|
| 80 |
+
a4580
|
| 81 |
+
a4581
|
| 82 |
+
a4582
|
| 83 |
+
a4583
|
| 84 |
+
a4584
|
| 85 |
+
a4585
|
| 86 |
+
a4586
|
| 87 |
+
a4587
|
| 88 |
+
a4588
|
| 89 |
+
a4589
|
| 90 |
+
a4590
|
| 91 |
+
a4591
|
| 92 |
+
a4592
|
| 93 |
+
a4593
|
| 94 |
+
a4594
|
| 95 |
+
a4595
|
| 96 |
+
a4596
|
| 97 |
+
a4597
|
| 98 |
+
a4598
|
| 99 |
+
a4599
|
| 100 |
+
a4600
|
| 101 |
+
a4601
|
| 102 |
+
a4602
|
| 103 |
+
a4603
|
| 104 |
+
a4604
|
| 105 |
+
a4605
|
| 106 |
+
a4606
|
| 107 |
+
a4607
|
| 108 |
+
a4608
|
| 109 |
+
a4609
|
| 110 |
+
a4610
|
| 111 |
+
a4611
|
| 112 |
+
a4612
|
| 113 |
+
a4613
|
| 114 |
+
a4614
|
| 115 |
+
a4615
|
| 116 |
+
a4616
|
| 117 |
+
a4617
|
| 118 |
+
a4618
|
| 119 |
+
a4619
|
| 120 |
+
a4620
|
| 121 |
+
a4621
|
| 122 |
+
a4622
|
| 123 |
+
a4623
|
| 124 |
+
a4624
|
| 125 |
+
a4625
|
| 126 |
+
a4626
|
| 127 |
+
a4627
|
| 128 |
+
a4628
|
| 129 |
+
a4629
|
| 130 |
+
a4630
|
| 131 |
+
a4631
|
| 132 |
+
a4632
|
| 133 |
+
a4633
|
| 134 |
+
a4634
|
| 135 |
+
a4635
|
| 136 |
+
a4636
|
| 137 |
+
a4637
|
| 138 |
+
a4638
|
| 139 |
+
a4639
|
| 140 |
+
a4640
|
| 141 |
+
a4641
|
| 142 |
+
a4642
|
| 143 |
+
a4643
|
| 144 |
+
a4644
|
| 145 |
+
a4645
|
| 146 |
+
a4646
|
| 147 |
+
a4647
|
| 148 |
+
a4648
|
| 149 |
+
a4649
|
| 150 |
+
a4650
|
| 151 |
+
a4651
|
| 152 |
+
a4652
|
| 153 |
+
a4653
|
| 154 |
+
a4654
|
| 155 |
+
a4655
|
| 156 |
+
a4656
|
| 157 |
+
a4657
|
| 158 |
+
a4658
|
| 159 |
+
a4659
|
| 160 |
+
a4660
|
| 161 |
+
a4661
|
| 162 |
+
a4662
|
| 163 |
+
a4663
|
| 164 |
+
a4664
|
| 165 |
+
a4665
|
| 166 |
+
a4666
|
| 167 |
+
a4667
|
| 168 |
+
a4668
|
| 169 |
+
a4669
|
| 170 |
+
a4670
|
| 171 |
+
a4671
|
| 172 |
+
a4672
|
| 173 |
+
a4673
|
| 174 |
+
a4674
|
| 175 |
+
a4675
|
| 176 |
+
a4676
|
| 177 |
+
a4677
|
| 178 |
+
a4678
|
| 179 |
+
a4679
|
| 180 |
+
a4680
|
| 181 |
+
a4681
|
| 182 |
+
a4682
|
| 183 |
+
a4683
|
| 184 |
+
a4684
|
| 185 |
+
a4685
|
| 186 |
+
a4686
|
| 187 |
+
a4687
|
| 188 |
+
a4688
|
| 189 |
+
a4689
|
| 190 |
+
a4690
|
| 191 |
+
a4691
|
| 192 |
+
a4692
|
| 193 |
+
a4693
|
| 194 |
+
a4694
|
| 195 |
+
a4695
|
| 196 |
+
a4696
|
| 197 |
+
a4697
|
| 198 |
+
a4698
|
| 199 |
+
a4699
|
| 200 |
+
a4700
|
| 201 |
+
a4701
|
| 202 |
+
a4702
|
| 203 |
+
a4703
|
| 204 |
+
a4704
|
| 205 |
+
a4705
|
| 206 |
+
a4706
|
| 207 |
+
a4707
|
| 208 |
+
a4708
|
| 209 |
+
a4709
|
| 210 |
+
a4710
|
| 211 |
+
a4711
|
| 212 |
+
a4712
|
| 213 |
+
a4713
|
| 214 |
+
a4714
|
| 215 |
+
a4715
|
| 216 |
+
a4716
|
| 217 |
+
a4717
|
| 218 |
+
a4718
|
| 219 |
+
a4719
|
| 220 |
+
a4720
|
| 221 |
+
a4721
|
| 222 |
+
a4722
|
| 223 |
+
a4723
|
| 224 |
+
a4724
|
| 225 |
+
a4725
|
| 226 |
+
a4726
|
| 227 |
+
a4727
|
| 228 |
+
a4728
|
| 229 |
+
a4729
|
| 230 |
+
a4730
|
| 231 |
+
a4731
|
| 232 |
+
a4732
|
| 233 |
+
a4733
|
| 234 |
+
a4734
|
| 235 |
+
a4735
|
| 236 |
+
a4736
|
| 237 |
+
a4737
|
| 238 |
+
a4738
|
| 239 |
+
a4739
|
| 240 |
+
a4740
|
| 241 |
+
a4741
|
| 242 |
+
a4742
|
| 243 |
+
a4743
|
| 244 |
+
a4744
|
| 245 |
+
a4745
|
| 246 |
+
a4746
|
| 247 |
+
a4747
|
| 248 |
+
a4748
|
| 249 |
+
a4749
|
| 250 |
+
a4750
|
| 251 |
+
a4751
|
| 252 |
+
a4752
|
| 253 |
+
a4753
|
| 254 |
+
a4754
|
| 255 |
+
a4755
|
| 256 |
+
a4756
|
| 257 |
+
a4757
|
| 258 |
+
a4758
|
| 259 |
+
a4759
|
| 260 |
+
a4760
|
| 261 |
+
a4761
|
| 262 |
+
a4762
|
| 263 |
+
a4763
|
| 264 |
+
a4764
|
| 265 |
+
a4765
|
| 266 |
+
a4766
|
| 267 |
+
a4767
|
| 268 |
+
a4768
|
| 269 |
+
a4769
|
| 270 |
+
a4770
|
| 271 |
+
a4771
|
| 272 |
+
a4772
|
| 273 |
+
a4773
|
| 274 |
+
a4774
|
| 275 |
+
a4775
|
| 276 |
+
a4776
|
| 277 |
+
a4777
|
| 278 |
+
a4778
|
| 279 |
+
a4779
|
| 280 |
+
a4780
|
| 281 |
+
a4781
|
| 282 |
+
a4782
|
| 283 |
+
a4783
|
| 284 |
+
a4784
|
| 285 |
+
a4785
|
| 286 |
+
a4786
|
| 287 |
+
a4787
|
| 288 |
+
a4788
|
| 289 |
+
a4789
|
| 290 |
+
a4790
|
| 291 |
+
a4791
|
| 292 |
+
a4792
|
| 293 |
+
a4793
|
| 294 |
+
a4794
|
| 295 |
+
a4795
|
| 296 |
+
a4796
|
| 297 |
+
a4797
|
| 298 |
+
a4798
|
| 299 |
+
a4799
|
| 300 |
+
a4800
|
| 301 |
+
a4801
|
| 302 |
+
a4802
|
| 303 |
+
a4803
|
| 304 |
+
a4804
|
| 305 |
+
a4805
|
| 306 |
+
a4806
|
| 307 |
+
a4807
|
| 308 |
+
a4808
|
| 309 |
+
a4809
|
| 310 |
+
a4810
|
| 311 |
+
a4811
|
| 312 |
+
a4812
|
| 313 |
+
a4813
|
| 314 |
+
a4814
|
| 315 |
+
a4815
|
| 316 |
+
a4816
|
| 317 |
+
a4817
|
| 318 |
+
a4818
|
| 319 |
+
a4819
|
| 320 |
+
a4820
|
| 321 |
+
a4821
|
| 322 |
+
a4822
|
| 323 |
+
a4823
|
| 324 |
+
a4824
|
| 325 |
+
a4825
|
| 326 |
+
a4826
|
| 327 |
+
a4827
|
| 328 |
+
a4828
|
| 329 |
+
a4829
|
| 330 |
+
a4830
|
| 331 |
+
a4831
|
| 332 |
+
a4832
|
| 333 |
+
a4833
|
| 334 |
+
a4834
|
| 335 |
+
a4835
|
| 336 |
+
a4836
|
| 337 |
+
a4837
|
| 338 |
+
a4838
|
| 339 |
+
a4839
|
| 340 |
+
a4840
|
| 341 |
+
a4841
|
| 342 |
+
a4842
|
| 343 |
+
a4843
|
| 344 |
+
a4844
|
| 345 |
+
a4845
|
| 346 |
+
a4846
|
| 347 |
+
a4847
|
| 348 |
+
a4848
|
| 349 |
+
a4849
|
| 350 |
+
a4850
|
| 351 |
+
a4851
|
| 352 |
+
a4852
|
| 353 |
+
a4853
|
| 354 |
+
a4854
|
| 355 |
+
a4855
|
| 356 |
+
a4856
|
| 357 |
+
a4857
|
| 358 |
+
a4858
|
| 359 |
+
a4859
|
| 360 |
+
a4860
|
| 361 |
+
a4861
|
| 362 |
+
a4862
|
| 363 |
+
a4863
|
| 364 |
+
a4864
|
| 365 |
+
a4865
|
| 366 |
+
a4866
|
| 367 |
+
a4867
|
| 368 |
+
a4868
|
| 369 |
+
a4869
|
| 370 |
+
a4870
|
| 371 |
+
a4871
|
| 372 |
+
a4872
|
| 373 |
+
a4873
|
| 374 |
+
a4874
|
| 375 |
+
a4875
|
| 376 |
+
a4876
|
| 377 |
+
a4877
|
| 378 |
+
a4878
|
| 379 |
+
a4879
|
| 380 |
+
a4880
|
| 381 |
+
a4881
|
| 382 |
+
a4882
|
| 383 |
+
a4883
|
| 384 |
+
a4884
|
| 385 |
+
a4885
|
| 386 |
+
a4886
|
| 387 |
+
a4887
|
| 388 |
+
a4888
|
| 389 |
+
a4889
|
| 390 |
+
a4890
|
| 391 |
+
a4891
|
| 392 |
+
a4892
|
| 393 |
+
a4893
|
| 394 |
+
a4894
|
| 395 |
+
a4895
|
| 396 |
+
a4896
|
| 397 |
+
a4897
|
| 398 |
+
a4898
|
| 399 |
+
a4899
|
| 400 |
+
a4900
|
| 401 |
+
a4901
|
| 402 |
+
a4902
|
| 403 |
+
a4903
|
| 404 |
+
a4904
|
| 405 |
+
a4905
|
| 406 |
+
a4906
|
| 407 |
+
a4907
|
| 408 |
+
a4908
|
| 409 |
+
a4909
|
| 410 |
+
a4910
|
| 411 |
+
a4911
|
| 412 |
+
a4912
|
| 413 |
+
a4913
|
| 414 |
+
a4914
|
| 415 |
+
a4915
|
| 416 |
+
a4916
|
| 417 |
+
a4917
|
| 418 |
+
a4918
|
| 419 |
+
a4919
|
| 420 |
+
a4920
|
| 421 |
+
a4921
|
| 422 |
+
a4922
|
| 423 |
+
a4923
|
| 424 |
+
a4924
|
| 425 |
+
a4925
|
| 426 |
+
a4926
|
| 427 |
+
a4927
|
| 428 |
+
a4928
|
| 429 |
+
a4929
|
| 430 |
+
a4930
|
| 431 |
+
a4931
|
| 432 |
+
a4932
|
| 433 |
+
a4933
|
| 434 |
+
a4934
|
| 435 |
+
a4935
|
| 436 |
+
a4936
|
| 437 |
+
a4937
|
| 438 |
+
a4938
|
| 439 |
+
a4939
|
| 440 |
+
a4940
|
| 441 |
+
a4941
|
| 442 |
+
a4942
|
| 443 |
+
a4943
|
| 444 |
+
a4944
|
| 445 |
+
a4945
|
| 446 |
+
a4946
|
| 447 |
+
a4947
|
| 448 |
+
a4948
|
| 449 |
+
a4949
|
| 450 |
+
a4950
|
| 451 |
+
a4951
|
| 452 |
+
a4952
|
| 453 |
+
a4953
|
| 454 |
+
a4954
|
| 455 |
+
a4955
|
| 456 |
+
a4956
|
| 457 |
+
a4957
|
| 458 |
+
a4958
|
| 459 |
+
a4959
|
| 460 |
+
a4960
|
| 461 |
+
a4961
|
| 462 |
+
a4962
|
| 463 |
+
a4963
|
| 464 |
+
a4964
|
| 465 |
+
a4965
|
| 466 |
+
a4966
|
| 467 |
+
a4967
|
| 468 |
+
a4968
|
| 469 |
+
a4969
|
| 470 |
+
a4970
|
| 471 |
+
a4971
|
| 472 |
+
a4972
|
| 473 |
+
a4973
|
| 474 |
+
a4974
|
| 475 |
+
a4975
|
| 476 |
+
a4976
|
| 477 |
+
a4977
|
| 478 |
+
a4978
|
| 479 |
+
a4979
|
| 480 |
+
a4980
|
| 481 |
+
a4981
|
| 482 |
+
a4982
|
| 483 |
+
a4983
|
| 484 |
+
a4984
|
| 485 |
+
a4985
|
| 486 |
+
a4986
|
| 487 |
+
a4987
|
| 488 |
+
a4988
|
| 489 |
+
a4989
|
| 490 |
+
a4990
|
| 491 |
+
a4991
|
| 492 |
+
a4992
|
| 493 |
+
a4993
|
| 494 |
+
a4994
|
| 495 |
+
a4995
|
| 496 |
+
a4996
|
| 497 |
+
a4997
|
| 498 |
+
a4998
|
| 499 |
+
a4999
|
| 500 |
+
a5000
|
mit5k_ids_filepath/upe_uegan/images_train.txt
ADDED
|
@@ -0,0 +1,4500 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
a0001
|
| 2 |
+
a0002
|
| 3 |
+
a0003
|
| 4 |
+
a0004
|
| 5 |
+
a0005
|
| 6 |
+
a0006
|
| 7 |
+
a0007
|
| 8 |
+
a0008
|
| 9 |
+
a0009
|
| 10 |
+
a0010
|
| 11 |
+
a0011
|
| 12 |
+
a0012
|
| 13 |
+
a0013
|
| 14 |
+
a0014
|
| 15 |
+
a0015
|
| 16 |
+
a0016
|
| 17 |
+
a0017
|
| 18 |
+
a0018
|
| 19 |
+
a0019
|
| 20 |
+
a0020
|
| 21 |
+
a0021
|
| 22 |
+
a0022
|
| 23 |
+
a0023
|
| 24 |
+
a0024
|
| 25 |
+
a0025
|
| 26 |
+
a0026
|
| 27 |
+
a0027
|
| 28 |
+
a0028
|
| 29 |
+
a0029
|
| 30 |
+
a0030
|
| 31 |
+
a0031
|
| 32 |
+
a0032
|
| 33 |
+
a0033
|
| 34 |
+
a0034
|
| 35 |
+
a0035
|
| 36 |
+
a0036
|
| 37 |
+
a0037
|
| 38 |
+
a0038
|
| 39 |
+
a0039
|
| 40 |
+
a0040
|
| 41 |
+
a0041
|
| 42 |
+
a0042
|
| 43 |
+
a0043
|
| 44 |
+
a0044
|
| 45 |
+
a0045
|
| 46 |
+
a0046
|
| 47 |
+
a0047
|
| 48 |
+
a0048
|
| 49 |
+
a0049
|
| 50 |
+
a0050
|
| 51 |
+
a0051
|
| 52 |
+
a0052
|
| 53 |
+
a0053
|
| 54 |
+
a0054
|
| 55 |
+
a0055
|
| 56 |
+
a0056
|
| 57 |
+
a0057
|
| 58 |
+
a0058
|
| 59 |
+
a0059
|
| 60 |
+
a0060
|
| 61 |
+
a0061
|
| 62 |
+
a0062
|
| 63 |
+
a0063
|
| 64 |
+
a0064
|
| 65 |
+
a0065
|
| 66 |
+
a0066
|
| 67 |
+
a0067
|
| 68 |
+
a0068
|
| 69 |
+
a0069
|
| 70 |
+
a0070
|
| 71 |
+
a0071
|
| 72 |
+
a0072
|
| 73 |
+
a0073
|
| 74 |
+
a0074
|
| 75 |
+
a0075
|
| 76 |
+
a0076
|
| 77 |
+
a0077
|
| 78 |
+
a0078
|
| 79 |
+
a0079
|
| 80 |
+
a0080
|
| 81 |
+
a0081
|
| 82 |
+
a0082
|
| 83 |
+
a0083
|
| 84 |
+
a0084
|
| 85 |
+
a0085
|
| 86 |
+
a0086
|
| 87 |
+
a0087
|
| 88 |
+
a0088
|
| 89 |
+
a0089
|
| 90 |
+
a0090
|
| 91 |
+
a0091
|
| 92 |
+
a0092
|
| 93 |
+
a0093
|
| 94 |
+
a0094
|
| 95 |
+
a0095
|
| 96 |
+
a0096
|
| 97 |
+
a0097
|
| 98 |
+
a0098
|
| 99 |
+
a0099
|
| 100 |
+
a0100
|
| 101 |
+
a0101
|
| 102 |
+
a0102
|
| 103 |
+
a0103
|
| 104 |
+
a0104
|
| 105 |
+
a0105
|
| 106 |
+
a0106
|
| 107 |
+
a0107
|
| 108 |
+
a0108
|
| 109 |
+
a0109
|
| 110 |
+
a0110
|
| 111 |
+
a0111
|
| 112 |
+
a0112
|
| 113 |
+
a0113
|
| 114 |
+
a0114
|
| 115 |
+
a0115
|
| 116 |
+
a0116
|
| 117 |
+
a0117
|
| 118 |
+
a0118
|
| 119 |
+
a0119
|
| 120 |
+
a0120
|
| 121 |
+
a0121
|
| 122 |
+
a0122
|
| 123 |
+
a0123
|
| 124 |
+
a0124
|
| 125 |
+
a0125
|
| 126 |
+
a0126
|
| 127 |
+
a0127
|
| 128 |
+
a0128
|
| 129 |
+
a0129
|
| 130 |
+
a0130
|
| 131 |
+
a0131
|
| 132 |
+
a0132
|
| 133 |
+
a0133
|
| 134 |
+
a0134
|
| 135 |
+
a0135
|
| 136 |
+
a0136
|
| 137 |
+
a0137
|
| 138 |
+
a0138
|
| 139 |
+
a0139
|
| 140 |
+
a0140
|
| 141 |
+
a0141
|
| 142 |
+
a0142
|
| 143 |
+
a0143
|
| 144 |
+
a0144
|
| 145 |
+
a0145
|
| 146 |
+
a0146
|
| 147 |
+
a0147
|
| 148 |
+
a0148
|
| 149 |
+
a0149
|
| 150 |
+
a0150
|
| 151 |
+
a0151
|
| 152 |
+
a0152
|
| 153 |
+
a0153
|
| 154 |
+
a0154
|
| 155 |
+
a0155
|
| 156 |
+
a0156
|
| 157 |
+
a0157
|
| 158 |
+
a0158
|
| 159 |
+
a0159
|
| 160 |
+
a0160
|
| 161 |
+
a0161
|
| 162 |
+
a0162
|
| 163 |
+
a0163
|
| 164 |
+
a0164
|
| 165 |
+
a0165
|
| 166 |
+
a0166
|
| 167 |
+
a0167
|
| 168 |
+
a0168
|
| 169 |
+
a0169
|
| 170 |
+
a0170
|
| 171 |
+
a0171
|
| 172 |
+
a0172
|
| 173 |
+
a0173
|
| 174 |
+
a0174
|
| 175 |
+
a0175
|
| 176 |
+
a0176
|
| 177 |
+
a0177
|
| 178 |
+
a0178
|
| 179 |
+
a0179
|
| 180 |
+
a0180
|
| 181 |
+
a0181
|
| 182 |
+
a0182
|
| 183 |
+
a0183
|
| 184 |
+
a0184
|
| 185 |
+
a0185
|
| 186 |
+
a0186
|
| 187 |
+
a0187
|
| 188 |
+
a0188
|
| 189 |
+
a0189
|
| 190 |
+
a0190
|
| 191 |
+
a0191
|
| 192 |
+
a0192
|
| 193 |
+
a0193
|
| 194 |
+
a0194
|
| 195 |
+
a0195
|
| 196 |
+
a0196
|
| 197 |
+
a0197
|
| 198 |
+
a0198
|
| 199 |
+
a0199
|
| 200 |
+
a0200
|
| 201 |
+
a0201
|
| 202 |
+
a0202
|
| 203 |
+
a0203
|
| 204 |
+
a0204
|
| 205 |
+
a0205
|
| 206 |
+
a0206
|
| 207 |
+
a0207
|
| 208 |
+
a0208
|
| 209 |
+
a0209
|
| 210 |
+
a0210
|
| 211 |
+
a0211
|
| 212 |
+
a0212
|
| 213 |
+
a0213
|
| 214 |
+
a0214
|
| 215 |
+
a0215
|
| 216 |
+
a0216
|
| 217 |
+
a0217
|
| 218 |
+
a0218
|
| 219 |
+
a0219
|
| 220 |
+
a0220
|
| 221 |
+
a0221
|
| 222 |
+
a0222
|
| 223 |
+
a0223
|
| 224 |
+
a0224
|
| 225 |
+
a0225
|
| 226 |
+
a0226
|
| 227 |
+
a0227
|
| 228 |
+
a0228
|
| 229 |
+
a0229
|
| 230 |
+
a0230
|
| 231 |
+
a0231
|
| 232 |
+
a0232
|
| 233 |
+
a0233
|
| 234 |
+
a0234
|
| 235 |
+
a0235
|
| 236 |
+
a0236
|
| 237 |
+
a0237
|
| 238 |
+
a0238
|
| 239 |
+
a0239
|
| 240 |
+
a0240
|
| 241 |
+
a0241
|
| 242 |
+
a0242
|
| 243 |
+
a0243
|
| 244 |
+
a0244
|
| 245 |
+
a0245
|
| 246 |
+
a0246
|
| 247 |
+
a0247
|
| 248 |
+
a0248
|
| 249 |
+
a0249
|
| 250 |
+
a0250
|
| 251 |
+
a0251
|
| 252 |
+
a0252
|
| 253 |
+
a0253
|
| 254 |
+
a0254
|
| 255 |
+
a0255
|
| 256 |
+
a0256
|
| 257 |
+
a0257
|
| 258 |
+
a0258
|
| 259 |
+
a0259
|
| 260 |
+
a0260
|
| 261 |
+
a0261
|
| 262 |
+
a0262
|
| 263 |
+
a0263
|
| 264 |
+
a0264
|
| 265 |
+
a0265
|
| 266 |
+
a0266
|
| 267 |
+
a0267
|
| 268 |
+
a0268
|
| 269 |
+
a0269
|
| 270 |
+
a0270
|
| 271 |
+
a0271
|
| 272 |
+
a0272
|
| 273 |
+
a0273
|
| 274 |
+
a0274
|
| 275 |
+
a0275
|
| 276 |
+
a0276
|
| 277 |
+
a0277
|
| 278 |
+
a0278
|
| 279 |
+
a0279
|
| 280 |
+
a0280
|
| 281 |
+
a0281
|
| 282 |
+
a0282
|
| 283 |
+
a0283
|
| 284 |
+
a0284
|
| 285 |
+
a0285
|
| 286 |
+
a0286
|
| 287 |
+
a0287
|
| 288 |
+
a0288
|
| 289 |
+
a0289
|
| 290 |
+
a0290
|
| 291 |
+
a0291
|
| 292 |
+
a0292
|
| 293 |
+
a0293
|
| 294 |
+
a0294
|
| 295 |
+
a0295
|
| 296 |
+
a0296
|
| 297 |
+
a0297
|
| 298 |
+
a0298
|
| 299 |
+
a0299
|
| 300 |
+
a0300
|
| 301 |
+
a0301
|
| 302 |
+
a0302
|
| 303 |
+
a0303
|
| 304 |
+
a0304
|
| 305 |
+
a0305
|
| 306 |
+
a0306
|
| 307 |
+
a0307
|
| 308 |
+
a0308
|
| 309 |
+
a0309
|
| 310 |
+
a0310
|
| 311 |
+
a0311
|
| 312 |
+
a0312
|
| 313 |
+
a0313
|
| 314 |
+
a0314
|
| 315 |
+
a0315
|
| 316 |
+
a0316
|
| 317 |
+
a0317
|
| 318 |
+
a0318
|
| 319 |
+
a0319
|
| 320 |
+
a0320
|
| 321 |
+
a0321
|
| 322 |
+
a0322
|
| 323 |
+
a0323
|
| 324 |
+
a0324
|
| 325 |
+
a0325
|
| 326 |
+
a0326
|
| 327 |
+
a0327
|
| 328 |
+
a0328
|
| 329 |
+
a0329
|
| 330 |
+
a0330
|
| 331 |
+
a0331
|
| 332 |
+
a0332
|
| 333 |
+
a0333
|
| 334 |
+
a0334
|
| 335 |
+
a0335
|
| 336 |
+
a0336
|
| 337 |
+
a0337
|
| 338 |
+
a0338
|
| 339 |
+
a0339
|
| 340 |
+
a0340
|
| 341 |
+
a0341
|
| 342 |
+
a0342
|
| 343 |
+
a0343
|
| 344 |
+
a0344
|
| 345 |
+
a0345
|
| 346 |
+
a0346
|
| 347 |
+
a0347
|
| 348 |
+
a0348
|
| 349 |
+
a0349
|
| 350 |
+
a0350
|
| 351 |
+
a0351
|
| 352 |
+
a0352
|
| 353 |
+
a0353
|
| 354 |
+
a0354
|
| 355 |
+
a0355
|
| 356 |
+
a0356
|
| 357 |
+
a0357
|
| 358 |
+
a0358
|
| 359 |
+
a0359
|
| 360 |
+
a0360
|
| 361 |
+
a0361
|
| 362 |
+
a0362
|
| 363 |
+
a0363
|
| 364 |
+
a0364
|
| 365 |
+
a0365
|
| 366 |
+
a0366
|
| 367 |
+
a0367
|
| 368 |
+
a0368
|
| 369 |
+
a0369
|
| 370 |
+
a0370
|
| 371 |
+
a0371
|
| 372 |
+
a0372
|
| 373 |
+
a0373
|
| 374 |
+
a0374
|
| 375 |
+
a0375
|
| 376 |
+
a0376
|
| 377 |
+
a0377
|
| 378 |
+
a0378
|
| 379 |
+
a0379
|
| 380 |
+
a0380
|
| 381 |
+
a0381
|
| 382 |
+
a0382
|
| 383 |
+
a0383
|
| 384 |
+
a0384
|
| 385 |
+
a0385
|
| 386 |
+
a0386
|
| 387 |
+
a0387
|
| 388 |
+
a0388
|
| 389 |
+
a0389
|
| 390 |
+
a0390
|
| 391 |
+
a0391
|
| 392 |
+
a0392
|
| 393 |
+
a0393
|
| 394 |
+
a0394
|
| 395 |
+
a0395
|
| 396 |
+
a0396
|
| 397 |
+
a0397
|
| 398 |
+
a0398
|
| 399 |
+
a0399
|
| 400 |
+
a0400
|
| 401 |
+
a0401
|
| 402 |
+
a0402
|
| 403 |
+
a0403
|
| 404 |
+
a0404
|
| 405 |
+
a0405
|
| 406 |
+
a0406
|
| 407 |
+
a0407
|
| 408 |
+
a0408
|
| 409 |
+
a0409
|
| 410 |
+
a0410
|
| 411 |
+
a0411
|
| 412 |
+
a0412
|
| 413 |
+
a0413
|
| 414 |
+
a0414
|
| 415 |
+
a0415
|
| 416 |
+
a0416
|
| 417 |
+
a0417
|
| 418 |
+
a0418
|
| 419 |
+
a0419
|
| 420 |
+
a0420
|
| 421 |
+
a0421
|
| 422 |
+
a0422
|
| 423 |
+
a0423
|
| 424 |
+
a0424
|
| 425 |
+
a0425
|
| 426 |
+
a0426
|
| 427 |
+
a0427
|
| 428 |
+
a0428
|
| 429 |
+
a0429
|
| 430 |
+
a0430
|
| 431 |
+
a0431
|
| 432 |
+
a0432
|
| 433 |
+
a0433
|
| 434 |
+
a0434
|
| 435 |
+
a0435
|
| 436 |
+
a0436
|
| 437 |
+
a0437
|
| 438 |
+
a0438
|
| 439 |
+
a0439
|
| 440 |
+
a0440
|
| 441 |
+
a0441
|
| 442 |
+
a0442
|
| 443 |
+
a0443
|
| 444 |
+
a0444
|
| 445 |
+
a0445
|
| 446 |
+
a0446
|
| 447 |
+
a0447
|
| 448 |
+
a0448
|
| 449 |
+
a0449
|
| 450 |
+
a0450
|
| 451 |
+
a0451
|
| 452 |
+
a0452
|
| 453 |
+
a0453
|
| 454 |
+
a0454
|
| 455 |
+
a0455
|
| 456 |
+
a0456
|
| 457 |
+
a0457
|
| 458 |
+
a0458
|
| 459 |
+
a0459
|
| 460 |
+
a0460
|
| 461 |
+
a0461
|
| 462 |
+
a0462
|
| 463 |
+
a0463
|
| 464 |
+
a0464
|
| 465 |
+
a0465
|
| 466 |
+
a0466
|
| 467 |
+
a0467
|
| 468 |
+
a0468
|
| 469 |
+
a0469
|
| 470 |
+
a0470
|
| 471 |
+
a0471
|
| 472 |
+
a0472
|
| 473 |
+
a0473
|
| 474 |
+
a0474
|
| 475 |
+
a0475
|
| 476 |
+
a0476
|
| 477 |
+
a0477
|
| 478 |
+
a0478
|
| 479 |
+
a0479
|
| 480 |
+
a0480
|
| 481 |
+
a0481
|
| 482 |
+
a0482
|
| 483 |
+
a0483
|
| 484 |
+
a0484
|
| 485 |
+
a0485
|
| 486 |
+
a0486
|
| 487 |
+
a0487
|
| 488 |
+
a0488
|
| 489 |
+
a0489
|
| 490 |
+
a0490
|
| 491 |
+
a0491
|
| 492 |
+
a0492
|
| 493 |
+
a0493
|
| 494 |
+
a0494
|
| 495 |
+
a0495
|
| 496 |
+
a0496
|
| 497 |
+
a0497
|
| 498 |
+
a0498
|
| 499 |
+
a0499
|
| 500 |
+
a0500
|
| 501 |
+
a0501
|
| 502 |
+
a0502
|
| 503 |
+
a0503
|
| 504 |
+
a0504
|
| 505 |
+
a0505
|
| 506 |
+
a0506
|
| 507 |
+
a0507
|
| 508 |
+
a0508
|
| 509 |
+
a0509
|
| 510 |
+
a0510
|
| 511 |
+
a0511
|
| 512 |
+
a0512
|
| 513 |
+
a0513
|
| 514 |
+
a0514
|
| 515 |
+
a0515
|
| 516 |
+
a0516
|
| 517 |
+
a0517
|
| 518 |
+
a0518
|
| 519 |
+
a0519
|
| 520 |
+
a0520
|
| 521 |
+
a0521
|
| 522 |
+
a0522
|
| 523 |
+
a0523
|
| 524 |
+
a0524
|
| 525 |
+
a0525
|
| 526 |
+
a0526
|
| 527 |
+
a0527
|
| 528 |
+
a0528
|
| 529 |
+
a0529
|
| 530 |
+
a0530
|
| 531 |
+
a0531
|
| 532 |
+
a0532
|
| 533 |
+
a0533
|
| 534 |
+
a0534
|
| 535 |
+
a0535
|
| 536 |
+
a0536
|
| 537 |
+
a0537
|
| 538 |
+
a0538
|
| 539 |
+
a0539
|
| 540 |
+
a0540
|
| 541 |
+
a0541
|
| 542 |
+
a0542
|
| 543 |
+
a0543
|
| 544 |
+
a0544
|
| 545 |
+
a0545
|
| 546 |
+
a0546
|
| 547 |
+
a0547
|
| 548 |
+
a0548
|
| 549 |
+
a0549
|
| 550 |
+
a0550
|
| 551 |
+
a0551
|
| 552 |
+
a0552
|
| 553 |
+
a0553
|
| 554 |
+
a0554
|
| 555 |
+
a0555
|
| 556 |
+
a0556
|
| 557 |
+
a0557
|
| 558 |
+
a0558
|
| 559 |
+
a0559
|
| 560 |
+
a0560
|
| 561 |
+
a0561
|
| 562 |
+
a0562
|
| 563 |
+
a0563
|
| 564 |
+
a0564
|
| 565 |
+
a0565
|
| 566 |
+
a0566
|
| 567 |
+
a0567
|
| 568 |
+
a0568
|
| 569 |
+
a0569
|
| 570 |
+
a0570
|
| 571 |
+
a0571
|
| 572 |
+
a0572
|
| 573 |
+
a0573
|
| 574 |
+
a0574
|
| 575 |
+
a0575
|
| 576 |
+
a0576
|
| 577 |
+
a0577
|
| 578 |
+
a0578
|
| 579 |
+
a0579
|
| 580 |
+
a0580
|
| 581 |
+
a0581
|
| 582 |
+
a0582
|
| 583 |
+
a0583
|
| 584 |
+
a0584
|
| 585 |
+
a0585
|
| 586 |
+
a0586
|
| 587 |
+
a0587
|
| 588 |
+
a0588
|
| 589 |
+
a0589
|
| 590 |
+
a0590
|
| 591 |
+
a0591
|
| 592 |
+
a0592
|
| 593 |
+
a0593
|
| 594 |
+
a0594
|
| 595 |
+
a0595
|
| 596 |
+
a0596
|
| 597 |
+
a0597
|
| 598 |
+
a0598
|
| 599 |
+
a0599
|
| 600 |
+
a0600
|
| 601 |
+
a0601
|
| 602 |
+
a0602
|
| 603 |
+
a0603
|
| 604 |
+
a0604
|
| 605 |
+
a0605
|
| 606 |
+
a0606
|
| 607 |
+
a0607
|
| 608 |
+
a0608
|
| 609 |
+
a0609
|
| 610 |
+
a0610
|
| 611 |
+
a0611
|
| 612 |
+
a0612
|
| 613 |
+
a0613
|
| 614 |
+
a0614
|
| 615 |
+
a0615
|
| 616 |
+
a0616
|
| 617 |
+
a0617
|
| 618 |
+
a0618
|
| 619 |
+
a0619
|
| 620 |
+
a0620
|
| 621 |
+
a0621
|
| 622 |
+
a0622
|
| 623 |
+
a0623
|
| 624 |
+
a0624
|
| 625 |
+
a0625
|
| 626 |
+
a0626
|
| 627 |
+
a0627
|
| 628 |
+
a0628
|
| 629 |
+
a0629
|
| 630 |
+
a0630
|
| 631 |
+
a0631
|
| 632 |
+
a0632
|
| 633 |
+
a0633
|
| 634 |
+
a0634
|
| 635 |
+
a0635
|
| 636 |
+
a0636
|
| 637 |
+
a0637
|
| 638 |
+
a0638
|
| 639 |
+
a0639
|
| 640 |
+
a0640
|
| 641 |
+
a0641
|
| 642 |
+
a0642
|
| 643 |
+
a0643
|
| 644 |
+
a0644
|
| 645 |
+
a0645
|
| 646 |
+
a0646
|
| 647 |
+
a0647
|
| 648 |
+
a0648
|
| 649 |
+
a0649
|
| 650 |
+
a0650
|
| 651 |
+
a0651
|
| 652 |
+
a0652
|
| 653 |
+
a0653
|
| 654 |
+
a0654
|
| 655 |
+
a0655
|
| 656 |
+
a0656
|
| 657 |
+
a0657
|
| 658 |
+
a0658
|
| 659 |
+
a0659
|
| 660 |
+
a0660
|
| 661 |
+
a0661
|
| 662 |
+
a0662
|
| 663 |
+
a0663
|
| 664 |
+
a0664
|
| 665 |
+
a0665
|
| 666 |
+
a0666
|
| 667 |
+
a0667
|
| 668 |
+
a0668
|
| 669 |
+
a0669
|
| 670 |
+
a0670
|
| 671 |
+
a0671
|
| 672 |
+
a0672
|
| 673 |
+
a0673
|
| 674 |
+
a0674
|
| 675 |
+
a0675
|
| 676 |
+
a0676
|
| 677 |
+
a0677
|
| 678 |
+
a0678
|
| 679 |
+
a0679
|
| 680 |
+
a0680
|
| 681 |
+
a0681
|
| 682 |
+
a0682
|
| 683 |
+
a0683
|
| 684 |
+
a0684
|
| 685 |
+
a0685
|
| 686 |
+
a0686
|
| 687 |
+
a0687
|
| 688 |
+
a0688
|
| 689 |
+
a0689
|
| 690 |
+
a0690
|
| 691 |
+
a0691
|
| 692 |
+
a0692
|
| 693 |
+
a0693
|
| 694 |
+
a0694
|
| 695 |
+
a0695
|
| 696 |
+
a0696
|
| 697 |
+
a0697
|
| 698 |
+
a0698
|
| 699 |
+
a0699
|
| 700 |
+
a0700
|
| 701 |
+
a0701
|
| 702 |
+
a0702
|
| 703 |
+
a0703
|
| 704 |
+
a0704
|
| 705 |
+
a0705
|
| 706 |
+
a0706
|
| 707 |
+
a0707
|
| 708 |
+
a0708
|
| 709 |
+
a0709
|
| 710 |
+
a0710
|
| 711 |
+
a0711
|
| 712 |
+
a0712
|
| 713 |
+
a0713
|
| 714 |
+
a0714
|
| 715 |
+
a0715
|
| 716 |
+
a0716
|
| 717 |
+
a0717
|
| 718 |
+
a0718
|
| 719 |
+
a0719
|
| 720 |
+
a0720
|
| 721 |
+
a0721
|
| 722 |
+
a0722
|
| 723 |
+
a0723
|
| 724 |
+
a0724
|
| 725 |
+
a0725
|
| 726 |
+
a0726
|
| 727 |
+
a0727
|
| 728 |
+
a0728
|
| 729 |
+
a0729
|
| 730 |
+
a0730
|
| 731 |
+
a0731
|
| 732 |
+
a0732
|
| 733 |
+
a0733
|
| 734 |
+
a0734
|
| 735 |
+
a0735
|
| 736 |
+
a0736
|
| 737 |
+
a0737
|
| 738 |
+
a0738
|
| 739 |
+
a0739
|
| 740 |
+
a0740
|
| 741 |
+
a0741
|
| 742 |
+
a0742
|
| 743 |
+
a0743
|
| 744 |
+
a0744
|
| 745 |
+
a0745
|
| 746 |
+
a0746
|
| 747 |
+
a0747
|
| 748 |
+
a0748
|
| 749 |
+
a0749
|
| 750 |
+
a0750
|
| 751 |
+
a0751
|
| 752 |
+
a0752
|
| 753 |
+
a0753
|
| 754 |
+
a0754
|
| 755 |
+
a0755
|
| 756 |
+
a0756
|
| 757 |
+
a0757
|
| 758 |
+
a0758
|
| 759 |
+
a0759
|
| 760 |
+
a0760
|
| 761 |
+
a0761
|
| 762 |
+
a0762
|
| 763 |
+
a0763
|
| 764 |
+
a0764
|
| 765 |
+
a0765
|
| 766 |
+
a0766
|
| 767 |
+
a0767
|
| 768 |
+
a0768
|
| 769 |
+
a0769
|
| 770 |
+
a0770
|
| 771 |
+
a0771
|
| 772 |
+
a0772
|
| 773 |
+
a0773
|
| 774 |
+
a0774
|
| 775 |
+
a0775
|
| 776 |
+
a0776
|
| 777 |
+
a0777
|
| 778 |
+
a0778
|
| 779 |
+
a0779
|
| 780 |
+
a0780
|
| 781 |
+
a0781
|
| 782 |
+
a0782
|
| 783 |
+
a0783
|
| 784 |
+
a0784
|
| 785 |
+
a0785
|
| 786 |
+
a0786
|
| 787 |
+
a0787
|
| 788 |
+
a0788
|
| 789 |
+
a0789
|
| 790 |
+
a0790
|
| 791 |
+
a0791
|
| 792 |
+
a0792
|
| 793 |
+
a0793
|
| 794 |
+
a0794
|
| 795 |
+
a0795
|
| 796 |
+
a0796
|
| 797 |
+
a0797
|
| 798 |
+
a0798
|
| 799 |
+
a0799
|
| 800 |
+
a0800
|
| 801 |
+
a0801
|
| 802 |
+
a0802
|
| 803 |
+
a0803
|
| 804 |
+
a0804
|
| 805 |
+
a0805
|
| 806 |
+
a0806
|
| 807 |
+
a0807
|
| 808 |
+
a0808
|
| 809 |
+
a0809
|
| 810 |
+
a0810
|
| 811 |
+
a0811
|
| 812 |
+
a0812
|
| 813 |
+
a0813
|
| 814 |
+
a0814
|
| 815 |
+
a0815
|
| 816 |
+
a0816
|
| 817 |
+
a0817
|
| 818 |
+
a0818
|
| 819 |
+
a0819
|
| 820 |
+
a0820
|
| 821 |
+
a0821
|
| 822 |
+
a0822
|
| 823 |
+
a0823
|
| 824 |
+
a0824
|
| 825 |
+
a0825
|
| 826 |
+
a0826
|
| 827 |
+
a0827
|
| 828 |
+
a0828
|
| 829 |
+
a0829
|
| 830 |
+
a0830
|
| 831 |
+
a0831
|
| 832 |
+
a0832
|
| 833 |
+
a0833
|
| 834 |
+
a0834
|
| 835 |
+
a0835
|
| 836 |
+
a0836
|
| 837 |
+
a0837
|
| 838 |
+
a0838
|
| 839 |
+
a0839
|
| 840 |
+
a0840
|
| 841 |
+
a0841
|
| 842 |
+
a0842
|
| 843 |
+
a0843
|
| 844 |
+
a0844
|
| 845 |
+
a0845
|
| 846 |
+
a0846
|
| 847 |
+
a0847
|
| 848 |
+
a0848
|
| 849 |
+
a0849
|
| 850 |
+
a0850
|
| 851 |
+
a0851
|
| 852 |
+
a0852
|
| 853 |
+
a0853
|
| 854 |
+
a0854
|
| 855 |
+
a0855
|
| 856 |
+
a0856
|
| 857 |
+
a0857
|
| 858 |
+
a0858
|
| 859 |
+
a0859
|
| 860 |
+
a0860
|
| 861 |
+
a0861
|
| 862 |
+
a0862
|
| 863 |
+
a0863
|
| 864 |
+
a0864
|
| 865 |
+
a0865
|
| 866 |
+
a0866
|
| 867 |
+
a0867
|
| 868 |
+
a0868
|
| 869 |
+
a0869
|
| 870 |
+
a0870
|
| 871 |
+
a0871
|
| 872 |
+
a0872
|
| 873 |
+
a0873
|
| 874 |
+
a0874
|
| 875 |
+
a0875
|
| 876 |
+
a0876
|
| 877 |
+
a0877
|
| 878 |
+
a0878
|
| 879 |
+
a0879
|
| 880 |
+
a0880
|
| 881 |
+
a0881
|
| 882 |
+
a0882
|
| 883 |
+
a0883
|
| 884 |
+
a0884
|
| 885 |
+
a0885
|
| 886 |
+
a0886
|
| 887 |
+
a0887
|
| 888 |
+
a0888
|
| 889 |
+
a0889
|
| 890 |
+
a0890
|
| 891 |
+
a0891
|
| 892 |
+
a0892
|
| 893 |
+
a0893
|
| 894 |
+
a0894
|
| 895 |
+
a0895
|
| 896 |
+
a0896
|
| 897 |
+
a0897
|
| 898 |
+
a0898
|
| 899 |
+
a0899
|
| 900 |
+
a0900
|
| 901 |
+
a0901
|
| 902 |
+
a0902
|
| 903 |
+
a0903
|
| 904 |
+
a0904
|
| 905 |
+
a0905
|
| 906 |
+
a0906
|
| 907 |
+
a0907
|
| 908 |
+
a0908
|
| 909 |
+
a0909
|
| 910 |
+
a0910
|
| 911 |
+
a0911
|
| 912 |
+
a0912
|
| 913 |
+
a0913
|
| 914 |
+
a0914
|
| 915 |
+
a0915
|
| 916 |
+
a0916
|
| 917 |
+
a0917
|
| 918 |
+
a0918
|
| 919 |
+
a0919
|
| 920 |
+
a0920
|
| 921 |
+
a0921
|
| 922 |
+
a0922
|
| 923 |
+
a0923
|
| 924 |
+
a0924
|
| 925 |
+
a0925
|
| 926 |
+
a0926
|
| 927 |
+
a0927
|
| 928 |
+
a0928
|
| 929 |
+
a0929
|
| 930 |
+
a0930
|
| 931 |
+
a0931
|
| 932 |
+
a0932
|
| 933 |
+
a0933
|
| 934 |
+
a0934
|
| 935 |
+
a0935
|
| 936 |
+
a0936
|
| 937 |
+
a0937
|
| 938 |
+
a0938
|
| 939 |
+
a0939
|
| 940 |
+
a0940
|
| 941 |
+
a0941
|
| 942 |
+
a0942
|
| 943 |
+
a0943
|
| 944 |
+
a0944
|
| 945 |
+
a0945
|
| 946 |
+
a0946
|
| 947 |
+
a0947
|
| 948 |
+
a0948
|
| 949 |
+
a0949
|
| 950 |
+
a0950
|
| 951 |
+
a0951
|
| 952 |
+
a0952
|
| 953 |
+
a0953
|
| 954 |
+
a0954
|
| 955 |
+
a0955
|
| 956 |
+
a0956
|
| 957 |
+
a0957
|
| 958 |
+
a0958
|
| 959 |
+
a0959
|
| 960 |
+
a0960
|
| 961 |
+
a0961
|
| 962 |
+
a0962
|
| 963 |
+
a0963
|
| 964 |
+
a0964
|
| 965 |
+
a0965
|
| 966 |
+
a0966
|
| 967 |
+
a0967
|
| 968 |
+
a0968
|
| 969 |
+
a0969
|
| 970 |
+
a0970
|
| 971 |
+
a0971
|
| 972 |
+
a0972
|
| 973 |
+
a0973
|
| 974 |
+
a0974
|
| 975 |
+
a0975
|
| 976 |
+
a0976
|
| 977 |
+
a0977
|
| 978 |
+
a0978
|
| 979 |
+
a0979
|
| 980 |
+
a0980
|
| 981 |
+
a0981
|
| 982 |
+
a0982
|
| 983 |
+
a0983
|
| 984 |
+
a0984
|
| 985 |
+
a0985
|
| 986 |
+
a0986
|
| 987 |
+
a0987
|
| 988 |
+
a0988
|
| 989 |
+
a0989
|
| 990 |
+
a0990
|
| 991 |
+
a0991
|
| 992 |
+
a0992
|
| 993 |
+
a0993
|
| 994 |
+
a0994
|
| 995 |
+
a0995
|
| 996 |
+
a0996
|
| 997 |
+
a0997
|
| 998 |
+
a0998
|
| 999 |
+
a0999
|
| 1000 |
+
a1000
|
| 1001 |
+
a1001
|
| 1002 |
+
a1002
|
| 1003 |
+
a1003
|
| 1004 |
+
a1004
|
| 1005 |
+
a1005
|
| 1006 |
+
a1006
|
| 1007 |
+
a1007
|
| 1008 |
+
a1008
|
| 1009 |
+
a1009
|
| 1010 |
+
a1010
|
| 1011 |
+
a1011
|
| 1012 |
+
a1012
|
| 1013 |
+
a1013
|
| 1014 |
+
a1014
|
| 1015 |
+
a1015
|
| 1016 |
+
a1016
|
| 1017 |
+
a1017
|
| 1018 |
+
a1018
|
| 1019 |
+
a1019
|
| 1020 |
+
a1020
|
| 1021 |
+
a1021
|
| 1022 |
+
a1022
|
| 1023 |
+
a1023
|
| 1024 |
+
a1024
|
| 1025 |
+
a1025
|
| 1026 |
+
a1026
|
| 1027 |
+
a1027
|
| 1028 |
+
a1028
|
| 1029 |
+
a1029
|
| 1030 |
+
a1030
|
| 1031 |
+
a1031
|
| 1032 |
+
a1032
|
| 1033 |
+
a1033
|
| 1034 |
+
a1034
|
| 1035 |
+
a1035
|
| 1036 |
+
a1036
|
| 1037 |
+
a1037
|
| 1038 |
+
a1038
|
| 1039 |
+
a1039
|
| 1040 |
+
a1040
|
| 1041 |
+
a1041
|
| 1042 |
+
a1042
|
| 1043 |
+
a1043
|
| 1044 |
+
a1044
|
| 1045 |
+
a1045
|
| 1046 |
+
a1046
|
| 1047 |
+
a1047
|
| 1048 |
+
a1048
|
| 1049 |
+
a1049
|
| 1050 |
+
a1050
|
| 1051 |
+
a1051
|
| 1052 |
+
a1052
|
| 1053 |
+
a1053
|
| 1054 |
+
a1054
|
| 1055 |
+
a1055
|
| 1056 |
+
a1056
|
| 1057 |
+
a1057
|
| 1058 |
+
a1058
|
| 1059 |
+
a1059
|
| 1060 |
+
a1060
|
| 1061 |
+
a1061
|
| 1062 |
+
a1062
|
| 1063 |
+
a1063
|
| 1064 |
+
a1064
|
| 1065 |
+
a1065
|
| 1066 |
+
a1066
|
| 1067 |
+
a1067
|
| 1068 |
+
a1068
|
| 1069 |
+
a1069
|
| 1070 |
+
a1070
|
| 1071 |
+
a1071
|
| 1072 |
+
a1072
|
| 1073 |
+
a1073
|
| 1074 |
+
a1074
|
| 1075 |
+
a1075
|
| 1076 |
+
a1076
|
| 1077 |
+
a1077
|
| 1078 |
+
a1078
|
| 1079 |
+
a1079
|
| 1080 |
+
a1080
|
| 1081 |
+
a1081
|
| 1082 |
+
a1082
|
| 1083 |
+
a1083
|
| 1084 |
+
a1084
|
| 1085 |
+
a1085
|
| 1086 |
+
a1086
|
| 1087 |
+
a1087
|
| 1088 |
+
a1088
|
| 1089 |
+
a1089
|
| 1090 |
+
a1090
|
| 1091 |
+
a1091
|
| 1092 |
+
a1092
|
| 1093 |
+
a1093
|
| 1094 |
+
a1094
|
| 1095 |
+
a1095
|
| 1096 |
+
a1096
|
| 1097 |
+
a1097
|
| 1098 |
+
a1098
|
| 1099 |
+
a1099
|
| 1100 |
+
a1100
|
| 1101 |
+
a1101
|
| 1102 |
+
a1102
|
| 1103 |
+
a1103
|
| 1104 |
+
a1104
|
| 1105 |
+
a1105
|
| 1106 |
+
a1106
|
| 1107 |
+
a1107
|
| 1108 |
+
a1108
|
| 1109 |
+
a1109
|
| 1110 |
+
a1110
|
| 1111 |
+
a1111
|
| 1112 |
+
a1112
|
| 1113 |
+
a1113
|
| 1114 |
+
a1114
|
| 1115 |
+
a1115
|
| 1116 |
+
a1116
|
| 1117 |
+
a1117
|
| 1118 |
+
a1118
|
| 1119 |
+
a1119
|
| 1120 |
+
a1120
|
| 1121 |
+
a1121
|
| 1122 |
+
a1122
|
| 1123 |
+
a1123
|
| 1124 |
+
a1124
|
| 1125 |
+
a1125
|
| 1126 |
+
a1126
|
| 1127 |
+
a1127
|
| 1128 |
+
a1128
|
| 1129 |
+
a1129
|
| 1130 |
+
a1130
|
| 1131 |
+
a1131
|
| 1132 |
+
a1132
|
| 1133 |
+
a1133
|
| 1134 |
+
a1134
|
| 1135 |
+
a1135
|
| 1136 |
+
a1136
|
| 1137 |
+
a1137
|
| 1138 |
+
a1138
|
| 1139 |
+
a1139
|
| 1140 |
+
a1140
|
| 1141 |
+
a1141
|
| 1142 |
+
a1142
|
| 1143 |
+
a1143
|
| 1144 |
+
a1144
|
| 1145 |
+
a1145
|
| 1146 |
+
a1146
|
| 1147 |
+
a1147
|
| 1148 |
+
a1148
|
| 1149 |
+
a1149
|
| 1150 |
+
a1150
|
| 1151 |
+
a1151
|
| 1152 |
+
a1152
|
| 1153 |
+
a1153
|
| 1154 |
+
a1154
|
| 1155 |
+
a1155
|
| 1156 |
+
a1156
|
| 1157 |
+
a1157
|
| 1158 |
+
a1158
|
| 1159 |
+
a1159
|
| 1160 |
+
a1160
|
| 1161 |
+
a1161
|
| 1162 |
+
a1162
|
| 1163 |
+
a1163
|
| 1164 |
+
a1164
|
| 1165 |
+
a1165
|
| 1166 |
+
a1166
|
| 1167 |
+
a1167
|
| 1168 |
+
a1168
|
| 1169 |
+
a1169
|
| 1170 |
+
a1170
|
| 1171 |
+
a1171
|
| 1172 |
+
a1172
|
| 1173 |
+
a1173
|
| 1174 |
+
a1174
|
| 1175 |
+
a1175
|
| 1176 |
+
a1176
|
| 1177 |
+
a1177
|
| 1178 |
+
a1178
|
| 1179 |
+
a1179
|
| 1180 |
+
a1180
|
| 1181 |
+
a1181
|
| 1182 |
+
a1182
|
| 1183 |
+
a1183
|
| 1184 |
+
a1184
|
| 1185 |
+
a1185
|
| 1186 |
+
a1186
|
| 1187 |
+
a1187
|
| 1188 |
+
a1188
|
| 1189 |
+
a1189
|
| 1190 |
+
a1190
|
| 1191 |
+
a1191
|
| 1192 |
+
a1192
|
| 1193 |
+
a1193
|
| 1194 |
+
a1194
|
| 1195 |
+
a1195
|
| 1196 |
+
a1196
|
| 1197 |
+
a1197
|
| 1198 |
+
a1198
|
| 1199 |
+
a1199
|
| 1200 |
+
a1200
|
| 1201 |
+
a1201
|
| 1202 |
+
a1202
|
| 1203 |
+
a1203
|
| 1204 |
+
a1204
|
| 1205 |
+
a1205
|
| 1206 |
+
a1206
|
| 1207 |
+
a1207
|
| 1208 |
+
a1208
|
| 1209 |
+
a1209
|
| 1210 |
+
a1210
|
| 1211 |
+
a1211
|
| 1212 |
+
a1212
|
| 1213 |
+
a1213
|
| 1214 |
+
a1214
|
| 1215 |
+
a1215
|
| 1216 |
+
a1216
|
| 1217 |
+
a1217
|
| 1218 |
+
a1218
|
| 1219 |
+
a1219
|
| 1220 |
+
a1220
|
| 1221 |
+
a1221
|
| 1222 |
+
a1222
|
| 1223 |
+
a1223
|
| 1224 |
+
a1224
|
| 1225 |
+
a1225
|
| 1226 |
+
a1226
|
| 1227 |
+
a1227
|
| 1228 |
+
a1228
|
| 1229 |
+
a1229
|
| 1230 |
+
a1230
|
| 1231 |
+
a1231
|
| 1232 |
+
a1232
|
| 1233 |
+
a1233
|
| 1234 |
+
a1234
|
| 1235 |
+
a1235
|
| 1236 |
+
a1236
|
| 1237 |
+
a1237
|
| 1238 |
+
a1238
|
| 1239 |
+
a1239
|
| 1240 |
+
a1240
|
| 1241 |
+
a1241
|
| 1242 |
+
a1242
|
| 1243 |
+
a1243
|
| 1244 |
+
a1244
|
| 1245 |
+
a1245
|
| 1246 |
+
a1246
|
| 1247 |
+
a1247
|
| 1248 |
+
a1248
|
| 1249 |
+
a1249
|
| 1250 |
+
a1250
|
| 1251 |
+
a1251
|
| 1252 |
+
a1252
|
| 1253 |
+
a1253
|
| 1254 |
+
a1254
|
| 1255 |
+
a1255
|
| 1256 |
+
a1256
|
| 1257 |
+
a1257
|
| 1258 |
+
a1258
|
| 1259 |
+
a1259
|
| 1260 |
+
a1260
|
| 1261 |
+
a1261
|
| 1262 |
+
a1262
|
| 1263 |
+
a1263
|
| 1264 |
+
a1264
|
| 1265 |
+
a1265
|
| 1266 |
+
a1266
|
| 1267 |
+
a1267
|
| 1268 |
+
a1268
|
| 1269 |
+
a1269
|
| 1270 |
+
a1270
|
| 1271 |
+
a1271
|
| 1272 |
+
a1272
|
| 1273 |
+
a1273
|
| 1274 |
+
a1274
|
| 1275 |
+
a1275
|
| 1276 |
+
a1276
|
| 1277 |
+
a1277
|
| 1278 |
+
a1278
|
| 1279 |
+
a1279
|
| 1280 |
+
a1280
|
| 1281 |
+
a1281
|
| 1282 |
+
a1282
|
| 1283 |
+
a1283
|
| 1284 |
+
a1284
|
| 1285 |
+
a1285
|
| 1286 |
+
a1286
|
| 1287 |
+
a1287
|
| 1288 |
+
a1288
|
| 1289 |
+
a1289
|
| 1290 |
+
a1290
|
| 1291 |
+
a1291
|
| 1292 |
+
a1292
|
| 1293 |
+
a1293
|
| 1294 |
+
a1294
|
| 1295 |
+
a1295
|
| 1296 |
+
a1296
|
| 1297 |
+
a1297
|
| 1298 |
+
a1298
|
| 1299 |
+
a1299
|
| 1300 |
+
a1300
|
| 1301 |
+
a1301
|
| 1302 |
+
a1302
|
| 1303 |
+
a1303
|
| 1304 |
+
a1304
|
| 1305 |
+
a1305
|
| 1306 |
+
a1306
|
| 1307 |
+
a1307
|
| 1308 |
+
a1308
|
| 1309 |
+
a1309
|
| 1310 |
+
a1310
|
| 1311 |
+
a1311
|
| 1312 |
+
a1312
|
| 1313 |
+
a1313
|
| 1314 |
+
a1314
|
| 1315 |
+
a1315
|
| 1316 |
+
a1316
|
| 1317 |
+
a1317
|
| 1318 |
+
a1318
|
| 1319 |
+
a1319
|
| 1320 |
+
a1320
|
| 1321 |
+
a1321
|
| 1322 |
+
a1322
|
| 1323 |
+
a1323
|
| 1324 |
+
a1324
|
| 1325 |
+
a1325
|
| 1326 |
+
a1326
|
| 1327 |
+
a1327
|
| 1328 |
+
a1328
|
| 1329 |
+
a1329
|
| 1330 |
+
a1330
|
| 1331 |
+
a1331
|
| 1332 |
+
a1332
|
| 1333 |
+
a1333
|
| 1334 |
+
a1334
|
| 1335 |
+
a1335
|
| 1336 |
+
a1336
|
| 1337 |
+
a1337
|
| 1338 |
+
a1338
|
| 1339 |
+
a1339
|
| 1340 |
+
a1340
|
| 1341 |
+
a1341
|
| 1342 |
+
a1342
|
| 1343 |
+
a1343
|
| 1344 |
+
a1344
|
| 1345 |
+
a1345
|
| 1346 |
+
a1346
|
| 1347 |
+
a1347
|
| 1348 |
+
a1348
|
| 1349 |
+
a1349
|
| 1350 |
+
a1350
|
| 1351 |
+
a1351
|
| 1352 |
+
a1352
|
| 1353 |
+
a1353
|
| 1354 |
+
a1354
|
| 1355 |
+
a1355
|
| 1356 |
+
a1356
|
| 1357 |
+
a1357
|
| 1358 |
+
a1358
|
| 1359 |
+
a1359
|
| 1360 |
+
a1360
|
| 1361 |
+
a1361
|
| 1362 |
+
a1362
|
| 1363 |
+
a1363
|
| 1364 |
+
a1364
|
| 1365 |
+
a1365
|
| 1366 |
+
a1366
|
| 1367 |
+
a1367
|
| 1368 |
+
a1368
|
| 1369 |
+
a1369
|
| 1370 |
+
a1370
|
| 1371 |
+
a1371
|
| 1372 |
+
a1372
|
| 1373 |
+
a1373
|
| 1374 |
+
a1374
|
| 1375 |
+
a1375
|
| 1376 |
+
a1376
|
| 1377 |
+
a1377
|
| 1378 |
+
a1378
|
| 1379 |
+
a1379
|
| 1380 |
+
a1380
|
| 1381 |
+
a1381
|
| 1382 |
+
a1382
|
| 1383 |
+
a1383
|
| 1384 |
+
a1384
|
| 1385 |
+
a1385
|
| 1386 |
+
a1386
|
| 1387 |
+
a1387
|
| 1388 |
+
a1388
|
| 1389 |
+
a1389
|
| 1390 |
+
a1390
|
| 1391 |
+
a1391
|
| 1392 |
+
a1392
|
| 1393 |
+
a1393
|
| 1394 |
+
a1394
|
| 1395 |
+
a1395
|
| 1396 |
+
a1396
|
| 1397 |
+
a1397
|
| 1398 |
+
a1398
|
| 1399 |
+
a1399
|
| 1400 |
+
a1400
|
| 1401 |
+
a1401
|
| 1402 |
+
a1402
|
| 1403 |
+
a1403
|
| 1404 |
+
a1404
|
| 1405 |
+
a1405
|
| 1406 |
+
a1406
|
| 1407 |
+
a1407
|
| 1408 |
+
a1408
|
| 1409 |
+
a1409
|
| 1410 |
+
a1410
|
| 1411 |
+
a1411
|
| 1412 |
+
a1412
|
| 1413 |
+
a1413
|
| 1414 |
+
a1414
|
| 1415 |
+
a1415
|
| 1416 |
+
a1416
|
| 1417 |
+
a1417
|
| 1418 |
+
a1418
|
| 1419 |
+
a1419
|
| 1420 |
+
a1420
|
| 1421 |
+
a1421
|
| 1422 |
+
a1422
|
| 1423 |
+
a1423
|
| 1424 |
+
a1424
|
| 1425 |
+
a1425
|
| 1426 |
+
a1426
|
| 1427 |
+
a1427
|
| 1428 |
+
a1428
|
| 1429 |
+
a1429
|
| 1430 |
+
a1430
|
| 1431 |
+
a1431
|
| 1432 |
+
a1432
|
| 1433 |
+
a1433
|
| 1434 |
+
a1434
|
| 1435 |
+
a1435
|
| 1436 |
+
a1436
|
| 1437 |
+
a1437
|
| 1438 |
+
a1438
|
| 1439 |
+
a1439
|
| 1440 |
+
a1440
|
| 1441 |
+
a1441
|
| 1442 |
+
a1442
|
| 1443 |
+
a1443
|
| 1444 |
+
a1444
|
| 1445 |
+
a1445
|
| 1446 |
+
a1446
|
| 1447 |
+
a1447
|
| 1448 |
+
a1448
|
| 1449 |
+
a1449
|
| 1450 |
+
a1450
|
| 1451 |
+
a1451
|
| 1452 |
+
a1452
|
| 1453 |
+
a1453
|
| 1454 |
+
a1454
|
| 1455 |
+
a1455
|
| 1456 |
+
a1456
|
| 1457 |
+
a1457
|
| 1458 |
+
a1458
|
| 1459 |
+
a1459
|
| 1460 |
+
a1460
|
| 1461 |
+
a1461
|
| 1462 |
+
a1462
|
| 1463 |
+
a1463
|
| 1464 |
+
a1464
|
| 1465 |
+
a1465
|
| 1466 |
+
a1466
|
| 1467 |
+
a1467
|
| 1468 |
+
a1468
|
| 1469 |
+
a1469
|
| 1470 |
+
a1470
|
| 1471 |
+
a1471
|
| 1472 |
+
a1472
|
| 1473 |
+
a1473
|
| 1474 |
+
a1474
|
| 1475 |
+
a1475
|
| 1476 |
+
a1476
|
| 1477 |
+
a1477
|
| 1478 |
+
a1478
|
| 1479 |
+
a1479
|
| 1480 |
+
a1480
|
| 1481 |
+
a1481
|
| 1482 |
+
a1482
|
| 1483 |
+
a1483
|
| 1484 |
+
a1484
|
| 1485 |
+
a1485
|
| 1486 |
+
a1486
|
| 1487 |
+
a1487
|
| 1488 |
+
a1488
|
| 1489 |
+
a1489
|
| 1490 |
+
a1490
|
| 1491 |
+
a1491
|
| 1492 |
+
a1492
|
| 1493 |
+
a1493
|
| 1494 |
+
a1494
|
| 1495 |
+
a1495
|
| 1496 |
+
a1496
|
| 1497 |
+
a1497
|
| 1498 |
+
a1498
|
| 1499 |
+
a1499
|
| 1500 |
+
a1500
|
| 1501 |
+
a1501
|
| 1502 |
+
a1502
|
| 1503 |
+
a1503
|
| 1504 |
+
a1504
|
| 1505 |
+
a1505
|
| 1506 |
+
a1506
|
| 1507 |
+
a1507
|
| 1508 |
+
a1508
|
| 1509 |
+
a1509
|
| 1510 |
+
a1510
|
| 1511 |
+
a1511
|
| 1512 |
+
a1512
|
| 1513 |
+
a1513
|
| 1514 |
+
a1514
|
| 1515 |
+
a1515
|
| 1516 |
+
a1516
|
| 1517 |
+
a1517
|
| 1518 |
+
a1518
|
| 1519 |
+
a1519
|
| 1520 |
+
a1520
|
| 1521 |
+
a1521
|
| 1522 |
+
a1522
|
| 1523 |
+
a1523
|
| 1524 |
+
a1524
|
| 1525 |
+
a1525
|
| 1526 |
+
a1526
|
| 1527 |
+
a1527
|
| 1528 |
+
a1528
|
| 1529 |
+
a1529
|
| 1530 |
+
a1530
|
| 1531 |
+
a1531
|
| 1532 |
+
a1532
|
| 1533 |
+
a1533
|
| 1534 |
+
a1534
|
| 1535 |
+
a1535
|
| 1536 |
+
a1536
|
| 1537 |
+
a1537
|
| 1538 |
+
a1538
|
| 1539 |
+
a1539
|
| 1540 |
+
a1540
|
| 1541 |
+
a1541
|
| 1542 |
+
a1542
|
| 1543 |
+
a1543
|
| 1544 |
+
a1544
|
| 1545 |
+
a1545
|
| 1546 |
+
a1546
|
| 1547 |
+
a1547
|
| 1548 |
+
a1548
|
| 1549 |
+
a1549
|
| 1550 |
+
a1550
|
| 1551 |
+
a1551
|
| 1552 |
+
a1552
|
| 1553 |
+
a1553
|
| 1554 |
+
a1554
|
| 1555 |
+
a1555
|
| 1556 |
+
a1556
|
| 1557 |
+
a1557
|
| 1558 |
+
a1558
|
| 1559 |
+
a1559
|
| 1560 |
+
a1560
|
| 1561 |
+
a1561
|
| 1562 |
+
a1562
|
| 1563 |
+
a1563
|
| 1564 |
+
a1564
|
| 1565 |
+
a1565
|
| 1566 |
+
a1566
|
| 1567 |
+
a1567
|
| 1568 |
+
a1568
|
| 1569 |
+
a1569
|
| 1570 |
+
a1570
|
| 1571 |
+
a1571
|
| 1572 |
+
a1572
|
| 1573 |
+
a1573
|
| 1574 |
+
a1574
|
| 1575 |
+
a1575
|
| 1576 |
+
a1576
|
| 1577 |
+
a1577
|
| 1578 |
+
a1578
|
| 1579 |
+
a1579
|
| 1580 |
+
a1580
|
| 1581 |
+
a1581
|
| 1582 |
+
a1582
|
| 1583 |
+
a1583
|
| 1584 |
+
a1584
|
| 1585 |
+
a1585
|
| 1586 |
+
a1586
|
| 1587 |
+
a1587
|
| 1588 |
+
a1588
|
| 1589 |
+
a1589
|
| 1590 |
+
a1590
|
| 1591 |
+
a1591
|
| 1592 |
+
a1592
|
| 1593 |
+
a1593
|
| 1594 |
+
a1594
|
| 1595 |
+
a1595
|
| 1596 |
+
a1596
|
| 1597 |
+
a1597
|
| 1598 |
+
a1598
|
| 1599 |
+
a1599
|
| 1600 |
+
a1600
|
| 1601 |
+
a1601
|
| 1602 |
+
a1602
|
| 1603 |
+
a1603
|
| 1604 |
+
a1604
|
| 1605 |
+
a1605
|
| 1606 |
+
a1606
|
| 1607 |
+
a1607
|
| 1608 |
+
a1608
|
| 1609 |
+
a1609
|
| 1610 |
+
a1610
|
| 1611 |
+
a1611
|
| 1612 |
+
a1612
|
| 1613 |
+
a1613
|
| 1614 |
+
a1614
|
| 1615 |
+
a1615
|
| 1616 |
+
a1616
|
| 1617 |
+
a1617
|
| 1618 |
+
a1618
|
| 1619 |
+
a1619
|
| 1620 |
+
a1620
|
| 1621 |
+
a1621
|
| 1622 |
+
a1622
|
| 1623 |
+
a1623
|
| 1624 |
+
a1624
|
| 1625 |
+
a1625
|
| 1626 |
+
a1626
|
| 1627 |
+
a1627
|
| 1628 |
+
a1628
|
| 1629 |
+
a1629
|
| 1630 |
+
a1630
|
| 1631 |
+
a1631
|
| 1632 |
+
a1632
|
| 1633 |
+
a1633
|
| 1634 |
+
a1634
|
| 1635 |
+
a1635
|
| 1636 |
+
a1636
|
| 1637 |
+
a1637
|
| 1638 |
+
a1638
|
| 1639 |
+
a1639
|
| 1640 |
+
a1640
|
| 1641 |
+
a1641
|
| 1642 |
+
a1642
|
| 1643 |
+
a1643
|
| 1644 |
+
a1644
|
| 1645 |
+
a1645
|
| 1646 |
+
a1646
|
| 1647 |
+
a1647
|
| 1648 |
+
a1648
|
| 1649 |
+
a1649
|
| 1650 |
+
a1650
|
| 1651 |
+
a1651
|
| 1652 |
+
a1652
|
| 1653 |
+
a1653
|
| 1654 |
+
a1654
|
| 1655 |
+
a1655
|
| 1656 |
+
a1656
|
| 1657 |
+
a1657
|
| 1658 |
+
a1658
|
| 1659 |
+
a1659
|
| 1660 |
+
a1660
|
| 1661 |
+
a1661
|
| 1662 |
+
a1662
|
| 1663 |
+
a1663
|
| 1664 |
+
a1664
|
| 1665 |
+
a1665
|
| 1666 |
+
a1666
|
| 1667 |
+
a1667
|
| 1668 |
+
a1668
|
| 1669 |
+
a1669
|
| 1670 |
+
a1670
|
| 1671 |
+
a1671
|
| 1672 |
+
a1672
|
| 1673 |
+
a1673
|
| 1674 |
+
a1674
|
| 1675 |
+
a1675
|
| 1676 |
+
a1676
|
| 1677 |
+
a1677
|
| 1678 |
+
a1678
|
| 1679 |
+
a1679
|
| 1680 |
+
a1680
|
| 1681 |
+
a1681
|
| 1682 |
+
a1682
|
| 1683 |
+
a1683
|
| 1684 |
+
a1684
|
| 1685 |
+
a1685
|
| 1686 |
+
a1686
|
| 1687 |
+
a1687
|
| 1688 |
+
a1688
|
| 1689 |
+
a1689
|
| 1690 |
+
a1690
|
| 1691 |
+
a1691
|
| 1692 |
+
a1692
|
| 1693 |
+
a1693
|
| 1694 |
+
a1694
|
| 1695 |
+
a1695
|
| 1696 |
+
a1696
|
| 1697 |
+
a1697
|
| 1698 |
+
a1698
|
| 1699 |
+
a1699
|
| 1700 |
+
a1700
|
| 1701 |
+
a1701
|
| 1702 |
+
a1702
|
| 1703 |
+
a1703
|
| 1704 |
+
a1704
|
| 1705 |
+
a1705
|
| 1706 |
+
a1706
|
| 1707 |
+
a1707
|
| 1708 |
+
a1708
|
| 1709 |
+
a1709
|
| 1710 |
+
a1710
|
| 1711 |
+
a1711
|
| 1712 |
+
a1712
|
| 1713 |
+
a1713
|
| 1714 |
+
a1714
|
| 1715 |
+
a1715
|
| 1716 |
+
a1716
|
| 1717 |
+
a1717
|
| 1718 |
+
a1718
|
| 1719 |
+
a1719
|
| 1720 |
+
a1720
|
| 1721 |
+
a1721
|
| 1722 |
+
a1722
|
| 1723 |
+
a1723
|
| 1724 |
+
a1724
|
| 1725 |
+
a1725
|
| 1726 |
+
a1726
|
| 1727 |
+
a1727
|
| 1728 |
+
a1728
|
| 1729 |
+
a1729
|
| 1730 |
+
a1730
|
| 1731 |
+
a1731
|
| 1732 |
+
a1732
|
| 1733 |
+
a1733
|
| 1734 |
+
a1734
|
| 1735 |
+
a1735
|
| 1736 |
+
a1736
|
| 1737 |
+
a1737
|
| 1738 |
+
a1738
|
| 1739 |
+
a1739
|
| 1740 |
+
a1740
|
| 1741 |
+
a1741
|
| 1742 |
+
a1742
|
| 1743 |
+
a1743
|
| 1744 |
+
a1744
|
| 1745 |
+
a1745
|
| 1746 |
+
a1746
|
| 1747 |
+
a1747
|
| 1748 |
+
a1748
|
| 1749 |
+
a1749
|
| 1750 |
+
a1750
|
| 1751 |
+
a1751
|
| 1752 |
+
a1752
|
| 1753 |
+
a1753
|
| 1754 |
+
a1754
|
| 1755 |
+
a1755
|
| 1756 |
+
a1756
|
| 1757 |
+
a1757
|
| 1758 |
+
a1758
|
| 1759 |
+
a1759
|
| 1760 |
+
a1760
|
| 1761 |
+
a1761
|
| 1762 |
+
a1762
|
| 1763 |
+
a1763
|
| 1764 |
+
a1764
|
| 1765 |
+
a1765
|
| 1766 |
+
a1766
|
| 1767 |
+
a1767
|
| 1768 |
+
a1768
|
| 1769 |
+
a1769
|
| 1770 |
+
a1770
|
| 1771 |
+
a1771
|
| 1772 |
+
a1772
|
| 1773 |
+
a1773
|
| 1774 |
+
a1774
|
| 1775 |
+
a1775
|
| 1776 |
+
a1776
|
| 1777 |
+
a1777
|
| 1778 |
+
a1778
|
| 1779 |
+
a1779
|
| 1780 |
+
a1780
|
| 1781 |
+
a1781
|
| 1782 |
+
a1782
|
| 1783 |
+
a1783
|
| 1784 |
+
a1784
|
| 1785 |
+
a1785
|
| 1786 |
+
a1786
|
| 1787 |
+
a1787
|
| 1788 |
+
a1788
|
| 1789 |
+
a1789
|
| 1790 |
+
a1790
|
| 1791 |
+
a1791
|
| 1792 |
+
a1792
|
| 1793 |
+
a1793
|
| 1794 |
+
a1794
|
| 1795 |
+
a1795
|
| 1796 |
+
a1796
|
| 1797 |
+
a1797
|
| 1798 |
+
a1798
|
| 1799 |
+
a1799
|
| 1800 |
+
a1800
|
| 1801 |
+
a1801
|
| 1802 |
+
a1802
|
| 1803 |
+
a1803
|
| 1804 |
+
a1804
|
| 1805 |
+
a1805
|
| 1806 |
+
a1806
|
| 1807 |
+
a1807
|
| 1808 |
+
a1808
|
| 1809 |
+
a1809
|
| 1810 |
+
a1810
|
| 1811 |
+
a1811
|
| 1812 |
+
a1812
|
| 1813 |
+
a1813
|
| 1814 |
+
a1814
|
| 1815 |
+
a1815
|
| 1816 |
+
a1816
|
| 1817 |
+
a1817
|
| 1818 |
+
a1818
|
| 1819 |
+
a1819
|
| 1820 |
+
a1820
|
| 1821 |
+
a1821
|
| 1822 |
+
a1822
|
| 1823 |
+
a1823
|
| 1824 |
+
a1824
|
| 1825 |
+
a1825
|
| 1826 |
+
a1826
|
| 1827 |
+
a1827
|
| 1828 |
+
a1828
|
| 1829 |
+
a1829
|
| 1830 |
+
a1830
|
| 1831 |
+
a1831
|
| 1832 |
+
a1832
|
| 1833 |
+
a1833
|
| 1834 |
+
a1834
|
| 1835 |
+
a1835
|
| 1836 |
+
a1836
|
| 1837 |
+
a1837
|
| 1838 |
+
a1838
|
| 1839 |
+
a1839
|
| 1840 |
+
a1840
|
| 1841 |
+
a1841
|
| 1842 |
+
a1842
|
| 1843 |
+
a1843
|
| 1844 |
+
a1844
|
| 1845 |
+
a1845
|
| 1846 |
+
a1846
|
| 1847 |
+
a1847
|
| 1848 |
+
a1848
|
| 1849 |
+
a1849
|
| 1850 |
+
a1850
|
| 1851 |
+
a1851
|
| 1852 |
+
a1852
|
| 1853 |
+
a1853
|
| 1854 |
+
a1854
|
| 1855 |
+
a1855
|
| 1856 |
+
a1856
|
| 1857 |
+
a1857
|
| 1858 |
+
a1858
|
| 1859 |
+
a1859
|
| 1860 |
+
a1860
|
| 1861 |
+
a1861
|
| 1862 |
+
a1862
|
| 1863 |
+
a1863
|
| 1864 |
+
a1864
|
| 1865 |
+
a1865
|
| 1866 |
+
a1866
|
| 1867 |
+
a1867
|
| 1868 |
+
a1868
|
| 1869 |
+
a1869
|
| 1870 |
+
a1870
|
| 1871 |
+
a1871
|
| 1872 |
+
a1872
|
| 1873 |
+
a1873
|
| 1874 |
+
a1874
|
| 1875 |
+
a1875
|
| 1876 |
+
a1876
|
| 1877 |
+
a1877
|
| 1878 |
+
a1878
|
| 1879 |
+
a1879
|
| 1880 |
+
a1880
|
| 1881 |
+
a1881
|
| 1882 |
+
a1882
|
| 1883 |
+
a1883
|
| 1884 |
+
a1884
|
| 1885 |
+
a1885
|
| 1886 |
+
a1886
|
| 1887 |
+
a1887
|
| 1888 |
+
a1888
|
| 1889 |
+
a1889
|
| 1890 |
+
a1890
|
| 1891 |
+
a1891
|
| 1892 |
+
a1892
|
| 1893 |
+
a1893
|
| 1894 |
+
a1894
|
| 1895 |
+
a1895
|
| 1896 |
+
a1896
|
| 1897 |
+
a1897
|
| 1898 |
+
a1898
|
| 1899 |
+
a1899
|
| 1900 |
+
a1900
|
| 1901 |
+
a1901
|
| 1902 |
+
a1902
|
| 1903 |
+
a1903
|
| 1904 |
+
a1904
|
| 1905 |
+
a1905
|
| 1906 |
+
a1906
|
| 1907 |
+
a1907
|
| 1908 |
+
a1908
|
| 1909 |
+
a1909
|
| 1910 |
+
a1910
|
| 1911 |
+
a1911
|
| 1912 |
+
a1912
|
| 1913 |
+
a1913
|
| 1914 |
+
a1914
|
| 1915 |
+
a1915
|
| 1916 |
+
a1916
|
| 1917 |
+
a1917
|
| 1918 |
+
a1918
|
| 1919 |
+
a1919
|
| 1920 |
+
a1920
|
| 1921 |
+
a1921
|
| 1922 |
+
a1922
|
| 1923 |
+
a1923
|
| 1924 |
+
a1924
|
| 1925 |
+
a1925
|
| 1926 |
+
a1926
|
| 1927 |
+
a1927
|
| 1928 |
+
a1928
|
| 1929 |
+
a1929
|
| 1930 |
+
a1930
|
| 1931 |
+
a1931
|
| 1932 |
+
a1932
|
| 1933 |
+
a1933
|
| 1934 |
+
a1934
|
| 1935 |
+
a1935
|
| 1936 |
+
a1936
|
| 1937 |
+
a1937
|
| 1938 |
+
a1938
|
| 1939 |
+
a1939
|
| 1940 |
+
a1940
|
| 1941 |
+
a1941
|
| 1942 |
+
a1942
|
| 1943 |
+
a1943
|
| 1944 |
+
a1944
|
| 1945 |
+
a1945
|
| 1946 |
+
a1946
|
| 1947 |
+
a1947
|
| 1948 |
+
a1948
|
| 1949 |
+
a1949
|
| 1950 |
+
a1950
|
| 1951 |
+
a1951
|
| 1952 |
+
a1952
|
| 1953 |
+
a1953
|
| 1954 |
+
a1954
|
| 1955 |
+
a1955
|
| 1956 |
+
a1956
|
| 1957 |
+
a1957
|
| 1958 |
+
a1958
|
| 1959 |
+
a1959
|
| 1960 |
+
a1960
|
| 1961 |
+
a1961
|
| 1962 |
+
a1962
|
| 1963 |
+
a1963
|
| 1964 |
+
a1964
|
| 1965 |
+
a1965
|
| 1966 |
+
a1966
|
| 1967 |
+
a1967
|
| 1968 |
+
a1968
|
| 1969 |
+
a1969
|
| 1970 |
+
a1970
|
| 1971 |
+
a1971
|
| 1972 |
+
a1972
|
| 1973 |
+
a1973
|
| 1974 |
+
a1974
|
| 1975 |
+
a1975
|
| 1976 |
+
a1976
|
| 1977 |
+
a1977
|
| 1978 |
+
a1978
|
| 1979 |
+
a1979
|
| 1980 |
+
a1980
|
| 1981 |
+
a1981
|
| 1982 |
+
a1982
|
| 1983 |
+
a1983
|
| 1984 |
+
a1984
|
| 1985 |
+
a1985
|
| 1986 |
+
a1986
|
| 1987 |
+
a1987
|
| 1988 |
+
a1988
|
| 1989 |
+
a1989
|
| 1990 |
+
a1990
|
| 1991 |
+
a1991
|
| 1992 |
+
a1992
|
| 1993 |
+
a1993
|
| 1994 |
+
a1994
|
| 1995 |
+
a1995
|
| 1996 |
+
a1996
|
| 1997 |
+
a1997
|
| 1998 |
+
a1998
|
| 1999 |
+
a1999
|
| 2000 |
+
a2000
|
| 2001 |
+
a2001
|
| 2002 |
+
a2002
|
| 2003 |
+
a2003
|
| 2004 |
+
a2004
|
| 2005 |
+
a2005
|
| 2006 |
+
a2006
|
| 2007 |
+
a2007
|
| 2008 |
+
a2008
|
| 2009 |
+
a2009
|
| 2010 |
+
a2010
|
| 2011 |
+
a2011
|
| 2012 |
+
a2012
|
| 2013 |
+
a2013
|
| 2014 |
+
a2014
|
| 2015 |
+
a2015
|
| 2016 |
+
a2016
|
| 2017 |
+
a2017
|
| 2018 |
+
a2018
|
| 2019 |
+
a2019
|
| 2020 |
+
a2020
|
| 2021 |
+
a2021
|
| 2022 |
+
a2022
|
| 2023 |
+
a2023
|
| 2024 |
+
a2024
|
| 2025 |
+
a2025
|
| 2026 |
+
a2026
|
| 2027 |
+
a2027
|
| 2028 |
+
a2028
|
| 2029 |
+
a2029
|
| 2030 |
+
a2030
|
| 2031 |
+
a2031
|
| 2032 |
+
a2032
|
| 2033 |
+
a2033
|
| 2034 |
+
a2034
|
| 2035 |
+
a2035
|
| 2036 |
+
a2036
|
| 2037 |
+
a2037
|
| 2038 |
+
a2038
|
| 2039 |
+
a2039
|
| 2040 |
+
a2040
|
| 2041 |
+
a2041
|
| 2042 |
+
a2042
|
| 2043 |
+
a2043
|
| 2044 |
+
a2044
|
| 2045 |
+
a2045
|
| 2046 |
+
a2046
|
| 2047 |
+
a2047
|
| 2048 |
+
a2048
|
| 2049 |
+
a2049
|
| 2050 |
+
a2050
|
| 2051 |
+
a2051
|
| 2052 |
+
a2052
|
| 2053 |
+
a2053
|
| 2054 |
+
a2054
|
| 2055 |
+
a2055
|
| 2056 |
+
a2056
|
| 2057 |
+
a2057
|
| 2058 |
+
a2058
|
| 2059 |
+
a2059
|
| 2060 |
+
a2060
|
| 2061 |
+
a2061
|
| 2062 |
+
a2062
|
| 2063 |
+
a2063
|
| 2064 |
+
a2064
|
| 2065 |
+
a2065
|
| 2066 |
+
a2066
|
| 2067 |
+
a2067
|
| 2068 |
+
a2068
|
| 2069 |
+
a2069
|
| 2070 |
+
a2070
|
| 2071 |
+
a2071
|
| 2072 |
+
a2072
|
| 2073 |
+
a2073
|
| 2074 |
+
a2074
|
| 2075 |
+
a2075
|
| 2076 |
+
a2076
|
| 2077 |
+
a2077
|
| 2078 |
+
a2078
|
| 2079 |
+
a2079
|
| 2080 |
+
a2080
|
| 2081 |
+
a2081
|
| 2082 |
+
a2082
|
| 2083 |
+
a2083
|
| 2084 |
+
a2084
|
| 2085 |
+
a2085
|
| 2086 |
+
a2086
|
| 2087 |
+
a2087
|
| 2088 |
+
a2088
|
| 2089 |
+
a2089
|
| 2090 |
+
a2090
|
| 2091 |
+
a2091
|
| 2092 |
+
a2092
|
| 2093 |
+
a2093
|
| 2094 |
+
a2094
|
| 2095 |
+
a2095
|
| 2096 |
+
a2096
|
| 2097 |
+
a2097
|
| 2098 |
+
a2098
|
| 2099 |
+
a2099
|
| 2100 |
+
a2100
|
| 2101 |
+
a2101
|
| 2102 |
+
a2102
|
| 2103 |
+
a2103
|
| 2104 |
+
a2104
|
| 2105 |
+
a2105
|
| 2106 |
+
a2106
|
| 2107 |
+
a2107
|
| 2108 |
+
a2108
|
| 2109 |
+
a2109
|
| 2110 |
+
a2110
|
| 2111 |
+
a2111
|
| 2112 |
+
a2112
|
| 2113 |
+
a2113
|
| 2114 |
+
a2114
|
| 2115 |
+
a2115
|
| 2116 |
+
a2116
|
| 2117 |
+
a2117
|
| 2118 |
+
a2118
|
| 2119 |
+
a2119
|
| 2120 |
+
a2120
|
| 2121 |
+
a2121
|
| 2122 |
+
a2122
|
| 2123 |
+
a2123
|
| 2124 |
+
a2124
|
| 2125 |
+
a2125
|
| 2126 |
+
a2126
|
| 2127 |
+
a2127
|
| 2128 |
+
a2128
|
| 2129 |
+
a2129
|
| 2130 |
+
a2130
|
| 2131 |
+
a2131
|
| 2132 |
+
a2132
|
| 2133 |
+
a2133
|
| 2134 |
+
a2134
|
| 2135 |
+
a2135
|
| 2136 |
+
a2136
|
| 2137 |
+
a2137
|
| 2138 |
+
a2138
|
| 2139 |
+
a2139
|
| 2140 |
+
a2140
|
| 2141 |
+
a2141
|
| 2142 |
+
a2142
|
| 2143 |
+
a2143
|
| 2144 |
+
a2144
|
| 2145 |
+
a2145
|
| 2146 |
+
a2146
|
| 2147 |
+
a2147
|
| 2148 |
+
a2148
|
| 2149 |
+
a2149
|
| 2150 |
+
a2150
|
| 2151 |
+
a2151
|
| 2152 |
+
a2152
|
| 2153 |
+
a2153
|
| 2154 |
+
a2154
|
| 2155 |
+
a2155
|
| 2156 |
+
a2156
|
| 2157 |
+
a2157
|
| 2158 |
+
a2158
|
| 2159 |
+
a2159
|
| 2160 |
+
a2160
|
| 2161 |
+
a2161
|
| 2162 |
+
a2162
|
| 2163 |
+
a2163
|
| 2164 |
+
a2164
|
| 2165 |
+
a2165
|
| 2166 |
+
a2166
|
| 2167 |
+
a2167
|
| 2168 |
+
a2168
|
| 2169 |
+
a2169
|
| 2170 |
+
a2170
|
| 2171 |
+
a2171
|
| 2172 |
+
a2172
|
| 2173 |
+
a2173
|
| 2174 |
+
a2174
|
| 2175 |
+
a2175
|
| 2176 |
+
a2176
|
| 2177 |
+
a2177
|
| 2178 |
+
a2178
|
| 2179 |
+
a2179
|
| 2180 |
+
a2180
|
| 2181 |
+
a2181
|
| 2182 |
+
a2182
|
| 2183 |
+
a2183
|
| 2184 |
+
a2184
|
| 2185 |
+
a2185
|
| 2186 |
+
a2186
|
| 2187 |
+
a2187
|
| 2188 |
+
a2188
|
| 2189 |
+
a2189
|
| 2190 |
+
a2190
|
| 2191 |
+
a2191
|
| 2192 |
+
a2192
|
| 2193 |
+
a2193
|
| 2194 |
+
a2194
|
| 2195 |
+
a2195
|
| 2196 |
+
a2196
|
| 2197 |
+
a2197
|
| 2198 |
+
a2198
|
| 2199 |
+
a2199
|
| 2200 |
+
a2200
|
| 2201 |
+
a2201
|
| 2202 |
+
a2202
|
| 2203 |
+
a2203
|
| 2204 |
+
a2204
|
| 2205 |
+
a2205
|
| 2206 |
+
a2206
|
| 2207 |
+
a2207
|
| 2208 |
+
a2208
|
| 2209 |
+
a2209
|
| 2210 |
+
a2210
|
| 2211 |
+
a2211
|
| 2212 |
+
a2212
|
| 2213 |
+
a2213
|
| 2214 |
+
a2214
|
| 2215 |
+
a2215
|
| 2216 |
+
a2216
|
| 2217 |
+
a2217
|
| 2218 |
+
a2218
|
| 2219 |
+
a2219
|
| 2220 |
+
a2220
|
| 2221 |
+
a2221
|
| 2222 |
+
a2222
|
| 2223 |
+
a2223
|
| 2224 |
+
a2224
|
| 2225 |
+
a2225
|
| 2226 |
+
a2226
|
| 2227 |
+
a2227
|
| 2228 |
+
a2228
|
| 2229 |
+
a2229
|
| 2230 |
+
a2230
|
| 2231 |
+
a2231
|
| 2232 |
+
a2232
|
| 2233 |
+
a2233
|
| 2234 |
+
a2234
|
| 2235 |
+
a2235
|
| 2236 |
+
a2236
|
| 2237 |
+
a2237
|
| 2238 |
+
a2238
|
| 2239 |
+
a2239
|
| 2240 |
+
a2240
|
| 2241 |
+
a2241
|
| 2242 |
+
a2242
|
| 2243 |
+
a2243
|
| 2244 |
+
a2244
|
| 2245 |
+
a2245
|
| 2246 |
+
a2246
|
| 2247 |
+
a2247
|
| 2248 |
+
a2248
|
| 2249 |
+
a2249
|
| 2250 |
+
a2250
|
| 2251 |
+
a2251
|
| 2252 |
+
a2252
|
| 2253 |
+
a2253
|
| 2254 |
+
a2254
|
| 2255 |
+
a2255
|
| 2256 |
+
a2256
|
| 2257 |
+
a2257
|
| 2258 |
+
a2258
|
| 2259 |
+
a2259
|
| 2260 |
+
a2260
|
| 2261 |
+
a2261
|
| 2262 |
+
a2262
|
| 2263 |
+
a2263
|
| 2264 |
+
a2264
|
| 2265 |
+
a2265
|
| 2266 |
+
a2266
|
| 2267 |
+
a2267
|
| 2268 |
+
a2268
|
| 2269 |
+
a2269
|
| 2270 |
+
a2270
|
| 2271 |
+
a2271
|
| 2272 |
+
a2272
|
| 2273 |
+
a2273
|
| 2274 |
+
a2274
|
| 2275 |
+
a2275
|
| 2276 |
+
a2276
|
| 2277 |
+
a2277
|
| 2278 |
+
a2278
|
| 2279 |
+
a2279
|
| 2280 |
+
a2280
|
| 2281 |
+
a2281
|
| 2282 |
+
a2282
|
| 2283 |
+
a2283
|
| 2284 |
+
a2284
|
| 2285 |
+
a2285
|
| 2286 |
+
a2286
|
| 2287 |
+
a2287
|
| 2288 |
+
a2288
|
| 2289 |
+
a2289
|
| 2290 |
+
a2290
|
| 2291 |
+
a2291
|
| 2292 |
+
a2292
|
| 2293 |
+
a2293
|
| 2294 |
+
a2294
|
| 2295 |
+
a2295
|
| 2296 |
+
a2296
|
| 2297 |
+
a2297
|
| 2298 |
+
a2298
|
| 2299 |
+
a2299
|
| 2300 |
+
a2300
|
| 2301 |
+
a2301
|
| 2302 |
+
a2302
|
| 2303 |
+
a2303
|
| 2304 |
+
a2304
|
| 2305 |
+
a2305
|
| 2306 |
+
a2306
|
| 2307 |
+
a2307
|
| 2308 |
+
a2308
|
| 2309 |
+
a2309
|
| 2310 |
+
a2310
|
| 2311 |
+
a2311
|
| 2312 |
+
a2312
|
| 2313 |
+
a2313
|
| 2314 |
+
a2314
|
| 2315 |
+
a2315
|
| 2316 |
+
a2316
|
| 2317 |
+
a2317
|
| 2318 |
+
a2318
|
| 2319 |
+
a2319
|
| 2320 |
+
a2320
|
| 2321 |
+
a2321
|
| 2322 |
+
a2322
|
| 2323 |
+
a2323
|
| 2324 |
+
a2324
|
| 2325 |
+
a2325
|
| 2326 |
+
a2326
|
| 2327 |
+
a2327
|
| 2328 |
+
a2328
|
| 2329 |
+
a2329
|
| 2330 |
+
a2330
|
| 2331 |
+
a2331
|
| 2332 |
+
a2332
|
| 2333 |
+
a2333
|
| 2334 |
+
a2334
|
| 2335 |
+
a2335
|
| 2336 |
+
a2336
|
| 2337 |
+
a2337
|
| 2338 |
+
a2338
|
| 2339 |
+
a2339
|
| 2340 |
+
a2340
|
| 2341 |
+
a2341
|
| 2342 |
+
a2342
|
| 2343 |
+
a2343
|
| 2344 |
+
a2344
|
| 2345 |
+
a2345
|
| 2346 |
+
a2346
|
| 2347 |
+
a2347
|
| 2348 |
+
a2348
|
| 2349 |
+
a2349
|
| 2350 |
+
a2350
|
| 2351 |
+
a2351
|
| 2352 |
+
a2352
|
| 2353 |
+
a2353
|
| 2354 |
+
a2354
|
| 2355 |
+
a2355
|
| 2356 |
+
a2356
|
| 2357 |
+
a2357
|
| 2358 |
+
a2358
|
| 2359 |
+
a2359
|
| 2360 |
+
a2360
|
| 2361 |
+
a2361
|
| 2362 |
+
a2362
|
| 2363 |
+
a2363
|
| 2364 |
+
a2364
|
| 2365 |
+
a2365
|
| 2366 |
+
a2366
|
| 2367 |
+
a2367
|
| 2368 |
+
a2368
|
| 2369 |
+
a2369
|
| 2370 |
+
a2370
|
| 2371 |
+
a2371
|
| 2372 |
+
a2372
|
| 2373 |
+
a2373
|
| 2374 |
+
a2374
|
| 2375 |
+
a2375
|
| 2376 |
+
a2376
|
| 2377 |
+
a2377
|
| 2378 |
+
a2378
|
| 2379 |
+
a2379
|
| 2380 |
+
a2380
|
| 2381 |
+
a2381
|
| 2382 |
+
a2382
|
| 2383 |
+
a2383
|
| 2384 |
+
a2384
|
| 2385 |
+
a2385
|
| 2386 |
+
a2386
|
| 2387 |
+
a2387
|
| 2388 |
+
a2388
|
| 2389 |
+
a2389
|
| 2390 |
+
a2390
|
| 2391 |
+
a2391
|
| 2392 |
+
a2392
|
| 2393 |
+
a2393
|
| 2394 |
+
a2394
|
| 2395 |
+
a2395
|
| 2396 |
+
a2396
|
| 2397 |
+
a2397
|
| 2398 |
+
a2398
|
| 2399 |
+
a2399
|
| 2400 |
+
a2400
|
| 2401 |
+
a2401
|
| 2402 |
+
a2402
|
| 2403 |
+
a2403
|
| 2404 |
+
a2404
|
| 2405 |
+
a2405
|
| 2406 |
+
a2406
|
| 2407 |
+
a2407
|
| 2408 |
+
a2408
|
| 2409 |
+
a2409
|
| 2410 |
+
a2410
|
| 2411 |
+
a2411
|
| 2412 |
+
a2412
|
| 2413 |
+
a2413
|
| 2414 |
+
a2414
|
| 2415 |
+
a2415
|
| 2416 |
+
a2416
|
| 2417 |
+
a2417
|
| 2418 |
+
a2418
|
| 2419 |
+
a2419
|
| 2420 |
+
a2420
|
| 2421 |
+
a2421
|
| 2422 |
+
a2422
|
| 2423 |
+
a2423
|
| 2424 |
+
a2424
|
| 2425 |
+
a2425
|
| 2426 |
+
a2426
|
| 2427 |
+
a2427
|
| 2428 |
+
a2428
|
| 2429 |
+
a2429
|
| 2430 |
+
a2430
|
| 2431 |
+
a2431
|
| 2432 |
+
a2432
|
| 2433 |
+
a2433
|
| 2434 |
+
a2434
|
| 2435 |
+
a2435
|
| 2436 |
+
a2436
|
| 2437 |
+
a2437
|
| 2438 |
+
a2438
|
| 2439 |
+
a2439
|
| 2440 |
+
a2440
|
| 2441 |
+
a2441
|
| 2442 |
+
a2442
|
| 2443 |
+
a2443
|
| 2444 |
+
a2444
|
| 2445 |
+
a2445
|
| 2446 |
+
a2446
|
| 2447 |
+
a2447
|
| 2448 |
+
a2448
|
| 2449 |
+
a2449
|
| 2450 |
+
a2450
|
| 2451 |
+
a2451
|
| 2452 |
+
a2452
|
| 2453 |
+
a2453
|
| 2454 |
+
a2454
|
| 2455 |
+
a2455
|
| 2456 |
+
a2456
|
| 2457 |
+
a2457
|
| 2458 |
+
a2458
|
| 2459 |
+
a2459
|
| 2460 |
+
a2460
|
| 2461 |
+
a2461
|
| 2462 |
+
a2462
|
| 2463 |
+
a2463
|
| 2464 |
+
a2464
|
| 2465 |
+
a2465
|
| 2466 |
+
a2466
|
| 2467 |
+
a2467
|
| 2468 |
+
a2468
|
| 2469 |
+
a2469
|
| 2470 |
+
a2470
|
| 2471 |
+
a2471
|
| 2472 |
+
a2472
|
| 2473 |
+
a2473
|
| 2474 |
+
a2474
|
| 2475 |
+
a2475
|
| 2476 |
+
a2476
|
| 2477 |
+
a2477
|
| 2478 |
+
a2478
|
| 2479 |
+
a2479
|
| 2480 |
+
a2480
|
| 2481 |
+
a2481
|
| 2482 |
+
a2482
|
| 2483 |
+
a2483
|
| 2484 |
+
a2484
|
| 2485 |
+
a2485
|
| 2486 |
+
a2486
|
| 2487 |
+
a2487
|
| 2488 |
+
a2488
|
| 2489 |
+
a2489
|
| 2490 |
+
a2490
|
| 2491 |
+
a2491
|
| 2492 |
+
a2492
|
| 2493 |
+
a2493
|
| 2494 |
+
a2494
|
| 2495 |
+
a2495
|
| 2496 |
+
a2496
|
| 2497 |
+
a2497
|
| 2498 |
+
a2498
|
| 2499 |
+
a2499
|
| 2500 |
+
a2500
|
| 2501 |
+
a2501
|
| 2502 |
+
a2502
|
| 2503 |
+
a2503
|
| 2504 |
+
a2504
|
| 2505 |
+
a2505
|
| 2506 |
+
a2506
|
| 2507 |
+
a2507
|
| 2508 |
+
a2508
|
| 2509 |
+
a2509
|
| 2510 |
+
a2510
|
| 2511 |
+
a2511
|
| 2512 |
+
a2512
|
| 2513 |
+
a2513
|
| 2514 |
+
a2514
|
| 2515 |
+
a2515
|
| 2516 |
+
a2516
|
| 2517 |
+
a2517
|
| 2518 |
+
a2518
|
| 2519 |
+
a2519
|
| 2520 |
+
a2520
|
| 2521 |
+
a2521
|
| 2522 |
+
a2522
|
| 2523 |
+
a2523
|
| 2524 |
+
a2524
|
| 2525 |
+
a2525
|
| 2526 |
+
a2526
|
| 2527 |
+
a2527
|
| 2528 |
+
a2528
|
| 2529 |
+
a2529
|
| 2530 |
+
a2530
|
| 2531 |
+
a2531
|
| 2532 |
+
a2532
|
| 2533 |
+
a2533
|
| 2534 |
+
a2534
|
| 2535 |
+
a2535
|
| 2536 |
+
a2536
|
| 2537 |
+
a2537
|
| 2538 |
+
a2538
|
| 2539 |
+
a2539
|
| 2540 |
+
a2540
|
| 2541 |
+
a2541
|
| 2542 |
+
a2542
|
| 2543 |
+
a2543
|
| 2544 |
+
a2544
|
| 2545 |
+
a2545
|
| 2546 |
+
a2546
|
| 2547 |
+
a2547
|
| 2548 |
+
a2548
|
| 2549 |
+
a2549
|
| 2550 |
+
a2550
|
| 2551 |
+
a2551
|
| 2552 |
+
a2552
|
| 2553 |
+
a2553
|
| 2554 |
+
a2554
|
| 2555 |
+
a2555
|
| 2556 |
+
a2556
|
| 2557 |
+
a2557
|
| 2558 |
+
a2558
|
| 2559 |
+
a2559
|
| 2560 |
+
a2560
|
| 2561 |
+
a2561
|
| 2562 |
+
a2562
|
| 2563 |
+
a2563
|
| 2564 |
+
a2564
|
| 2565 |
+
a2565
|
| 2566 |
+
a2566
|
| 2567 |
+
a2567
|
| 2568 |
+
a2568
|
| 2569 |
+
a2569
|
| 2570 |
+
a2570
|
| 2571 |
+
a2571
|
| 2572 |
+
a2572
|
| 2573 |
+
a2573
|
| 2574 |
+
a2574
|
| 2575 |
+
a2575
|
| 2576 |
+
a2576
|
| 2577 |
+
a2577
|
| 2578 |
+
a2578
|
| 2579 |
+
a2579
|
| 2580 |
+
a2580
|
| 2581 |
+
a2581
|
| 2582 |
+
a2582
|
| 2583 |
+
a2583
|
| 2584 |
+
a2584
|
| 2585 |
+
a2585
|
| 2586 |
+
a2586
|
| 2587 |
+
a2587
|
| 2588 |
+
a2588
|
| 2589 |
+
a2589
|
| 2590 |
+
a2590
|
| 2591 |
+
a2591
|
| 2592 |
+
a2592
|
| 2593 |
+
a2593
|
| 2594 |
+
a2594
|
| 2595 |
+
a2595
|
| 2596 |
+
a2596
|
| 2597 |
+
a2597
|
| 2598 |
+
a2598
|
| 2599 |
+
a2599
|
| 2600 |
+
a2600
|
| 2601 |
+
a2601
|
| 2602 |
+
a2602
|
| 2603 |
+
a2603
|
| 2604 |
+
a2604
|
| 2605 |
+
a2605
|
| 2606 |
+
a2606
|
| 2607 |
+
a2607
|
| 2608 |
+
a2608
|
| 2609 |
+
a2609
|
| 2610 |
+
a2610
|
| 2611 |
+
a2611
|
| 2612 |
+
a2612
|
| 2613 |
+
a2613
|
| 2614 |
+
a2614
|
| 2615 |
+
a2615
|
| 2616 |
+
a2616
|
| 2617 |
+
a2617
|
| 2618 |
+
a2618
|
| 2619 |
+
a2619
|
| 2620 |
+
a2620
|
| 2621 |
+
a2621
|
| 2622 |
+
a2622
|
| 2623 |
+
a2623
|
| 2624 |
+
a2624
|
| 2625 |
+
a2625
|
| 2626 |
+
a2626
|
| 2627 |
+
a2627
|
| 2628 |
+
a2628
|
| 2629 |
+
a2629
|
| 2630 |
+
a2630
|
| 2631 |
+
a2631
|
| 2632 |
+
a2632
|
| 2633 |
+
a2633
|
| 2634 |
+
a2634
|
| 2635 |
+
a2635
|
| 2636 |
+
a2636
|
| 2637 |
+
a2637
|
| 2638 |
+
a2638
|
| 2639 |
+
a2639
|
| 2640 |
+
a2640
|
| 2641 |
+
a2641
|
| 2642 |
+
a2642
|
| 2643 |
+
a2643
|
| 2644 |
+
a2644
|
| 2645 |
+
a2645
|
| 2646 |
+
a2646
|
| 2647 |
+
a2647
|
| 2648 |
+
a2648
|
| 2649 |
+
a2649
|
| 2650 |
+
a2650
|
| 2651 |
+
a2651
|
| 2652 |
+
a2652
|
| 2653 |
+
a2653
|
| 2654 |
+
a2654
|
| 2655 |
+
a2655
|
| 2656 |
+
a2656
|
| 2657 |
+
a2657
|
| 2658 |
+
a2658
|
| 2659 |
+
a2659
|
| 2660 |
+
a2660
|
| 2661 |
+
a2661
|
| 2662 |
+
a2662
|
| 2663 |
+
a2663
|
| 2664 |
+
a2664
|
| 2665 |
+
a2665
|
| 2666 |
+
a2666
|
| 2667 |
+
a2667
|
| 2668 |
+
a2668
|
| 2669 |
+
a2669
|
| 2670 |
+
a2670
|
| 2671 |
+
a2671
|
| 2672 |
+
a2672
|
| 2673 |
+
a2673
|
| 2674 |
+
a2674
|
| 2675 |
+
a2675
|
| 2676 |
+
a2676
|
| 2677 |
+
a2677
|
| 2678 |
+
a2678
|
| 2679 |
+
a2679
|
| 2680 |
+
a2680
|
| 2681 |
+
a2681
|
| 2682 |
+
a2682
|
| 2683 |
+
a2683
|
| 2684 |
+
a2684
|
| 2685 |
+
a2685
|
| 2686 |
+
a2686
|
| 2687 |
+
a2687
|
| 2688 |
+
a2688
|
| 2689 |
+
a2689
|
| 2690 |
+
a2690
|
| 2691 |
+
a2691
|
| 2692 |
+
a2692
|
| 2693 |
+
a2693
|
| 2694 |
+
a2694
|
| 2695 |
+
a2695
|
| 2696 |
+
a2696
|
| 2697 |
+
a2697
|
| 2698 |
+
a2698
|
| 2699 |
+
a2699
|
| 2700 |
+
a2700
|
| 2701 |
+
a2701
|
| 2702 |
+
a2702
|
| 2703 |
+
a2703
|
| 2704 |
+
a2704
|
| 2705 |
+
a2705
|
| 2706 |
+
a2706
|
| 2707 |
+
a2707
|
| 2708 |
+
a2708
|
| 2709 |
+
a2709
|
| 2710 |
+
a2710
|
| 2711 |
+
a2711
|
| 2712 |
+
a2712
|
| 2713 |
+
a2713
|
| 2714 |
+
a2714
|
| 2715 |
+
a2715
|
| 2716 |
+
a2716
|
| 2717 |
+
a2717
|
| 2718 |
+
a2718
|
| 2719 |
+
a2719
|
| 2720 |
+
a2720
|
| 2721 |
+
a2721
|
| 2722 |
+
a2722
|
| 2723 |
+
a2723
|
| 2724 |
+
a2724
|
| 2725 |
+
a2725
|
| 2726 |
+
a2726
|
| 2727 |
+
a2727
|
| 2728 |
+
a2728
|
| 2729 |
+
a2729
|
| 2730 |
+
a2730
|
| 2731 |
+
a2731
|
| 2732 |
+
a2732
|
| 2733 |
+
a2733
|
| 2734 |
+
a2734
|
| 2735 |
+
a2735
|
| 2736 |
+
a2736
|
| 2737 |
+
a2737
|
| 2738 |
+
a2738
|
| 2739 |
+
a2739
|
| 2740 |
+
a2740
|
| 2741 |
+
a2741
|
| 2742 |
+
a2742
|
| 2743 |
+
a2743
|
| 2744 |
+
a2744
|
| 2745 |
+
a2745
|
| 2746 |
+
a2746
|
| 2747 |
+
a2747
|
| 2748 |
+
a2748
|
| 2749 |
+
a2749
|
| 2750 |
+
a2750
|
| 2751 |
+
a2751
|
| 2752 |
+
a2752
|
| 2753 |
+
a2753
|
| 2754 |
+
a2754
|
| 2755 |
+
a2755
|
| 2756 |
+
a2756
|
| 2757 |
+
a2757
|
| 2758 |
+
a2758
|
| 2759 |
+
a2759
|
| 2760 |
+
a2760
|
| 2761 |
+
a2761
|
| 2762 |
+
a2762
|
| 2763 |
+
a2763
|
| 2764 |
+
a2764
|
| 2765 |
+
a2765
|
| 2766 |
+
a2766
|
| 2767 |
+
a2767
|
| 2768 |
+
a2768
|
| 2769 |
+
a2769
|
| 2770 |
+
a2770
|
| 2771 |
+
a2771
|
| 2772 |
+
a2772
|
| 2773 |
+
a2773
|
| 2774 |
+
a2774
|
| 2775 |
+
a2775
|
| 2776 |
+
a2776
|
| 2777 |
+
a2777
|
| 2778 |
+
a2778
|
| 2779 |
+
a2779
|
| 2780 |
+
a2780
|
| 2781 |
+
a2781
|
| 2782 |
+
a2782
|
| 2783 |
+
a2783
|
| 2784 |
+
a2784
|
| 2785 |
+
a2785
|
| 2786 |
+
a2786
|
| 2787 |
+
a2787
|
| 2788 |
+
a2788
|
| 2789 |
+
a2789
|
| 2790 |
+
a2790
|
| 2791 |
+
a2791
|
| 2792 |
+
a2792
|
| 2793 |
+
a2793
|
| 2794 |
+
a2794
|
| 2795 |
+
a2795
|
| 2796 |
+
a2796
|
| 2797 |
+
a2797
|
| 2798 |
+
a2798
|
| 2799 |
+
a2799
|
| 2800 |
+
a2800
|
| 2801 |
+
a2801
|
| 2802 |
+
a2802
|
| 2803 |
+
a2803
|
| 2804 |
+
a2804
|
| 2805 |
+
a2805
|
| 2806 |
+
a2806
|
| 2807 |
+
a2807
|
| 2808 |
+
a2808
|
| 2809 |
+
a2809
|
| 2810 |
+
a2810
|
| 2811 |
+
a2811
|
| 2812 |
+
a2812
|
| 2813 |
+
a2813
|
| 2814 |
+
a2814
|
| 2815 |
+
a2815
|
| 2816 |
+
a2816
|
| 2817 |
+
a2817
|
| 2818 |
+
a2818
|
| 2819 |
+
a2819
|
| 2820 |
+
a2820
|
| 2821 |
+
a2821
|
| 2822 |
+
a2822
|
| 2823 |
+
a2823
|
| 2824 |
+
a2824
|
| 2825 |
+
a2825
|
| 2826 |
+
a2826
|
| 2827 |
+
a2827
|
| 2828 |
+
a2828
|
| 2829 |
+
a2829
|
| 2830 |
+
a2830
|
| 2831 |
+
a2831
|
| 2832 |
+
a2832
|
| 2833 |
+
a2833
|
| 2834 |
+
a2834
|
| 2835 |
+
a2835
|
| 2836 |
+
a2836
|
| 2837 |
+
a2837
|
| 2838 |
+
a2838
|
| 2839 |
+
a2839
|
| 2840 |
+
a2840
|
| 2841 |
+
a2841
|
| 2842 |
+
a2842
|
| 2843 |
+
a2843
|
| 2844 |
+
a2844
|
| 2845 |
+
a2845
|
| 2846 |
+
a2846
|
| 2847 |
+
a2847
|
| 2848 |
+
a2848
|
| 2849 |
+
a2849
|
| 2850 |
+
a2850
|
| 2851 |
+
a2851
|
| 2852 |
+
a2852
|
| 2853 |
+
a2853
|
| 2854 |
+
a2854
|
| 2855 |
+
a2855
|
| 2856 |
+
a2856
|
| 2857 |
+
a2857
|
| 2858 |
+
a2858
|
| 2859 |
+
a2859
|
| 2860 |
+
a2860
|
| 2861 |
+
a2861
|
| 2862 |
+
a2862
|
| 2863 |
+
a2863
|
| 2864 |
+
a2864
|
| 2865 |
+
a2865
|
| 2866 |
+
a2866
|
| 2867 |
+
a2867
|
| 2868 |
+
a2868
|
| 2869 |
+
a2869
|
| 2870 |
+
a2870
|
| 2871 |
+
a2871
|
| 2872 |
+
a2872
|
| 2873 |
+
a2873
|
| 2874 |
+
a2874
|
| 2875 |
+
a2875
|
| 2876 |
+
a2876
|
| 2877 |
+
a2877
|
| 2878 |
+
a2878
|
| 2879 |
+
a2879
|
| 2880 |
+
a2880
|
| 2881 |
+
a2881
|
| 2882 |
+
a2882
|
| 2883 |
+
a2883
|
| 2884 |
+
a2884
|
| 2885 |
+
a2885
|
| 2886 |
+
a2886
|
| 2887 |
+
a2887
|
| 2888 |
+
a2888
|
| 2889 |
+
a2889
|
| 2890 |
+
a2890
|
| 2891 |
+
a2891
|
| 2892 |
+
a2892
|
| 2893 |
+
a2893
|
| 2894 |
+
a2894
|
| 2895 |
+
a2895
|
| 2896 |
+
a2896
|
| 2897 |
+
a2897
|
| 2898 |
+
a2898
|
| 2899 |
+
a2899
|
| 2900 |
+
a2900
|
| 2901 |
+
a2901
|
| 2902 |
+
a2902
|
| 2903 |
+
a2903
|
| 2904 |
+
a2904
|
| 2905 |
+
a2905
|
| 2906 |
+
a2906
|
| 2907 |
+
a2907
|
| 2908 |
+
a2908
|
| 2909 |
+
a2909
|
| 2910 |
+
a2910
|
| 2911 |
+
a2911
|
| 2912 |
+
a2912
|
| 2913 |
+
a2913
|
| 2914 |
+
a2914
|
| 2915 |
+
a2915
|
| 2916 |
+
a2916
|
| 2917 |
+
a2917
|
| 2918 |
+
a2918
|
| 2919 |
+
a2919
|
| 2920 |
+
a2920
|
| 2921 |
+
a2921
|
| 2922 |
+
a2922
|
| 2923 |
+
a2923
|
| 2924 |
+
a2924
|
| 2925 |
+
a2925
|
| 2926 |
+
a2926
|
| 2927 |
+
a2927
|
| 2928 |
+
a2928
|
| 2929 |
+
a2929
|
| 2930 |
+
a2930
|
| 2931 |
+
a2931
|
| 2932 |
+
a2932
|
| 2933 |
+
a2933
|
| 2934 |
+
a2934
|
| 2935 |
+
a2935
|
| 2936 |
+
a2936
|
| 2937 |
+
a2937
|
| 2938 |
+
a2938
|
| 2939 |
+
a2939
|
| 2940 |
+
a2940
|
| 2941 |
+
a2941
|
| 2942 |
+
a2942
|
| 2943 |
+
a2943
|
| 2944 |
+
a2944
|
| 2945 |
+
a2945
|
| 2946 |
+
a2946
|
| 2947 |
+
a2947
|
| 2948 |
+
a2948
|
| 2949 |
+
a2949
|
| 2950 |
+
a2950
|
| 2951 |
+
a2951
|
| 2952 |
+
a2952
|
| 2953 |
+
a2953
|
| 2954 |
+
a2954
|
| 2955 |
+
a2955
|
| 2956 |
+
a2956
|
| 2957 |
+
a2957
|
| 2958 |
+
a2958
|
| 2959 |
+
a2959
|
| 2960 |
+
a2960
|
| 2961 |
+
a2961
|
| 2962 |
+
a2962
|
| 2963 |
+
a2963
|
| 2964 |
+
a2964
|
| 2965 |
+
a2965
|
| 2966 |
+
a2966
|
| 2967 |
+
a2967
|
| 2968 |
+
a2968
|
| 2969 |
+
a2969
|
| 2970 |
+
a2970
|
| 2971 |
+
a2971
|
| 2972 |
+
a2972
|
| 2973 |
+
a2973
|
| 2974 |
+
a2974
|
| 2975 |
+
a2975
|
| 2976 |
+
a2976
|
| 2977 |
+
a2977
|
| 2978 |
+
a2978
|
| 2979 |
+
a2979
|
| 2980 |
+
a2980
|
| 2981 |
+
a2981
|
| 2982 |
+
a2982
|
| 2983 |
+
a2983
|
| 2984 |
+
a2984
|
| 2985 |
+
a2985
|
| 2986 |
+
a2986
|
| 2987 |
+
a2987
|
| 2988 |
+
a2988
|
| 2989 |
+
a2989
|
| 2990 |
+
a2990
|
| 2991 |
+
a2991
|
| 2992 |
+
a2992
|
| 2993 |
+
a2993
|
| 2994 |
+
a2994
|
| 2995 |
+
a2995
|
| 2996 |
+
a2996
|
| 2997 |
+
a2997
|
| 2998 |
+
a2998
|
| 2999 |
+
a2999
|
| 3000 |
+
a3000
|
| 3001 |
+
a3001
|
| 3002 |
+
a3002
|
| 3003 |
+
a3003
|
| 3004 |
+
a3004
|
| 3005 |
+
a3005
|
| 3006 |
+
a3006
|
| 3007 |
+
a3007
|
| 3008 |
+
a3008
|
| 3009 |
+
a3009
|
| 3010 |
+
a3010
|
| 3011 |
+
a3011
|
| 3012 |
+
a3012
|
| 3013 |
+
a3013
|
| 3014 |
+
a3014
|
| 3015 |
+
a3015
|
| 3016 |
+
a3016
|
| 3017 |
+
a3017
|
| 3018 |
+
a3018
|
| 3019 |
+
a3019
|
| 3020 |
+
a3020
|
| 3021 |
+
a3021
|
| 3022 |
+
a3022
|
| 3023 |
+
a3023
|
| 3024 |
+
a3024
|
| 3025 |
+
a3025
|
| 3026 |
+
a3026
|
| 3027 |
+
a3027
|
| 3028 |
+
a3028
|
| 3029 |
+
a3029
|
| 3030 |
+
a3030
|
| 3031 |
+
a3031
|
| 3032 |
+
a3032
|
| 3033 |
+
a3033
|
| 3034 |
+
a3034
|
| 3035 |
+
a3035
|
| 3036 |
+
a3036
|
| 3037 |
+
a3037
|
| 3038 |
+
a3038
|
| 3039 |
+
a3039
|
| 3040 |
+
a3040
|
| 3041 |
+
a3041
|
| 3042 |
+
a3042
|
| 3043 |
+
a3043
|
| 3044 |
+
a3044
|
| 3045 |
+
a3045
|
| 3046 |
+
a3046
|
| 3047 |
+
a3047
|
| 3048 |
+
a3048
|
| 3049 |
+
a3049
|
| 3050 |
+
a3050
|
| 3051 |
+
a3051
|
| 3052 |
+
a3052
|
| 3053 |
+
a3053
|
| 3054 |
+
a3054
|
| 3055 |
+
a3055
|
| 3056 |
+
a3056
|
| 3057 |
+
a3057
|
| 3058 |
+
a3058
|
| 3059 |
+
a3059
|
| 3060 |
+
a3060
|
| 3061 |
+
a3061
|
| 3062 |
+
a3062
|
| 3063 |
+
a3063
|
| 3064 |
+
a3064
|
| 3065 |
+
a3065
|
| 3066 |
+
a3066
|
| 3067 |
+
a3067
|
| 3068 |
+
a3068
|
| 3069 |
+
a3069
|
| 3070 |
+
a3070
|
| 3071 |
+
a3071
|
| 3072 |
+
a3072
|
| 3073 |
+
a3073
|
| 3074 |
+
a3074
|
| 3075 |
+
a3075
|
| 3076 |
+
a3076
|
| 3077 |
+
a3077
|
| 3078 |
+
a3078
|
| 3079 |
+
a3079
|
| 3080 |
+
a3080
|
| 3081 |
+
a3081
|
| 3082 |
+
a3082
|
| 3083 |
+
a3083
|
| 3084 |
+
a3084
|
| 3085 |
+
a3085
|
| 3086 |
+
a3086
|
| 3087 |
+
a3087
|
| 3088 |
+
a3088
|
| 3089 |
+
a3089
|
| 3090 |
+
a3090
|
| 3091 |
+
a3091
|
| 3092 |
+
a3092
|
| 3093 |
+
a3093
|
| 3094 |
+
a3094
|
| 3095 |
+
a3095
|
| 3096 |
+
a3096
|
| 3097 |
+
a3097
|
| 3098 |
+
a3098
|
| 3099 |
+
a3099
|
| 3100 |
+
a3100
|
| 3101 |
+
a3101
|
| 3102 |
+
a3102
|
| 3103 |
+
a3103
|
| 3104 |
+
a3104
|
| 3105 |
+
a3105
|
| 3106 |
+
a3106
|
| 3107 |
+
a3107
|
| 3108 |
+
a3108
|
| 3109 |
+
a3109
|
| 3110 |
+
a3110
|
| 3111 |
+
a3111
|
| 3112 |
+
a3112
|
| 3113 |
+
a3113
|
| 3114 |
+
a3114
|
| 3115 |
+
a3115
|
| 3116 |
+
a3116
|
| 3117 |
+
a3117
|
| 3118 |
+
a3118
|
| 3119 |
+
a3119
|
| 3120 |
+
a3120
|
| 3121 |
+
a3121
|
| 3122 |
+
a3122
|
| 3123 |
+
a3123
|
| 3124 |
+
a3124
|
| 3125 |
+
a3125
|
| 3126 |
+
a3126
|
| 3127 |
+
a3127
|
| 3128 |
+
a3128
|
| 3129 |
+
a3129
|
| 3130 |
+
a3130
|
| 3131 |
+
a3131
|
| 3132 |
+
a3132
|
| 3133 |
+
a3133
|
| 3134 |
+
a3134
|
| 3135 |
+
a3135
|
| 3136 |
+
a3136
|
| 3137 |
+
a3137
|
| 3138 |
+
a3138
|
| 3139 |
+
a3139
|
| 3140 |
+
a3140
|
| 3141 |
+
a3141
|
| 3142 |
+
a3142
|
| 3143 |
+
a3143
|
| 3144 |
+
a3144
|
| 3145 |
+
a3145
|
| 3146 |
+
a3146
|
| 3147 |
+
a3147
|
| 3148 |
+
a3148
|
| 3149 |
+
a3149
|
| 3150 |
+
a3150
|
| 3151 |
+
a3151
|
| 3152 |
+
a3152
|
| 3153 |
+
a3153
|
| 3154 |
+
a3154
|
| 3155 |
+
a3155
|
| 3156 |
+
a3156
|
| 3157 |
+
a3157
|
| 3158 |
+
a3158
|
| 3159 |
+
a3159
|
| 3160 |
+
a3160
|
| 3161 |
+
a3161
|
| 3162 |
+
a3162
|
| 3163 |
+
a3163
|
| 3164 |
+
a3164
|
| 3165 |
+
a3165
|
| 3166 |
+
a3166
|
| 3167 |
+
a3167
|
| 3168 |
+
a3168
|
| 3169 |
+
a3169
|
| 3170 |
+
a3170
|
| 3171 |
+
a3171
|
| 3172 |
+
a3172
|
| 3173 |
+
a3173
|
| 3174 |
+
a3174
|
| 3175 |
+
a3175
|
| 3176 |
+
a3176
|
| 3177 |
+
a3177
|
| 3178 |
+
a3178
|
| 3179 |
+
a3179
|
| 3180 |
+
a3180
|
| 3181 |
+
a3181
|
| 3182 |
+
a3182
|
| 3183 |
+
a3183
|
| 3184 |
+
a3184
|
| 3185 |
+
a3185
|
| 3186 |
+
a3186
|
| 3187 |
+
a3187
|
| 3188 |
+
a3188
|
| 3189 |
+
a3189
|
| 3190 |
+
a3190
|
| 3191 |
+
a3191
|
| 3192 |
+
a3192
|
| 3193 |
+
a3193
|
| 3194 |
+
a3194
|
| 3195 |
+
a3195
|
| 3196 |
+
a3196
|
| 3197 |
+
a3197
|
| 3198 |
+
a3198
|
| 3199 |
+
a3199
|
| 3200 |
+
a3200
|
| 3201 |
+
a3201
|
| 3202 |
+
a3202
|
| 3203 |
+
a3203
|
| 3204 |
+
a3204
|
| 3205 |
+
a3205
|
| 3206 |
+
a3206
|
| 3207 |
+
a3207
|
| 3208 |
+
a3208
|
| 3209 |
+
a3209
|
| 3210 |
+
a3210
|
| 3211 |
+
a3211
|
| 3212 |
+
a3212
|
| 3213 |
+
a3213
|
| 3214 |
+
a3214
|
| 3215 |
+
a3215
|
| 3216 |
+
a3216
|
| 3217 |
+
a3217
|
| 3218 |
+
a3218
|
| 3219 |
+
a3219
|
| 3220 |
+
a3220
|
| 3221 |
+
a3221
|
| 3222 |
+
a3222
|
| 3223 |
+
a3223
|
| 3224 |
+
a3224
|
| 3225 |
+
a3225
|
| 3226 |
+
a3226
|
| 3227 |
+
a3227
|
| 3228 |
+
a3228
|
| 3229 |
+
a3229
|
| 3230 |
+
a3230
|
| 3231 |
+
a3231
|
| 3232 |
+
a3232
|
| 3233 |
+
a3233
|
| 3234 |
+
a3234
|
| 3235 |
+
a3235
|
| 3236 |
+
a3236
|
| 3237 |
+
a3237
|
| 3238 |
+
a3238
|
| 3239 |
+
a3239
|
| 3240 |
+
a3240
|
| 3241 |
+
a3241
|
| 3242 |
+
a3242
|
| 3243 |
+
a3243
|
| 3244 |
+
a3244
|
| 3245 |
+
a3245
|
| 3246 |
+
a3246
|
| 3247 |
+
a3247
|
| 3248 |
+
a3248
|
| 3249 |
+
a3249
|
| 3250 |
+
a3250
|
| 3251 |
+
a3251
|
| 3252 |
+
a3252
|
| 3253 |
+
a3253
|
| 3254 |
+
a3254
|
| 3255 |
+
a3255
|
| 3256 |
+
a3256
|
| 3257 |
+
a3257
|
| 3258 |
+
a3258
|
| 3259 |
+
a3259
|
| 3260 |
+
a3260
|
| 3261 |
+
a3261
|
| 3262 |
+
a3262
|
| 3263 |
+
a3263
|
| 3264 |
+
a3264
|
| 3265 |
+
a3265
|
| 3266 |
+
a3266
|
| 3267 |
+
a3267
|
| 3268 |
+
a3268
|
| 3269 |
+
a3269
|
| 3270 |
+
a3270
|
| 3271 |
+
a3271
|
| 3272 |
+
a3272
|
| 3273 |
+
a3273
|
| 3274 |
+
a3274
|
| 3275 |
+
a3275
|
| 3276 |
+
a3276
|
| 3277 |
+
a3277
|
| 3278 |
+
a3278
|
| 3279 |
+
a3279
|
| 3280 |
+
a3280
|
| 3281 |
+
a3281
|
| 3282 |
+
a3282
|
| 3283 |
+
a3283
|
| 3284 |
+
a3284
|
| 3285 |
+
a3285
|
| 3286 |
+
a3286
|
| 3287 |
+
a3287
|
| 3288 |
+
a3288
|
| 3289 |
+
a3289
|
| 3290 |
+
a3290
|
| 3291 |
+
a3291
|
| 3292 |
+
a3292
|
| 3293 |
+
a3293
|
| 3294 |
+
a3294
|
| 3295 |
+
a3295
|
| 3296 |
+
a3296
|
| 3297 |
+
a3297
|
| 3298 |
+
a3298
|
| 3299 |
+
a3299
|
| 3300 |
+
a3300
|
| 3301 |
+
a3301
|
| 3302 |
+
a3302
|
| 3303 |
+
a3303
|
| 3304 |
+
a3304
|
| 3305 |
+
a3305
|
| 3306 |
+
a3306
|
| 3307 |
+
a3307
|
| 3308 |
+
a3308
|
| 3309 |
+
a3309
|
| 3310 |
+
a3310
|
| 3311 |
+
a3311
|
| 3312 |
+
a3312
|
| 3313 |
+
a3313
|
| 3314 |
+
a3314
|
| 3315 |
+
a3315
|
| 3316 |
+
a3316
|
| 3317 |
+
a3317
|
| 3318 |
+
a3318
|
| 3319 |
+
a3319
|
| 3320 |
+
a3320
|
| 3321 |
+
a3321
|
| 3322 |
+
a3322
|
| 3323 |
+
a3323
|
| 3324 |
+
a3324
|
| 3325 |
+
a3325
|
| 3326 |
+
a3326
|
| 3327 |
+
a3327
|
| 3328 |
+
a3328
|
| 3329 |
+
a3329
|
| 3330 |
+
a3330
|
| 3331 |
+
a3331
|
| 3332 |
+
a3332
|
| 3333 |
+
a3333
|
| 3334 |
+
a3334
|
| 3335 |
+
a3335
|
| 3336 |
+
a3336
|
| 3337 |
+
a3337
|
| 3338 |
+
a3338
|
| 3339 |
+
a3339
|
| 3340 |
+
a3340
|
| 3341 |
+
a3341
|
| 3342 |
+
a3342
|
| 3343 |
+
a3343
|
| 3344 |
+
a3344
|
| 3345 |
+
a3345
|
| 3346 |
+
a3346
|
| 3347 |
+
a3347
|
| 3348 |
+
a3348
|
| 3349 |
+
a3349
|
| 3350 |
+
a3350
|
| 3351 |
+
a3351
|
| 3352 |
+
a3352
|
| 3353 |
+
a3353
|
| 3354 |
+
a3354
|
| 3355 |
+
a3355
|
| 3356 |
+
a3356
|
| 3357 |
+
a3357
|
| 3358 |
+
a3358
|
| 3359 |
+
a3359
|
| 3360 |
+
a3360
|
| 3361 |
+
a3361
|
| 3362 |
+
a3362
|
| 3363 |
+
a3363
|
| 3364 |
+
a3364
|
| 3365 |
+
a3365
|
| 3366 |
+
a3366
|
| 3367 |
+
a3367
|
| 3368 |
+
a3368
|
| 3369 |
+
a3369
|
| 3370 |
+
a3370
|
| 3371 |
+
a3371
|
| 3372 |
+
a3372
|
| 3373 |
+
a3373
|
| 3374 |
+
a3374
|
| 3375 |
+
a3375
|
| 3376 |
+
a3376
|
| 3377 |
+
a3377
|
| 3378 |
+
a3378
|
| 3379 |
+
a3379
|
| 3380 |
+
a3380
|
| 3381 |
+
a3381
|
| 3382 |
+
a3382
|
| 3383 |
+
a3383
|
| 3384 |
+
a3384
|
| 3385 |
+
a3385
|
| 3386 |
+
a3386
|
| 3387 |
+
a3387
|
| 3388 |
+
a3388
|
| 3389 |
+
a3389
|
| 3390 |
+
a3390
|
| 3391 |
+
a3391
|
| 3392 |
+
a3392
|
| 3393 |
+
a3393
|
| 3394 |
+
a3394
|
| 3395 |
+
a3395
|
| 3396 |
+
a3396
|
| 3397 |
+
a3397
|
| 3398 |
+
a3398
|
| 3399 |
+
a3399
|
| 3400 |
+
a3400
|
| 3401 |
+
a3401
|
| 3402 |
+
a3402
|
| 3403 |
+
a3403
|
| 3404 |
+
a3404
|
| 3405 |
+
a3405
|
| 3406 |
+
a3406
|
| 3407 |
+
a3407
|
| 3408 |
+
a3408
|
| 3409 |
+
a3409
|
| 3410 |
+
a3410
|
| 3411 |
+
a3411
|
| 3412 |
+
a3412
|
| 3413 |
+
a3413
|
| 3414 |
+
a3414
|
| 3415 |
+
a3415
|
| 3416 |
+
a3416
|
| 3417 |
+
a3417
|
| 3418 |
+
a3418
|
| 3419 |
+
a3419
|
| 3420 |
+
a3420
|
| 3421 |
+
a3421
|
| 3422 |
+
a3422
|
| 3423 |
+
a3423
|
| 3424 |
+
a3424
|
| 3425 |
+
a3425
|
| 3426 |
+
a3426
|
| 3427 |
+
a3427
|
| 3428 |
+
a3428
|
| 3429 |
+
a3429
|
| 3430 |
+
a3430
|
| 3431 |
+
a3431
|
| 3432 |
+
a3432
|
| 3433 |
+
a3433
|
| 3434 |
+
a3434
|
| 3435 |
+
a3435
|
| 3436 |
+
a3436
|
| 3437 |
+
a3437
|
| 3438 |
+
a3438
|
| 3439 |
+
a3439
|
| 3440 |
+
a3440
|
| 3441 |
+
a3441
|
| 3442 |
+
a3442
|
| 3443 |
+
a3443
|
| 3444 |
+
a3444
|
| 3445 |
+
a3445
|
| 3446 |
+
a3446
|
| 3447 |
+
a3447
|
| 3448 |
+
a3448
|
| 3449 |
+
a3449
|
| 3450 |
+
a3450
|
| 3451 |
+
a3451
|
| 3452 |
+
a3452
|
| 3453 |
+
a3453
|
| 3454 |
+
a3454
|
| 3455 |
+
a3455
|
| 3456 |
+
a3456
|
| 3457 |
+
a3457
|
| 3458 |
+
a3458
|
| 3459 |
+
a3459
|
| 3460 |
+
a3460
|
| 3461 |
+
a3461
|
| 3462 |
+
a3462
|
| 3463 |
+
a3463
|
| 3464 |
+
a3464
|
| 3465 |
+
a3465
|
| 3466 |
+
a3466
|
| 3467 |
+
a3467
|
| 3468 |
+
a3468
|
| 3469 |
+
a3469
|
| 3470 |
+
a3470
|
| 3471 |
+
a3471
|
| 3472 |
+
a3472
|
| 3473 |
+
a3473
|
| 3474 |
+
a3474
|
| 3475 |
+
a3475
|
| 3476 |
+
a3476
|
| 3477 |
+
a3477
|
| 3478 |
+
a3478
|
| 3479 |
+
a3479
|
| 3480 |
+
a3480
|
| 3481 |
+
a3481
|
| 3482 |
+
a3482
|
| 3483 |
+
a3483
|
| 3484 |
+
a3484
|
| 3485 |
+
a3485
|
| 3486 |
+
a3486
|
| 3487 |
+
a3487
|
| 3488 |
+
a3488
|
| 3489 |
+
a3489
|
| 3490 |
+
a3490
|
| 3491 |
+
a3491
|
| 3492 |
+
a3492
|
| 3493 |
+
a3493
|
| 3494 |
+
a3494
|
| 3495 |
+
a3495
|
| 3496 |
+
a3496
|
| 3497 |
+
a3497
|
| 3498 |
+
a3498
|
| 3499 |
+
a3499
|
| 3500 |
+
a3500
|
| 3501 |
+
a3501
|
| 3502 |
+
a3502
|
| 3503 |
+
a3503
|
| 3504 |
+
a3504
|
| 3505 |
+
a3505
|
| 3506 |
+
a3506
|
| 3507 |
+
a3507
|
| 3508 |
+
a3508
|
| 3509 |
+
a3509
|
| 3510 |
+
a3510
|
| 3511 |
+
a3511
|
| 3512 |
+
a3512
|
| 3513 |
+
a3513
|
| 3514 |
+
a3514
|
| 3515 |
+
a3515
|
| 3516 |
+
a3516
|
| 3517 |
+
a3517
|
| 3518 |
+
a3518
|
| 3519 |
+
a3519
|
| 3520 |
+
a3520
|
| 3521 |
+
a3521
|
| 3522 |
+
a3522
|
| 3523 |
+
a3523
|
| 3524 |
+
a3524
|
| 3525 |
+
a3525
|
| 3526 |
+
a3526
|
| 3527 |
+
a3527
|
| 3528 |
+
a3528
|
| 3529 |
+
a3529
|
| 3530 |
+
a3530
|
| 3531 |
+
a3531
|
| 3532 |
+
a3532
|
| 3533 |
+
a3533
|
| 3534 |
+
a3534
|
| 3535 |
+
a3535
|
| 3536 |
+
a3536
|
| 3537 |
+
a3537
|
| 3538 |
+
a3538
|
| 3539 |
+
a3539
|
| 3540 |
+
a3540
|
| 3541 |
+
a3541
|
| 3542 |
+
a3542
|
| 3543 |
+
a3543
|
| 3544 |
+
a3544
|
| 3545 |
+
a3545
|
| 3546 |
+
a3546
|
| 3547 |
+
a3547
|
| 3548 |
+
a3548
|
| 3549 |
+
a3549
|
| 3550 |
+
a3550
|
| 3551 |
+
a3551
|
| 3552 |
+
a3552
|
| 3553 |
+
a3553
|
| 3554 |
+
a3554
|
| 3555 |
+
a3555
|
| 3556 |
+
a3556
|
| 3557 |
+
a3557
|
| 3558 |
+
a3558
|
| 3559 |
+
a3559
|
| 3560 |
+
a3560
|
| 3561 |
+
a3561
|
| 3562 |
+
a3562
|
| 3563 |
+
a3563
|
| 3564 |
+
a3564
|
| 3565 |
+
a3565
|
| 3566 |
+
a3566
|
| 3567 |
+
a3567
|
| 3568 |
+
a3568
|
| 3569 |
+
a3569
|
| 3570 |
+
a3570
|
| 3571 |
+
a3571
|
| 3572 |
+
a3572
|
| 3573 |
+
a3573
|
| 3574 |
+
a3574
|
| 3575 |
+
a3575
|
| 3576 |
+
a3576
|
| 3577 |
+
a3577
|
| 3578 |
+
a3578
|
| 3579 |
+
a3579
|
| 3580 |
+
a3580
|
| 3581 |
+
a3581
|
| 3582 |
+
a3582
|
| 3583 |
+
a3583
|
| 3584 |
+
a3584
|
| 3585 |
+
a3585
|
| 3586 |
+
a3586
|
| 3587 |
+
a3587
|
| 3588 |
+
a3588
|
| 3589 |
+
a3589
|
| 3590 |
+
a3590
|
| 3591 |
+
a3591
|
| 3592 |
+
a3592
|
| 3593 |
+
a3593
|
| 3594 |
+
a3594
|
| 3595 |
+
a3595
|
| 3596 |
+
a3596
|
| 3597 |
+
a3597
|
| 3598 |
+
a3598
|
| 3599 |
+
a3599
|
| 3600 |
+
a3600
|
| 3601 |
+
a3601
|
| 3602 |
+
a3602
|
| 3603 |
+
a3603
|
| 3604 |
+
a3604
|
| 3605 |
+
a3605
|
| 3606 |
+
a3606
|
| 3607 |
+
a3607
|
| 3608 |
+
a3608
|
| 3609 |
+
a3609
|
| 3610 |
+
a3610
|
| 3611 |
+
a3611
|
| 3612 |
+
a3612
|
| 3613 |
+
a3613
|
| 3614 |
+
a3614
|
| 3615 |
+
a3615
|
| 3616 |
+
a3616
|
| 3617 |
+
a3617
|
| 3618 |
+
a3618
|
| 3619 |
+
a3619
|
| 3620 |
+
a3620
|
| 3621 |
+
a3621
|
| 3622 |
+
a3622
|
| 3623 |
+
a3623
|
| 3624 |
+
a3624
|
| 3625 |
+
a3625
|
| 3626 |
+
a3626
|
| 3627 |
+
a3627
|
| 3628 |
+
a3628
|
| 3629 |
+
a3629
|
| 3630 |
+
a3630
|
| 3631 |
+
a3631
|
| 3632 |
+
a3632
|
| 3633 |
+
a3633
|
| 3634 |
+
a3634
|
| 3635 |
+
a3635
|
| 3636 |
+
a3636
|
| 3637 |
+
a3637
|
| 3638 |
+
a3638
|
| 3639 |
+
a3639
|
| 3640 |
+
a3640
|
| 3641 |
+
a3641
|
| 3642 |
+
a3642
|
| 3643 |
+
a3643
|
| 3644 |
+
a3644
|
| 3645 |
+
a3645
|
| 3646 |
+
a3646
|
| 3647 |
+
a3647
|
| 3648 |
+
a3648
|
| 3649 |
+
a3649
|
| 3650 |
+
a3650
|
| 3651 |
+
a3651
|
| 3652 |
+
a3652
|
| 3653 |
+
a3653
|
| 3654 |
+
a3654
|
| 3655 |
+
a3655
|
| 3656 |
+
a3656
|
| 3657 |
+
a3657
|
| 3658 |
+
a3658
|
| 3659 |
+
a3659
|
| 3660 |
+
a3660
|
| 3661 |
+
a3661
|
| 3662 |
+
a3662
|
| 3663 |
+
a3663
|
| 3664 |
+
a3664
|
| 3665 |
+
a3665
|
| 3666 |
+
a3666
|
| 3667 |
+
a3667
|
| 3668 |
+
a3668
|
| 3669 |
+
a3669
|
| 3670 |
+
a3670
|
| 3671 |
+
a3671
|
| 3672 |
+
a3672
|
| 3673 |
+
a3673
|
| 3674 |
+
a3674
|
| 3675 |
+
a3675
|
| 3676 |
+
a3676
|
| 3677 |
+
a3677
|
| 3678 |
+
a3678
|
| 3679 |
+
a3679
|
| 3680 |
+
a3680
|
| 3681 |
+
a3681
|
| 3682 |
+
a3682
|
| 3683 |
+
a3683
|
| 3684 |
+
a3684
|
| 3685 |
+
a3685
|
| 3686 |
+
a3686
|
| 3687 |
+
a3687
|
| 3688 |
+
a3688
|
| 3689 |
+
a3689
|
| 3690 |
+
a3690
|
| 3691 |
+
a3691
|
| 3692 |
+
a3692
|
| 3693 |
+
a3693
|
| 3694 |
+
a3694
|
| 3695 |
+
a3695
|
| 3696 |
+
a3696
|
| 3697 |
+
a3697
|
| 3698 |
+
a3698
|
| 3699 |
+
a3699
|
| 3700 |
+
a3700
|
| 3701 |
+
a3701
|
| 3702 |
+
a3702
|
| 3703 |
+
a3703
|
| 3704 |
+
a3704
|
| 3705 |
+
a3705
|
| 3706 |
+
a3706
|
| 3707 |
+
a3707
|
| 3708 |
+
a3708
|
| 3709 |
+
a3709
|
| 3710 |
+
a3710
|
| 3711 |
+
a3711
|
| 3712 |
+
a3712
|
| 3713 |
+
a3713
|
| 3714 |
+
a3714
|
| 3715 |
+
a3715
|
| 3716 |
+
a3716
|
| 3717 |
+
a3717
|
| 3718 |
+
a3718
|
| 3719 |
+
a3719
|
| 3720 |
+
a3720
|
| 3721 |
+
a3721
|
| 3722 |
+
a3722
|
| 3723 |
+
a3723
|
| 3724 |
+
a3724
|
| 3725 |
+
a3725
|
| 3726 |
+
a3726
|
| 3727 |
+
a3727
|
| 3728 |
+
a3728
|
| 3729 |
+
a3729
|
| 3730 |
+
a3730
|
| 3731 |
+
a3731
|
| 3732 |
+
a3732
|
| 3733 |
+
a3733
|
| 3734 |
+
a3734
|
| 3735 |
+
a3735
|
| 3736 |
+
a3736
|
| 3737 |
+
a3737
|
| 3738 |
+
a3738
|
| 3739 |
+
a3739
|
| 3740 |
+
a3740
|
| 3741 |
+
a3741
|
| 3742 |
+
a3742
|
| 3743 |
+
a3743
|
| 3744 |
+
a3744
|
| 3745 |
+
a3745
|
| 3746 |
+
a3746
|
| 3747 |
+
a3747
|
| 3748 |
+
a3748
|
| 3749 |
+
a3749
|
| 3750 |
+
a3750
|
| 3751 |
+
a3751
|
| 3752 |
+
a3752
|
| 3753 |
+
a3753
|
| 3754 |
+
a3754
|
| 3755 |
+
a3755
|
| 3756 |
+
a3756
|
| 3757 |
+
a3757
|
| 3758 |
+
a3758
|
| 3759 |
+
a3759
|
| 3760 |
+
a3760
|
| 3761 |
+
a3761
|
| 3762 |
+
a3762
|
| 3763 |
+
a3763
|
| 3764 |
+
a3764
|
| 3765 |
+
a3765
|
| 3766 |
+
a3766
|
| 3767 |
+
a3767
|
| 3768 |
+
a3768
|
| 3769 |
+
a3769
|
| 3770 |
+
a3770
|
| 3771 |
+
a3771
|
| 3772 |
+
a3772
|
| 3773 |
+
a3773
|
| 3774 |
+
a3774
|
| 3775 |
+
a3775
|
| 3776 |
+
a3776
|
| 3777 |
+
a3777
|
| 3778 |
+
a3778
|
| 3779 |
+
a3779
|
| 3780 |
+
a3780
|
| 3781 |
+
a3781
|
| 3782 |
+
a3782
|
| 3783 |
+
a3783
|
| 3784 |
+
a3784
|
| 3785 |
+
a3785
|
| 3786 |
+
a3786
|
| 3787 |
+
a3787
|
| 3788 |
+
a3788
|
| 3789 |
+
a3789
|
| 3790 |
+
a3790
|
| 3791 |
+
a3791
|
| 3792 |
+
a3792
|
| 3793 |
+
a3793
|
| 3794 |
+
a3794
|
| 3795 |
+
a3795
|
| 3796 |
+
a3796
|
| 3797 |
+
a3797
|
| 3798 |
+
a3798
|
| 3799 |
+
a3799
|
| 3800 |
+
a3800
|
| 3801 |
+
a3801
|
| 3802 |
+
a3802
|
| 3803 |
+
a3803
|
| 3804 |
+
a3804
|
| 3805 |
+
a3805
|
| 3806 |
+
a3806
|
| 3807 |
+
a3807
|
| 3808 |
+
a3808
|
| 3809 |
+
a3809
|
| 3810 |
+
a3810
|
| 3811 |
+
a3811
|
| 3812 |
+
a3812
|
| 3813 |
+
a3813
|
| 3814 |
+
a3814
|
| 3815 |
+
a3815
|
| 3816 |
+
a3816
|
| 3817 |
+
a3817
|
| 3818 |
+
a3818
|
| 3819 |
+
a3819
|
| 3820 |
+
a3820
|
| 3821 |
+
a3821
|
| 3822 |
+
a3822
|
| 3823 |
+
a3823
|
| 3824 |
+
a3824
|
| 3825 |
+
a3825
|
| 3826 |
+
a3826
|
| 3827 |
+
a3827
|
| 3828 |
+
a3828
|
| 3829 |
+
a3829
|
| 3830 |
+
a3830
|
| 3831 |
+
a3831
|
| 3832 |
+
a3832
|
| 3833 |
+
a3833
|
| 3834 |
+
a3834
|
| 3835 |
+
a3835
|
| 3836 |
+
a3836
|
| 3837 |
+
a3837
|
| 3838 |
+
a3838
|
| 3839 |
+
a3839
|
| 3840 |
+
a3840
|
| 3841 |
+
a3841
|
| 3842 |
+
a3842
|
| 3843 |
+
a3843
|
| 3844 |
+
a3844
|
| 3845 |
+
a3845
|
| 3846 |
+
a3846
|
| 3847 |
+
a3847
|
| 3848 |
+
a3848
|
| 3849 |
+
a3849
|
| 3850 |
+
a3850
|
| 3851 |
+
a3851
|
| 3852 |
+
a3852
|
| 3853 |
+
a3853
|
| 3854 |
+
a3854
|
| 3855 |
+
a3855
|
| 3856 |
+
a3856
|
| 3857 |
+
a3857
|
| 3858 |
+
a3858
|
| 3859 |
+
a3859
|
| 3860 |
+
a3860
|
| 3861 |
+
a3861
|
| 3862 |
+
a3862
|
| 3863 |
+
a3863
|
| 3864 |
+
a3864
|
| 3865 |
+
a3865
|
| 3866 |
+
a3866
|
| 3867 |
+
a3867
|
| 3868 |
+
a3868
|
| 3869 |
+
a3869
|
| 3870 |
+
a3870
|
| 3871 |
+
a3871
|
| 3872 |
+
a3872
|
| 3873 |
+
a3873
|
| 3874 |
+
a3874
|
| 3875 |
+
a3875
|
| 3876 |
+
a3876
|
| 3877 |
+
a3877
|
| 3878 |
+
a3878
|
| 3879 |
+
a3879
|
| 3880 |
+
a3880
|
| 3881 |
+
a3881
|
| 3882 |
+
a3882
|
| 3883 |
+
a3883
|
| 3884 |
+
a3884
|
| 3885 |
+
a3885
|
| 3886 |
+
a3886
|
| 3887 |
+
a3887
|
| 3888 |
+
a3888
|
| 3889 |
+
a3889
|
| 3890 |
+
a3890
|
| 3891 |
+
a3891
|
| 3892 |
+
a3892
|
| 3893 |
+
a3893
|
| 3894 |
+
a3894
|
| 3895 |
+
a3895
|
| 3896 |
+
a3896
|
| 3897 |
+
a3897
|
| 3898 |
+
a3898
|
| 3899 |
+
a3899
|
| 3900 |
+
a3900
|
| 3901 |
+
a3901
|
| 3902 |
+
a3902
|
| 3903 |
+
a3903
|
| 3904 |
+
a3904
|
| 3905 |
+
a3905
|
| 3906 |
+
a3906
|
| 3907 |
+
a3907
|
| 3908 |
+
a3908
|
| 3909 |
+
a3909
|
| 3910 |
+
a3910
|
| 3911 |
+
a3911
|
| 3912 |
+
a3912
|
| 3913 |
+
a3913
|
| 3914 |
+
a3914
|
| 3915 |
+
a3915
|
| 3916 |
+
a3916
|
| 3917 |
+
a3917
|
| 3918 |
+
a3918
|
| 3919 |
+
a3919
|
| 3920 |
+
a3920
|
| 3921 |
+
a3921
|
| 3922 |
+
a3922
|
| 3923 |
+
a3923
|
| 3924 |
+
a3924
|
| 3925 |
+
a3925
|
| 3926 |
+
a3926
|
| 3927 |
+
a3927
|
| 3928 |
+
a3928
|
| 3929 |
+
a3929
|
| 3930 |
+
a3930
|
| 3931 |
+
a3931
|
| 3932 |
+
a3932
|
| 3933 |
+
a3933
|
| 3934 |
+
a3934
|
| 3935 |
+
a3935
|
| 3936 |
+
a3936
|
| 3937 |
+
a3937
|
| 3938 |
+
a3938
|
| 3939 |
+
a3939
|
| 3940 |
+
a3940
|
| 3941 |
+
a3941
|
| 3942 |
+
a3942
|
| 3943 |
+
a3943
|
| 3944 |
+
a3944
|
| 3945 |
+
a3945
|
| 3946 |
+
a3946
|
| 3947 |
+
a3947
|
| 3948 |
+
a3948
|
| 3949 |
+
a3949
|
| 3950 |
+
a3950
|
| 3951 |
+
a3951
|
| 3952 |
+
a3952
|
| 3953 |
+
a3953
|
| 3954 |
+
a3954
|
| 3955 |
+
a3955
|
| 3956 |
+
a3956
|
| 3957 |
+
a3957
|
| 3958 |
+
a3958
|
| 3959 |
+
a3959
|
| 3960 |
+
a3960
|
| 3961 |
+
a3961
|
| 3962 |
+
a3962
|
| 3963 |
+
a3963
|
| 3964 |
+
a3964
|
| 3965 |
+
a3965
|
| 3966 |
+
a3966
|
| 3967 |
+
a3967
|
| 3968 |
+
a3968
|
| 3969 |
+
a3969
|
| 3970 |
+
a3970
|
| 3971 |
+
a3971
|
| 3972 |
+
a3972
|
| 3973 |
+
a3973
|
| 3974 |
+
a3974
|
| 3975 |
+
a3975
|
| 3976 |
+
a3976
|
| 3977 |
+
a3977
|
| 3978 |
+
a3978
|
| 3979 |
+
a3979
|
| 3980 |
+
a3980
|
| 3981 |
+
a3981
|
| 3982 |
+
a3982
|
| 3983 |
+
a3983
|
| 3984 |
+
a3984
|
| 3985 |
+
a3985
|
| 3986 |
+
a3986
|
| 3987 |
+
a3987
|
| 3988 |
+
a3988
|
| 3989 |
+
a3989
|
| 3990 |
+
a3990
|
| 3991 |
+
a3991
|
| 3992 |
+
a3992
|
| 3993 |
+
a3993
|
| 3994 |
+
a3994
|
| 3995 |
+
a3995
|
| 3996 |
+
a3996
|
| 3997 |
+
a3997
|
| 3998 |
+
a3998
|
| 3999 |
+
a3999
|
| 4000 |
+
a4000
|
| 4001 |
+
a4001
|
| 4002 |
+
a4002
|
| 4003 |
+
a4003
|
| 4004 |
+
a4004
|
| 4005 |
+
a4005
|
| 4006 |
+
a4006
|
| 4007 |
+
a4007
|
| 4008 |
+
a4008
|
| 4009 |
+
a4009
|
| 4010 |
+
a4010
|
| 4011 |
+
a4011
|
| 4012 |
+
a4012
|
| 4013 |
+
a4013
|
| 4014 |
+
a4014
|
| 4015 |
+
a4015
|
| 4016 |
+
a4016
|
| 4017 |
+
a4017
|
| 4018 |
+
a4018
|
| 4019 |
+
a4019
|
| 4020 |
+
a4020
|
| 4021 |
+
a4021
|
| 4022 |
+
a4022
|
| 4023 |
+
a4023
|
| 4024 |
+
a4024
|
| 4025 |
+
a4025
|
| 4026 |
+
a4026
|
| 4027 |
+
a4027
|
| 4028 |
+
a4028
|
| 4029 |
+
a4029
|
| 4030 |
+
a4030
|
| 4031 |
+
a4031
|
| 4032 |
+
a4032
|
| 4033 |
+
a4033
|
| 4034 |
+
a4034
|
| 4035 |
+
a4035
|
| 4036 |
+
a4036
|
| 4037 |
+
a4037
|
| 4038 |
+
a4038
|
| 4039 |
+
a4039
|
| 4040 |
+
a4040
|
| 4041 |
+
a4041
|
| 4042 |
+
a4042
|
| 4043 |
+
a4043
|
| 4044 |
+
a4044
|
| 4045 |
+
a4045
|
| 4046 |
+
a4046
|
| 4047 |
+
a4047
|
| 4048 |
+
a4048
|
| 4049 |
+
a4049
|
| 4050 |
+
a4050
|
| 4051 |
+
a4051
|
| 4052 |
+
a4052
|
| 4053 |
+
a4053
|
| 4054 |
+
a4054
|
| 4055 |
+
a4055
|
| 4056 |
+
a4056
|
| 4057 |
+
a4057
|
| 4058 |
+
a4058
|
| 4059 |
+
a4059
|
| 4060 |
+
a4060
|
| 4061 |
+
a4061
|
| 4062 |
+
a4062
|
| 4063 |
+
a4063
|
| 4064 |
+
a4064
|
| 4065 |
+
a4065
|
| 4066 |
+
a4066
|
| 4067 |
+
a4067
|
| 4068 |
+
a4068
|
| 4069 |
+
a4069
|
| 4070 |
+
a4070
|
| 4071 |
+
a4071
|
| 4072 |
+
a4072
|
| 4073 |
+
a4073
|
| 4074 |
+
a4074
|
| 4075 |
+
a4075
|
| 4076 |
+
a4076
|
| 4077 |
+
a4077
|
| 4078 |
+
a4078
|
| 4079 |
+
a4079
|
| 4080 |
+
a4080
|
| 4081 |
+
a4081
|
| 4082 |
+
a4082
|
| 4083 |
+
a4083
|
| 4084 |
+
a4084
|
| 4085 |
+
a4085
|
| 4086 |
+
a4086
|
| 4087 |
+
a4087
|
| 4088 |
+
a4088
|
| 4089 |
+
a4089
|
| 4090 |
+
a4090
|
| 4091 |
+
a4091
|
| 4092 |
+
a4092
|
| 4093 |
+
a4093
|
| 4094 |
+
a4094
|
| 4095 |
+
a4095
|
| 4096 |
+
a4096
|
| 4097 |
+
a4097
|
| 4098 |
+
a4098
|
| 4099 |
+
a4099
|
| 4100 |
+
a4100
|
| 4101 |
+
a4101
|
| 4102 |
+
a4102
|
| 4103 |
+
a4103
|
| 4104 |
+
a4104
|
| 4105 |
+
a4105
|
| 4106 |
+
a4106
|
| 4107 |
+
a4107
|
| 4108 |
+
a4108
|
| 4109 |
+
a4109
|
| 4110 |
+
a4110
|
| 4111 |
+
a4111
|
| 4112 |
+
a4112
|
| 4113 |
+
a4113
|
| 4114 |
+
a4114
|
| 4115 |
+
a4115
|
| 4116 |
+
a4116
|
| 4117 |
+
a4117
|
| 4118 |
+
a4118
|
| 4119 |
+
a4119
|
| 4120 |
+
a4120
|
| 4121 |
+
a4121
|
| 4122 |
+
a4122
|
| 4123 |
+
a4123
|
| 4124 |
+
a4124
|
| 4125 |
+
a4125
|
| 4126 |
+
a4126
|
| 4127 |
+
a4127
|
| 4128 |
+
a4128
|
| 4129 |
+
a4129
|
| 4130 |
+
a4130
|
| 4131 |
+
a4131
|
| 4132 |
+
a4132
|
| 4133 |
+
a4133
|
| 4134 |
+
a4134
|
| 4135 |
+
a4135
|
| 4136 |
+
a4136
|
| 4137 |
+
a4137
|
| 4138 |
+
a4138
|
| 4139 |
+
a4139
|
| 4140 |
+
a4140
|
| 4141 |
+
a4141
|
| 4142 |
+
a4142
|
| 4143 |
+
a4143
|
| 4144 |
+
a4144
|
| 4145 |
+
a4145
|
| 4146 |
+
a4146
|
| 4147 |
+
a4147
|
| 4148 |
+
a4148
|
| 4149 |
+
a4149
|
| 4150 |
+
a4150
|
| 4151 |
+
a4151
|
| 4152 |
+
a4152
|
| 4153 |
+
a4153
|
| 4154 |
+
a4154
|
| 4155 |
+
a4155
|
| 4156 |
+
a4156
|
| 4157 |
+
a4157
|
| 4158 |
+
a4158
|
| 4159 |
+
a4159
|
| 4160 |
+
a4160
|
| 4161 |
+
a4161
|
| 4162 |
+
a4162
|
| 4163 |
+
a4163
|
| 4164 |
+
a4164
|
| 4165 |
+
a4165
|
| 4166 |
+
a4166
|
| 4167 |
+
a4167
|
| 4168 |
+
a4168
|
| 4169 |
+
a4169
|
| 4170 |
+
a4170
|
| 4171 |
+
a4171
|
| 4172 |
+
a4172
|
| 4173 |
+
a4173
|
| 4174 |
+
a4174
|
| 4175 |
+
a4175
|
| 4176 |
+
a4176
|
| 4177 |
+
a4177
|
| 4178 |
+
a4178
|
| 4179 |
+
a4179
|
| 4180 |
+
a4180
|
| 4181 |
+
a4181
|
| 4182 |
+
a4182
|
| 4183 |
+
a4183
|
| 4184 |
+
a4184
|
| 4185 |
+
a4185
|
| 4186 |
+
a4186
|
| 4187 |
+
a4187
|
| 4188 |
+
a4188
|
| 4189 |
+
a4189
|
| 4190 |
+
a4190
|
| 4191 |
+
a4191
|
| 4192 |
+
a4192
|
| 4193 |
+
a4193
|
| 4194 |
+
a4194
|
| 4195 |
+
a4195
|
| 4196 |
+
a4196
|
| 4197 |
+
a4197
|
| 4198 |
+
a4198
|
| 4199 |
+
a4199
|
| 4200 |
+
a4200
|
| 4201 |
+
a4201
|
| 4202 |
+
a4202
|
| 4203 |
+
a4203
|
| 4204 |
+
a4204
|
| 4205 |
+
a4205
|
| 4206 |
+
a4206
|
| 4207 |
+
a4207
|
| 4208 |
+
a4208
|
| 4209 |
+
a4209
|
| 4210 |
+
a4210
|
| 4211 |
+
a4211
|
| 4212 |
+
a4212
|
| 4213 |
+
a4213
|
| 4214 |
+
a4214
|
| 4215 |
+
a4215
|
| 4216 |
+
a4216
|
| 4217 |
+
a4217
|
| 4218 |
+
a4218
|
| 4219 |
+
a4219
|
| 4220 |
+
a4220
|
| 4221 |
+
a4221
|
| 4222 |
+
a4222
|
| 4223 |
+
a4223
|
| 4224 |
+
a4224
|
| 4225 |
+
a4225
|
| 4226 |
+
a4226
|
| 4227 |
+
a4227
|
| 4228 |
+
a4228
|
| 4229 |
+
a4229
|
| 4230 |
+
a4230
|
| 4231 |
+
a4231
|
| 4232 |
+
a4232
|
| 4233 |
+
a4233
|
| 4234 |
+
a4234
|
| 4235 |
+
a4235
|
| 4236 |
+
a4236
|
| 4237 |
+
a4237
|
| 4238 |
+
a4238
|
| 4239 |
+
a4239
|
| 4240 |
+
a4240
|
| 4241 |
+
a4241
|
| 4242 |
+
a4242
|
| 4243 |
+
a4243
|
| 4244 |
+
a4244
|
| 4245 |
+
a4245
|
| 4246 |
+
a4246
|
| 4247 |
+
a4247
|
| 4248 |
+
a4248
|
| 4249 |
+
a4249
|
| 4250 |
+
a4250
|
| 4251 |
+
a4251
|
| 4252 |
+
a4252
|
| 4253 |
+
a4253
|
| 4254 |
+
a4254
|
| 4255 |
+
a4255
|
| 4256 |
+
a4256
|
| 4257 |
+
a4257
|
| 4258 |
+
a4258
|
| 4259 |
+
a4259
|
| 4260 |
+
a4260
|
| 4261 |
+
a4261
|
| 4262 |
+
a4262
|
| 4263 |
+
a4263
|
| 4264 |
+
a4264
|
| 4265 |
+
a4265
|
| 4266 |
+
a4266
|
| 4267 |
+
a4267
|
| 4268 |
+
a4268
|
| 4269 |
+
a4269
|
| 4270 |
+
a4270
|
| 4271 |
+
a4271
|
| 4272 |
+
a4272
|
| 4273 |
+
a4273
|
| 4274 |
+
a4274
|
| 4275 |
+
a4275
|
| 4276 |
+
a4276
|
| 4277 |
+
a4277
|
| 4278 |
+
a4278
|
| 4279 |
+
a4279
|
| 4280 |
+
a4280
|
| 4281 |
+
a4281
|
| 4282 |
+
a4282
|
| 4283 |
+
a4283
|
| 4284 |
+
a4284
|
| 4285 |
+
a4285
|
| 4286 |
+
a4286
|
| 4287 |
+
a4287
|
| 4288 |
+
a4288
|
| 4289 |
+
a4289
|
| 4290 |
+
a4290
|
| 4291 |
+
a4291
|
| 4292 |
+
a4292
|
| 4293 |
+
a4293
|
| 4294 |
+
a4294
|
| 4295 |
+
a4295
|
| 4296 |
+
a4296
|
| 4297 |
+
a4297
|
| 4298 |
+
a4298
|
| 4299 |
+
a4299
|
| 4300 |
+
a4300
|
| 4301 |
+
a4301
|
| 4302 |
+
a4302
|
| 4303 |
+
a4303
|
| 4304 |
+
a4304
|
| 4305 |
+
a4305
|
| 4306 |
+
a4306
|
| 4307 |
+
a4307
|
| 4308 |
+
a4308
|
| 4309 |
+
a4309
|
| 4310 |
+
a4310
|
| 4311 |
+
a4311
|
| 4312 |
+
a4312
|
| 4313 |
+
a4313
|
| 4314 |
+
a4314
|
| 4315 |
+
a4315
|
| 4316 |
+
a4316
|
| 4317 |
+
a4317
|
| 4318 |
+
a4318
|
| 4319 |
+
a4319
|
| 4320 |
+
a4320
|
| 4321 |
+
a4321
|
| 4322 |
+
a4322
|
| 4323 |
+
a4323
|
| 4324 |
+
a4324
|
| 4325 |
+
a4325
|
| 4326 |
+
a4326
|
| 4327 |
+
a4327
|
| 4328 |
+
a4328
|
| 4329 |
+
a4329
|
| 4330 |
+
a4330
|
| 4331 |
+
a4331
|
| 4332 |
+
a4332
|
| 4333 |
+
a4333
|
| 4334 |
+
a4334
|
| 4335 |
+
a4335
|
| 4336 |
+
a4336
|
| 4337 |
+
a4337
|
| 4338 |
+
a4338
|
| 4339 |
+
a4339
|
| 4340 |
+
a4340
|
| 4341 |
+
a4341
|
| 4342 |
+
a4342
|
| 4343 |
+
a4343
|
| 4344 |
+
a4344
|
| 4345 |
+
a4345
|
| 4346 |
+
a4346
|
| 4347 |
+
a4347
|
| 4348 |
+
a4348
|
| 4349 |
+
a4349
|
| 4350 |
+
a4350
|
| 4351 |
+
a4351
|
| 4352 |
+
a4352
|
| 4353 |
+
a4353
|
| 4354 |
+
a4354
|
| 4355 |
+
a4355
|
| 4356 |
+
a4356
|
| 4357 |
+
a4357
|
| 4358 |
+
a4358
|
| 4359 |
+
a4359
|
| 4360 |
+
a4360
|
| 4361 |
+
a4361
|
| 4362 |
+
a4362
|
| 4363 |
+
a4363
|
| 4364 |
+
a4364
|
| 4365 |
+
a4365
|
| 4366 |
+
a4366
|
| 4367 |
+
a4367
|
| 4368 |
+
a4368
|
| 4369 |
+
a4369
|
| 4370 |
+
a4370
|
| 4371 |
+
a4371
|
| 4372 |
+
a4372
|
| 4373 |
+
a4373
|
| 4374 |
+
a4374
|
| 4375 |
+
a4375
|
| 4376 |
+
a4376
|
| 4377 |
+
a4377
|
| 4378 |
+
a4378
|
| 4379 |
+
a4379
|
| 4380 |
+
a4380
|
| 4381 |
+
a4381
|
| 4382 |
+
a4382
|
| 4383 |
+
a4383
|
| 4384 |
+
a4384
|
| 4385 |
+
a4385
|
| 4386 |
+
a4386
|
| 4387 |
+
a4387
|
| 4388 |
+
a4388
|
| 4389 |
+
a4389
|
| 4390 |
+
a4390
|
| 4391 |
+
a4391
|
| 4392 |
+
a4392
|
| 4393 |
+
a4393
|
| 4394 |
+
a4394
|
| 4395 |
+
a4395
|
| 4396 |
+
a4396
|
| 4397 |
+
a4397
|
| 4398 |
+
a4398
|
| 4399 |
+
a4399
|
| 4400 |
+
a4400
|
| 4401 |
+
a4401
|
| 4402 |
+
a4402
|
| 4403 |
+
a4403
|
| 4404 |
+
a4404
|
| 4405 |
+
a4405
|
| 4406 |
+
a4406
|
| 4407 |
+
a4407
|
| 4408 |
+
a4408
|
| 4409 |
+
a4409
|
| 4410 |
+
a4410
|
| 4411 |
+
a4411
|
| 4412 |
+
a4412
|
| 4413 |
+
a4413
|
| 4414 |
+
a4414
|
| 4415 |
+
a4415
|
| 4416 |
+
a4416
|
| 4417 |
+
a4417
|
| 4418 |
+
a4418
|
| 4419 |
+
a4419
|
| 4420 |
+
a4420
|
| 4421 |
+
a4421
|
| 4422 |
+
a4422
|
| 4423 |
+
a4423
|
| 4424 |
+
a4424
|
| 4425 |
+
a4425
|
| 4426 |
+
a4426
|
| 4427 |
+
a4427
|
| 4428 |
+
a4428
|
| 4429 |
+
a4429
|
| 4430 |
+
a4430
|
| 4431 |
+
a4431
|
| 4432 |
+
a4432
|
| 4433 |
+
a4433
|
| 4434 |
+
a4434
|
| 4435 |
+
a4435
|
| 4436 |
+
a4436
|
| 4437 |
+
a4437
|
| 4438 |
+
a4438
|
| 4439 |
+
a4439
|
| 4440 |
+
a4440
|
| 4441 |
+
a4441
|
| 4442 |
+
a4442
|
| 4443 |
+
a4443
|
| 4444 |
+
a4444
|
| 4445 |
+
a4445
|
| 4446 |
+
a4446
|
| 4447 |
+
a4447
|
| 4448 |
+
a4448
|
| 4449 |
+
a4449
|
| 4450 |
+
a4450
|
| 4451 |
+
a4451
|
| 4452 |
+
a4452
|
| 4453 |
+
a4453
|
| 4454 |
+
a4454
|
| 4455 |
+
a4455
|
| 4456 |
+
a4456
|
| 4457 |
+
a4457
|
| 4458 |
+
a4458
|
| 4459 |
+
a4459
|
| 4460 |
+
a4460
|
| 4461 |
+
a4461
|
| 4462 |
+
a4462
|
| 4463 |
+
a4463
|
| 4464 |
+
a4464
|
| 4465 |
+
a4465
|
| 4466 |
+
a4466
|
| 4467 |
+
a4467
|
| 4468 |
+
a4468
|
| 4469 |
+
a4469
|
| 4470 |
+
a4470
|
| 4471 |
+
a4471
|
| 4472 |
+
a4472
|
| 4473 |
+
a4473
|
| 4474 |
+
a4474
|
| 4475 |
+
a4475
|
| 4476 |
+
a4476
|
| 4477 |
+
a4477
|
| 4478 |
+
a4478
|
| 4479 |
+
a4479
|
| 4480 |
+
a4480
|
| 4481 |
+
a4481
|
| 4482 |
+
a4482
|
| 4483 |
+
a4483
|
| 4484 |
+
a4484
|
| 4485 |
+
a4485
|
| 4486 |
+
a4486
|
| 4487 |
+
a4487
|
| 4488 |
+
a4488
|
| 4489 |
+
a4489
|
| 4490 |
+
a4490
|
| 4491 |
+
a4491
|
| 4492 |
+
a4492
|
| 4493 |
+
a4493
|
| 4494 |
+
a4494
|
| 4495 |
+
a4495
|
| 4496 |
+
a4496
|
| 4497 |
+
a4497
|
| 4498 |
+
a4498
|
| 4499 |
+
a4499
|
| 4500 |
+
a4500
|
models/attention_fusion.py
ADDED
|
@@ -0,0 +1,108 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
import torch
|
| 2 |
+
from torch import nn
|
| 3 |
+
|
| 4 |
+
class LocalFusion(nn.Module):
|
| 5 |
+
def __init__(self, att_in_dim=3, num_categories=6, max_pool_ksize1=4, max_pool_ksize2=2, encoder_dims=[8, 16]):
|
| 6 |
+
super().__init__()
|
| 7 |
+
self.num_categories = num_categories
|
| 8 |
+
self.att_in_dim = att_in_dim
|
| 9 |
+
|
| 10 |
+
self.attention_fusion = nn.ModuleList([Self_Attn(in_dim=att_in_dim, max_pool_ksize1=max_pool_ksize1, max_pool_ksize2=max_pool_ksize2, encoder_dims=encoder_dims) for _ in range(num_categories)])
|
| 11 |
+
|
| 12 |
+
def forward(self, x, color_naming_probs=None, q=None):
|
| 13 |
+
|
| 14 |
+
# Using the average to compute the blending
|
| 15 |
+
if color_naming_probs is None:
|
| 16 |
+
# Using the same input tensor for query, key, and value
|
| 17 |
+
if q is None:
|
| 18 |
+
return torch.mean(torch.stack([att(x_color, q=x) for att, x_color in zip(self.attention_fusion, x)], dim=0))
|
| 19 |
+
else:
|
| 20 |
+
return torch.mean(torch.stack([att(x_color, q=q) for att, x_color in zip(self.attention_fusion, x)], dim=0))
|
| 21 |
+
|
| 22 |
+
# Using the color naming probabilities to compute the blending. Weighted average with color naming probs as
|
| 23 |
+
# weights.
|
| 24 |
+
else:
|
| 25 |
+
color_naming_probs = (color_naming_probs > 0.20).float()
|
| 26 |
+
color_naming_avg = torch.sum(color_naming_probs, dim=0).unsqueeze(1).repeat(1, 3, 1, 1)
|
| 27 |
+
color_naming_probs = color_naming_probs.unsqueeze(2).repeat(1, 1, 3, 1, 1)
|
| 28 |
+
|
| 29 |
+
# Using the same input tensor for query, key, and value
|
| 30 |
+
if q is None:
|
| 31 |
+
out = torch.stack([att(x_color, q=x) for att, x_color in zip(self.attention_fusion, x)], dim=0)
|
| 32 |
+
else:
|
| 33 |
+
out = torch.stack([att(x_color, q=q) for att, x_color in zip(self.attention_fusion, x)], dim=0)
|
| 34 |
+
|
| 35 |
+
out = torch.sum(out * color_naming_probs, dim=0) / color_naming_avg
|
| 36 |
+
return torch.clip(out, 0, 1)
|
| 37 |
+
|
| 38 |
+
class Self_Attn(nn.Module):
|
| 39 |
+
def __init__(self, in_dim, max_pool_ksize1=4, max_pool_ksize2=2, encoder_dims=[8, 16]):
|
| 40 |
+
super(Self_Attn, self).__init__()
|
| 41 |
+
self.chanel_in = in_dim
|
| 42 |
+
self.max_pool_ksize1 = max_pool_ksize1
|
| 43 |
+
self.max_pool_ksize2 = max_pool_ksize2
|
| 44 |
+
self.down_ratio = max_pool_ksize1 * max_pool_ksize2
|
| 45 |
+
|
| 46 |
+
self.query_conv = nn.Sequential(
|
| 47 |
+
nn.Conv2d(in_channels=in_dim, out_channels=encoder_dims[0], kernel_size=1),
|
| 48 |
+
nn.ReLU(),
|
| 49 |
+
nn.MaxPool2d(4, 4),
|
| 50 |
+
nn.Conv2d(in_channels=encoder_dims[0], out_channels=encoder_dims[1], kernel_size=1),
|
| 51 |
+
nn.ReLU(),
|
| 52 |
+
nn.MaxPool2d(2, 2))
|
| 53 |
+
|
| 54 |
+
self.key_conv = nn.Sequential(
|
| 55 |
+
nn.Conv2d(in_channels=in_dim, out_channels=encoder_dims[0], kernel_size=1),
|
| 56 |
+
nn.ReLU(),
|
| 57 |
+
nn.MaxPool2d(4, 4),
|
| 58 |
+
nn.Conv2d(in_channels=encoder_dims[0], out_channels=encoder_dims[1], kernel_size=1),
|
| 59 |
+
nn.ReLU(),
|
| 60 |
+
nn.MaxPool2d(2, 2))
|
| 61 |
+
|
| 62 |
+
self.value_conv = nn.Sequential(
|
| 63 |
+
nn.Conv2d(in_channels=in_dim, out_channels=encoder_dims[0], kernel_size=1),
|
| 64 |
+
nn.ReLU(),
|
| 65 |
+
nn.MaxPool2d(4, 4),
|
| 66 |
+
nn.Conv2d(in_channels=encoder_dims[0], out_channels=encoder_dims[1], kernel_size=1),
|
| 67 |
+
nn.ReLU(),
|
| 68 |
+
nn.MaxPool2d(2, 2))
|
| 69 |
+
|
| 70 |
+
self.upsample = nn.Sequential(
|
| 71 |
+
nn.Conv2d(in_channels=encoder_dims[1], out_channels=encoder_dims[0], kernel_size=1),
|
| 72 |
+
nn.ReLU(),
|
| 73 |
+
nn.UpsamplingNearest2d(scale_factor=4),
|
| 74 |
+
nn.Conv2d(in_channels=encoder_dims[0], out_channels=encoder_dims[0], kernel_size=1),
|
| 75 |
+
nn.ReLU(),
|
| 76 |
+
nn.Conv2d(in_channels=encoder_dims[0], out_channels=3, kernel_size=1),
|
| 77 |
+
nn.ReLU())
|
| 78 |
+
|
| 79 |
+
self.last_conv = nn.Conv2d(in_channels=3, out_channels=3, kernel_size=1)
|
| 80 |
+
|
| 81 |
+
self.gamma = nn.Parameter(torch.zeros(1))
|
| 82 |
+
|
| 83 |
+
self.max_pool = nn.MaxPool2d(2, 2)
|
| 84 |
+
self.softmax = nn.Softmax(dim=-1)
|
| 85 |
+
|
| 86 |
+
def forward(self, x, q=None):
|
| 87 |
+
|
| 88 |
+
if q is None:
|
| 89 |
+
q = x
|
| 90 |
+
|
| 91 |
+
m_batch_size, C, width, height = x.size()
|
| 92 |
+
proj_query = self.query_conv(q).view(m_batch_size, -1, int((width//self.down_ratio)*(height//self.down_ratio))).permute(0, 2, 1)
|
| 93 |
+
proj_key = self.key_conv(x).view(m_batch_size, -1, int((width//self.down_ratio)*(height//self.down_ratio)))
|
| 94 |
+
energy = torch.bmm(proj_query, proj_key)
|
| 95 |
+
attention = self.softmax(energy)
|
| 96 |
+
proj_value = self.value_conv(x).view(m_batch_size, -1, int((width//self.down_ratio)*(height//self.down_ratio)))
|
| 97 |
+
|
| 98 |
+
out = torch.bmm(proj_value, attention.permute(0, 2, 1))
|
| 99 |
+
out = out.view(m_batch_size, 16, int(width//self.down_ratio), int(height//self.down_ratio))
|
| 100 |
+
|
| 101 |
+
out = self.upsample(out)
|
| 102 |
+
upsampled_layer = nn.Upsample(size=x.size()[2:], mode='bilinear', align_corners=False)
|
| 103 |
+
out = upsampled_layer(out)
|
| 104 |
+
|
| 105 |
+
out = self.last_conv(out)
|
| 106 |
+
|
| 107 |
+
out = out + x
|
| 108 |
+
return out
|
models/backbone.py
ADDED
|
@@ -0,0 +1,234 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
"""
|
| 2 |
+
backbone.py - Contains the backbone of the model.
|
| 3 |
+
(It is based on LPIENet and CURL's backbone)
|
| 4 |
+
|
| 5 |
+
Perceptual Image Enhancement for Smartphone Real-Time Applications
|
| 6 |
+
https://github.com/mv-lab/AISP
|
| 7 |
+
|
| 8 |
+
CURL: Neural Curve Layers for Global Image Enhancement
|
| 9 |
+
https://github.com/sjmoran/CURL
|
| 10 |
+
|
| 11 |
+
David Serrano (dserrano@cvc.uab.cat)
|
| 12 |
+
May 2024
|
| 13 |
+
"""
|
| 14 |
+
import torch
|
| 15 |
+
import torch.nn as nn
|
| 16 |
+
import torch.nn.functional as F
|
| 17 |
+
from typing import List
|
| 18 |
+
|
| 19 |
+
|
| 20 |
+
class AttentionBlock(nn.Module):
|
| 21 |
+
def __init__(self, dim: int):
|
| 22 |
+
super(AttentionBlock, self).__init__()
|
| 23 |
+
self._spatial_attention_conv = nn.Conv2d(2, dim, kernel_size=3, padding=1)
|
| 24 |
+
|
| 25 |
+
# Channel attention MLP
|
| 26 |
+
self._channel_attention_conv0 = nn.Conv2d(1, dim, kernel_size=1, padding=0)
|
| 27 |
+
self._channel_attention_conv1 = nn.Conv2d(dim, dim, kernel_size=1, padding=0)
|
| 28 |
+
|
| 29 |
+
self._out_conv = nn.Conv2d(2 * dim, dim, kernel_size=1, padding=0)
|
| 30 |
+
|
| 31 |
+
def forward(self, x: torch.Tensor):
|
| 32 |
+
if len(x.shape) != 4:
|
| 33 |
+
raise ValueError(f"Expected [B, C, H, W] input, got {x.shape}.")
|
| 34 |
+
|
| 35 |
+
# Spatial attention
|
| 36 |
+
mean = torch.mean(x, dim=1, keepdim=True) # Mean/Max on C axis
|
| 37 |
+
max, _ = torch.max(x, dim=1, keepdim=True)
|
| 38 |
+
spatial_attention = torch.cat([mean, max], dim=1) # [B, 2, H, W]
|
| 39 |
+
spatial_attention = self._spatial_attention_conv(spatial_attention)
|
| 40 |
+
spatial_attention = torch.sigmoid(spatial_attention) * x
|
| 41 |
+
|
| 42 |
+
# NOTE: This differs from CBAM as it uses Channel pooling, not spatial pooling!
|
| 43 |
+
# In a way, this is 2x spatial attention
|
| 44 |
+
channel_attention = torch.relu(self._channel_attention_conv0(mean))
|
| 45 |
+
channel_attention = self._channel_attention_conv1(channel_attention)
|
| 46 |
+
channel_attention = torch.sigmoid(channel_attention) * x
|
| 47 |
+
|
| 48 |
+
attention = torch.cat([spatial_attention, channel_attention], dim=1) # [B, 2*dim, H, W]
|
| 49 |
+
attention = self._out_conv(attention)
|
| 50 |
+
return x + attention
|
| 51 |
+
|
| 52 |
+
|
| 53 |
+
class InverseBlock(nn.Module):
|
| 54 |
+
def __init__(self, input_channels: int, channels: int):
|
| 55 |
+
super(InverseBlock, self).__init__()
|
| 56 |
+
|
| 57 |
+
self._conv0 = nn.Conv2d(input_channels, channels, kernel_size=1)
|
| 58 |
+
self._dw_conv = nn.Conv2d(channels, channels, kernel_size=3, padding=1, groups=channels)
|
| 59 |
+
self._conv1 = nn.Conv2d(channels, channels, kernel_size=1)
|
| 60 |
+
self._conv2 = nn.Conv2d(input_channels, channels, kernel_size=1)
|
| 61 |
+
|
| 62 |
+
def forward(self, x: torch.Tensor):
|
| 63 |
+
features = self._conv0(x)
|
| 64 |
+
features = F.elu(self._dw_conv(features))
|
| 65 |
+
features = self._conv1(features)
|
| 66 |
+
|
| 67 |
+
x = torch.relu(self._conv2(x))
|
| 68 |
+
return x + features
|
| 69 |
+
|
| 70 |
+
|
| 71 |
+
class BaseBlock(nn.Module):
|
| 72 |
+
def __init__(self, channels: int):
|
| 73 |
+
super(BaseBlock, self).__init__()
|
| 74 |
+
|
| 75 |
+
self._conv0 = nn.Conv2d(channels, channels, kernel_size=1)
|
| 76 |
+
self._dw_conv = nn.Conv2d(channels, channels, kernel_size=3, padding=1, groups=channels)
|
| 77 |
+
self._conv1 = nn.Conv2d(channels, channels, kernel_size=1)
|
| 78 |
+
|
| 79 |
+
self._conv2 = nn.Conv2d(channels, channels, kernel_size=1)
|
| 80 |
+
self._conv3 = nn.Conv2d(channels, channels, kernel_size=1)
|
| 81 |
+
|
| 82 |
+
def forward(self, x: torch.Tensor):
|
| 83 |
+
features = self._conv0(x)
|
| 84 |
+
features = F.elu(self._dw_conv(features))
|
| 85 |
+
features = self._conv1(features)
|
| 86 |
+
x = x + features
|
| 87 |
+
|
| 88 |
+
features = F.elu(self._conv2(x))
|
| 89 |
+
features = self._conv3(features)
|
| 90 |
+
return x + features
|
| 91 |
+
|
| 92 |
+
|
| 93 |
+
class AttentionTail(nn.Module):
|
| 94 |
+
def __init__(self, channels: int):
|
| 95 |
+
super(AttentionTail, self).__init__()
|
| 96 |
+
|
| 97 |
+
self._conv0 = nn.Conv2d(channels, channels, kernel_size=7, padding=3)
|
| 98 |
+
self._conv1 = nn.Conv2d(channels, channels, kernel_size=5, padding=2)
|
| 99 |
+
self._conv2 = nn.Conv2d(channels, channels, kernel_size=3, padding=1)
|
| 100 |
+
|
| 101 |
+
def forward(self, x: torch.Tensor):
|
| 102 |
+
attention = torch.relu(self._conv0(x))
|
| 103 |
+
attention = torch.relu(self._conv1(attention))
|
| 104 |
+
attention = torch.sigmoid(self._conv2(attention))
|
| 105 |
+
return x * attention
|
| 106 |
+
|
| 107 |
+
class Flatten(nn.Module):
|
| 108 |
+
|
| 109 |
+
def forward(self, x):
|
| 110 |
+
"""Flatten a Tensor to a Vector
|
| 111 |
+
|
| 112 |
+
:param x: Tensor
|
| 113 |
+
:returns: 1D Tensor
|
| 114 |
+
:rtype: Tensor
|
| 115 |
+
|
| 116 |
+
"""
|
| 117 |
+
return x.view(x.size()[0], -1)
|
| 118 |
+
|
| 119 |
+
class ResidualConnection(nn.Module):
|
| 120 |
+
def __init__(self, in_channels):
|
| 121 |
+
super(ResidualConnection, self).__init__()
|
| 122 |
+
|
| 123 |
+
self.in_channels = in_channels
|
| 124 |
+
|
| 125 |
+
self.midnet2 = nn.Sequential(
|
| 126 |
+
nn.Conv2d(in_channels, 64, 3, 1, 2, 2),
|
| 127 |
+
nn.LeakyReLU(),
|
| 128 |
+
nn.Conv2d(64, 64, 3, 1, 2, 2),
|
| 129 |
+
nn.LeakyReLU()
|
| 130 |
+
)
|
| 131 |
+
|
| 132 |
+
self.midnet4 = nn.Sequential(
|
| 133 |
+
nn.Conv2d(in_channels, 64, 3, 1, 4, 4),
|
| 134 |
+
nn.LeakyReLU(),
|
| 135 |
+
nn.Conv2d(64, 64, 3, 1, 4, 4),
|
| 136 |
+
nn.LeakyReLU()
|
| 137 |
+
)
|
| 138 |
+
|
| 139 |
+
self.globnet = nn.Sequential(
|
| 140 |
+
nn.Conv2d(in_channels, 64, 3, 2, 1, 1),
|
| 141 |
+
nn.LeakyReLU(),
|
| 142 |
+
nn.MaxPool2d(kernel_size=3, stride=2, padding=1),
|
| 143 |
+
nn.Conv2d(64, 64, 3, 2, 1, 1),
|
| 144 |
+
nn.LeakyReLU(),
|
| 145 |
+
nn.MaxPool2d(kernel_size=3, stride=2, padding=1),
|
| 146 |
+
nn.Conv2d(64, 64, 3, 2, 1, 1),
|
| 147 |
+
nn.LeakyReLU(),
|
| 148 |
+
nn.AdaptiveAvgPool2d(1),
|
| 149 |
+
Flatten(),
|
| 150 |
+
nn.Dropout(0.5),
|
| 151 |
+
nn.Linear(64, 64)
|
| 152 |
+
)
|
| 153 |
+
|
| 154 |
+
self.conv_fuse = nn.Conv2d(in_channels=192+in_channels, out_channels=in_channels, kernel_size=1)
|
| 155 |
+
def forward(self, x):
|
| 156 |
+
|
| 157 |
+
x_midnet2 = self.midnet2(x)
|
| 158 |
+
x_midnet4 = self.midnet4(x)
|
| 159 |
+
x_global = self.globnet(x).unsqueeze(2).unsqueeze(3)
|
| 160 |
+
x_global = x_global.repeat(1, 1, x_midnet2.shape[2], x_midnet2.shape[3])
|
| 161 |
+
|
| 162 |
+
x_fuse = torch.cat((x, x_midnet2, x_midnet4, x_global), dim=1)
|
| 163 |
+
x_out = self.conv_fuse(x_fuse)
|
| 164 |
+
|
| 165 |
+
return x_out
|
| 166 |
+
|
| 167 |
+
class Backbone(nn.Module):
|
| 168 |
+
def __init__(self, input_channels: int, output_channels: int, encoder_dims: List[int], decoder_dims: List[int]):
|
| 169 |
+
super(Backbone, self).__init__()
|
| 170 |
+
|
| 171 |
+
if len(encoder_dims) != len(decoder_dims) + 1 or len(decoder_dims) < 1:
|
| 172 |
+
raise ValueError(f"Unexpected encoder and decoder dims: {encoder_dims}, {decoder_dims}.")
|
| 173 |
+
|
| 174 |
+
if input_channels != output_channels:
|
| 175 |
+
raise NotImplementedError()
|
| 176 |
+
|
| 177 |
+
encoders = []
|
| 178 |
+
for i, encoder_dim in enumerate(encoder_dims):
|
| 179 |
+
input_dim = input_channels if i == 0 else encoder_dims[i - 1]
|
| 180 |
+
encoders.append(
|
| 181 |
+
nn.Sequential(
|
| 182 |
+
nn.Conv2d(input_dim, encoder_dim, kernel_size=3, padding=1),
|
| 183 |
+
BaseBlock(encoder_dim),
|
| 184 |
+
BaseBlock(encoder_dim),
|
| 185 |
+
AttentionBlock(encoder_dim),
|
| 186 |
+
)
|
| 187 |
+
)
|
| 188 |
+
self._encoders = nn.ModuleList(encoders)
|
| 189 |
+
|
| 190 |
+
decoders = []
|
| 191 |
+
for i, decoder_dim in enumerate(decoder_dims):
|
| 192 |
+
input_dim = encoder_dims[-1] if i == 0 else decoder_dims[i - 1] + encoder_dims[-i - 1]
|
| 193 |
+
decoders.append(
|
| 194 |
+
nn.Sequential(
|
| 195 |
+
nn.Conv2d(input_dim, decoder_dim, kernel_size=3, padding=1),
|
| 196 |
+
BaseBlock(decoder_dim),
|
| 197 |
+
BaseBlock(decoder_dim),
|
| 198 |
+
AttentionBlock(decoder_dim),
|
| 199 |
+
)
|
| 200 |
+
)
|
| 201 |
+
self._decoders = nn.ModuleList(decoders)
|
| 202 |
+
|
| 203 |
+
self._inverse_bock = InverseBlock(encoder_dims[0] + decoder_dims[-1], output_channels)
|
| 204 |
+
self._attention_tail = AttentionTail(output_channels)
|
| 205 |
+
|
| 206 |
+
residual_connections = []
|
| 207 |
+
for i, decoder_dim in enumerate(encoder_dims):
|
| 208 |
+
residual_connections.append(
|
| 209 |
+
ResidualConnection(in_channels=decoder_dim)
|
| 210 |
+
)
|
| 211 |
+
self._residual_connections = nn.ModuleList(residual_connections)
|
| 212 |
+
def forward(self, x: torch.Tensor):
|
| 213 |
+
if len(x.shape) != 4:
|
| 214 |
+
raise ValueError(f"Expected [B, C, H, W] input, got {x.shape}.")
|
| 215 |
+
global_residual = x
|
| 216 |
+
|
| 217 |
+
encoder_outputs, residual_connections = [], []
|
| 218 |
+
for i, encoder in enumerate(self._encoders):
|
| 219 |
+
x = encoder(x)
|
| 220 |
+
if i != len(self._encoders) - 1:
|
| 221 |
+
encoder_outputs.append(x)
|
| 222 |
+
residual_connections.append(self._residual_connections[i](x))
|
| 223 |
+
x = F.max_pool2d(x, kernel_size=2)
|
| 224 |
+
|
| 225 |
+
encoder_outputs.reverse()
|
| 226 |
+
residual_connections.reverse()
|
| 227 |
+
for i, decoder in enumerate(self._decoders):
|
| 228 |
+
x = decoder(x)
|
| 229 |
+
x = nn.Upsample(size=encoder_outputs[i].shape[2:], mode='bilinear', align_corners=False)(x)
|
| 230 |
+
x = torch.cat([x, residual_connections[i]], dim=1)
|
| 231 |
+
|
| 232 |
+
x = self._inverse_bock(x)
|
| 233 |
+
x = self._attention_tail(x)
|
| 234 |
+
return torch.clip(x + global_residual, 0, 1)
|
models/bezier_control_point_estimator.py
ADDED
|
@@ -0,0 +1,90 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
"""
|
| 2 |
+
bezier_control_point_estimator.py - Contains the Bezier Control Point Estimator model.
|
| 3 |
+
The Bezier Control Point Estimator estimates the set of control points that define the Bezier curve for each color name.
|
| 4 |
+
|
| 5 |
+
David Serrano (dserrano@cvc.uab.cat)
|
| 6 |
+
May 2024
|
| 7 |
+
"""
|
| 8 |
+
|
| 9 |
+
import torch
|
| 10 |
+
from torch import nn
|
| 11 |
+
|
| 12 |
+
class ContextualFeatureExtractor(nn.Module):
|
| 13 |
+
def __init__(self):
|
| 14 |
+
super().__init__()
|
| 15 |
+
self.main = nn.Sequential(
|
| 16 |
+
nn.Conv2d(3, 8, 3, 1, 1),
|
| 17 |
+
nn.ReLU(),
|
| 18 |
+
nn.Conv2d(8, 16, 3, 1, 1),
|
| 19 |
+
nn.ReLU(),
|
| 20 |
+
nn.Conv2d(16, 32, 3, 1, 1),
|
| 21 |
+
nn.ReLU(),
|
| 22 |
+
nn.Dropout(0.2),
|
| 23 |
+
nn.Conv2d(32, 64, 3, 1, 1),
|
| 24 |
+
nn.ReLU())
|
| 25 |
+
|
| 26 |
+
def forward(self, x):
|
| 27 |
+
return self.main(x)
|
| 28 |
+
|
| 29 |
+
class BezierColorBranch(nn.Module):
|
| 30 |
+
def __init__(self, num_control_points=10):
|
| 31 |
+
super().__init__()
|
| 32 |
+
self.num_control_points = num_control_points # +1, (0, 0) point
|
| 33 |
+
self.color_branch = nn.Sequential(
|
| 34 |
+
nn.Conv2d(65, 64, 3, 1, 1),
|
| 35 |
+
nn.ReLU(),
|
| 36 |
+
nn.MaxPool2d(2, 2),
|
| 37 |
+
nn.Conv2d(64, 32, 3, 1, 1),
|
| 38 |
+
nn.ReLU(),
|
| 39 |
+
nn.MaxPool2d(2, 2),
|
| 40 |
+
nn.Conv2d(32, 32, 3, 1, 1),
|
| 41 |
+
nn.ReLU(),
|
| 42 |
+
nn.Conv2d(32, 3 * self.num_control_points, 3, 1, 1),
|
| 43 |
+
nn.AdaptiveAvgPool2d((1, 1)))
|
| 44 |
+
|
| 45 |
+
self.sigmoid = nn.Sigmoid()
|
| 46 |
+
|
| 47 |
+
def create_control_points(self, x):
|
| 48 |
+
x = torch.cumsum(torch.cat([torch.zeros_like(x[..., :1]), x], dim=-1), dim=-1)
|
| 49 |
+
x = torch.stack([x, torch.linspace(0, 1, steps=self.num_control_points+1).unsqueeze(0).repeat(x.shape[0], x.shape[1], 1).cuda()], dim=-1)
|
| 50 |
+
return x
|
| 51 |
+
|
| 52 |
+
def forward(self, x):
|
| 53 |
+
x = self.color_branch(x).view(x.size(0), 3, self.num_control_points)
|
| 54 |
+
x = self.sigmoid(x)
|
| 55 |
+
x = x / torch.sum(x, dim=2)[..., None]
|
| 56 |
+
x = self.create_control_points(x)
|
| 57 |
+
return x
|
| 58 |
+
|
| 59 |
+
class BCPE(nn.Module):
|
| 60 |
+
def __init__(self, num_categories=6, num_control_points=10):
|
| 61 |
+
super().__init__()
|
| 62 |
+
|
| 63 |
+
self.contextual_feature_extractor = ContextualFeatureExtractor()
|
| 64 |
+
self.color_branches = nn.ModuleList([BezierColorBranch(num_control_points) for _ in range(num_categories)])
|
| 65 |
+
|
| 66 |
+
def binomial_coefficient(self, n, k):
|
| 67 |
+
"""
|
| 68 |
+
Calculate the binomial coefficient (n choose k).
|
| 69 |
+
"""
|
| 70 |
+
if k < 0 or k > n:
|
| 71 |
+
return 0.0
|
| 72 |
+
result = 1.0
|
| 73 |
+
for i in range(min(k, n - k)):
|
| 74 |
+
result *= (n - i)
|
| 75 |
+
result //= (i + 1)
|
| 76 |
+
return result
|
| 77 |
+
|
| 78 |
+
def apply_cubic_bezier(self, x, control_points):
|
| 79 |
+
|
| 80 |
+
n = control_points.shape[2]
|
| 81 |
+
output = torch.zeros_like(x)
|
| 82 |
+
for j in range(n):
|
| 83 |
+
output += control_points[..., j, 0].view(control_points.shape[0], control_points.shape[1], 1, 1) * self.binomial_coefficient(n - 1, j) * (1 - x) ** (n - 1 - j) * x ** j
|
| 84 |
+
return output
|
| 85 |
+
|
| 86 |
+
def forward(self, x, cn_probs):
|
| 87 |
+
feat = self.contextual_feature_extractor(x)
|
| 88 |
+
bezier_control_points = [color_branch(torch.cat((feat, color_probs.unsqueeze(1)), dim=1).float()) for color_branch, color_probs in zip(self.color_branches, cn_probs)]
|
| 89 |
+
global_adjusted_images = torch.stack([self.apply_cubic_bezier(x, control_points) for control_points in bezier_control_points], dim=0)
|
| 90 |
+
return global_adjusted_images
|
models/color_naming.py
ADDED
|
@@ -0,0 +1,70 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
"""
|
| 2 |
+
color_naming.py - Contains the Joost van de Weijer et al. (2009) color naming model.
|
| 3 |
+
|
| 4 |
+
David Serrano (dserrano@cvc.uab.cat)
|
| 5 |
+
May 2024
|
| 6 |
+
"""
|
| 7 |
+
|
| 8 |
+
import os
|
| 9 |
+
import pathlib
|
| 10 |
+
from scipy.io import loadmat
|
| 11 |
+
import torch
|
| 12 |
+
from torch import tensor as to_tensor
|
| 13 |
+
from torchvision.transforms.functional import pil_to_tensor
|
| 14 |
+
|
| 15 |
+
class ColorNaming():
|
| 16 |
+
def __init__(self, matrix_path=os.path.join(str(pathlib.Path(__file__).parent.resolve()), "joost_color_naming.mat"),
|
| 17 |
+
num_categories=6,
|
| 18 |
+
device='cuda'):
|
| 19 |
+
""" Van de Weijer et al. (2009) Color Naming model python implementation.
|
| 20 |
+
Van De Weijer, J. et al. Learning color names for real-world applications. IEEE Transactions on Image Processing
|
| 21 |
+
The class is based on the MATLAB implementation by Van de Weijer et al. (2009) and it needs the w2c.mat original
|
| 22 |
+
file. The input RGB image is converted to a set (6 or 11) color naming probability maps.
|
| 23 |
+
|
| 24 |
+
If num_categories is 6: orange-brown-yellow, achromatic, pink-purple, red, green, blue.
|
| 25 |
+
If num_categories is 11: black, blue, brown, gray, green, orange, pink, purple, red, white, yellow.
|
| 26 |
+
"""
|
| 27 |
+
self.matrix = to_tensor(loadmat(matrix_path)['w2c']).to(device)
|
| 28 |
+
self.num_categories = num_categories
|
| 29 |
+
self.device = device
|
| 30 |
+
|
| 31 |
+
if num_categories == 6:
|
| 32 |
+
self.color_categories = [[2,5,10], [0,3,9], [6,7], [8], [4], [1]]
|
| 33 |
+
self.color_categories = [torch.tensor(x).to(device) for x in self.color_categories]
|
| 34 |
+
|
| 35 |
+
def __call__(self, input_tensor):
|
| 36 |
+
"""Converts an RGB image to a color naming image.
|
| 37 |
+
|
| 38 |
+
Args:
|
| 39 |
+
input_tensor: batch of RGB images (B x 3 x H x W)
|
| 40 |
+
|
| 41 |
+
Returns:
|
| 42 |
+
torch.tensor: Color naming image.
|
| 43 |
+
"""
|
| 44 |
+
# Reconvert image to [0-255] range
|
| 45 |
+
input_tensor = torch.clamp(input_tensor, 0, 1)
|
| 46 |
+
img = (input_tensor * 255).int()
|
| 47 |
+
|
| 48 |
+
index_tensor = torch.floor(
|
| 49 |
+
img[:, 0, ...].view(img.shape[0], -1) / 8).long() + 32 * torch.floor(
|
| 50 |
+
img[:, 1, ...].view(img.shape[0], -1) / 8).long() + 32 * 32 * torch.floor(
|
| 51 |
+
img[:, 2, ...].view(img.shape[0], -1) / 8).long()
|
| 52 |
+
|
| 53 |
+
prob_maps = []
|
| 54 |
+
for w2cM in self.matrix.permute(*torch.arange(self.matrix.ndim-1, -1, -1)):
|
| 55 |
+
out = w2cM[index_tensor].view(input_tensor.size(0), input_tensor.size(2), input_tensor.size(3))
|
| 56 |
+
prob_maps.append(out)
|
| 57 |
+
prob_maps = torch.stack(prob_maps, dim=0)
|
| 58 |
+
|
| 59 |
+
if self.num_categories == 11:
|
| 60 |
+
return prob_maps
|
| 61 |
+
|
| 62 |
+
elif self.num_categories == 6:
|
| 63 |
+
category_probs = [] # prob maps for each color category. [0, 1]
|
| 64 |
+
for category in self.color_categories:
|
| 65 |
+
cat_tensors = torch.index_select(prob_maps, 0, category).sum(dim=0)
|
| 66 |
+
category_probs.append(cat_tensors)
|
| 67 |
+
|
| 68 |
+
category_probs = torch.stack(category_probs, dim=0)
|
| 69 |
+
|
| 70 |
+
return category_probs
|
models/interactive_model.py
ADDED
|
@@ -0,0 +1,125 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
"""NamedCurves model with interactive functionality. This version builds upon model.py and bezier_control_point_estimator.py by incorporating additional parameters."""
|
| 2 |
+
|
| 3 |
+
from models.attention_fusion import LocalFusion
|
| 4 |
+
from models.color_naming import ColorNaming
|
| 5 |
+
from models.backbone import Backbone
|
| 6 |
+
from torch import nn
|
| 7 |
+
|
| 8 |
+
from PIL import Image
|
| 9 |
+
from torchvision.transforms import functional as TF
|
| 10 |
+
import torch
|
| 11 |
+
|
| 12 |
+
class NamedCurves(nn.Module):
|
| 13 |
+
def __init__(self, configs: dict):
|
| 14 |
+
super().__init__()
|
| 15 |
+
self.model_configs = configs
|
| 16 |
+
|
| 17 |
+
self.backbone = Backbone(**configs['backbone']['params'])
|
| 18 |
+
self.color_naming = ColorNaming(num_categories=configs['color_naming']['num_categories'])
|
| 19 |
+
self.bcpe = BCPE(**configs['bezier_control_points_estimator']['params'])
|
| 20 |
+
self.local_fusion = LocalFusion(**configs['local_fusion']['params'])
|
| 21 |
+
|
| 22 |
+
def forward(self, x, return_backbone=False, return_curves=False, control_points=None):
|
| 23 |
+
x_backbone = self.backbone(x)
|
| 24 |
+
cn_probs = self.color_naming(x_backbone)
|
| 25 |
+
|
| 26 |
+
if return_curves:
|
| 27 |
+
x_global, control_points = self.bcpe(x_backbone, cn_probs, return_control_points=return_curves, control_points=control_points)
|
| 28 |
+
else:
|
| 29 |
+
x_global = self.bcpe(x_backbone, cn_probs, control_points=control_points)
|
| 30 |
+
|
| 31 |
+
out = self.local_fusion(x_global, cn_probs, q=x_backbone)
|
| 32 |
+
|
| 33 |
+
if return_backbone:
|
| 34 |
+
return out, x_backbone
|
| 35 |
+
if return_curves:
|
| 36 |
+
return out, control_points
|
| 37 |
+
return out
|
| 38 |
+
|
| 39 |
+
class ContextualFeatureExtractor(nn.Module):
|
| 40 |
+
def __init__(self):
|
| 41 |
+
super().__init__()
|
| 42 |
+
self.main = nn.Sequential(
|
| 43 |
+
nn.Conv2d(3, 8, 3, 1, 1),
|
| 44 |
+
nn.ReLU(),
|
| 45 |
+
nn.Conv2d(8, 16, 3, 1, 1),
|
| 46 |
+
nn.ReLU(),
|
| 47 |
+
nn.Conv2d(16, 32, 3, 1, 1),
|
| 48 |
+
nn.ReLU(),
|
| 49 |
+
nn.Dropout(0.2),
|
| 50 |
+
nn.Conv2d(32, 64, 3, 1, 1),
|
| 51 |
+
nn.ReLU())
|
| 52 |
+
|
| 53 |
+
def forward(self, x):
|
| 54 |
+
return self.main(x)
|
| 55 |
+
|
| 56 |
+
class BezierColorBranch(nn.Module):
|
| 57 |
+
def __init__(self, num_control_points=10):
|
| 58 |
+
super().__init__()
|
| 59 |
+
self.num_control_points = num_control_points # +1, (0, 0) point
|
| 60 |
+
self.color_branch = nn.Sequential(
|
| 61 |
+
nn.Conv2d(65, 64, 3, 1, 1),
|
| 62 |
+
nn.ReLU(),
|
| 63 |
+
nn.MaxPool2d(2, 2),
|
| 64 |
+
nn.Conv2d(64, 32, 3, 1, 1),
|
| 65 |
+
nn.ReLU(),
|
| 66 |
+
nn.MaxPool2d(2, 2),
|
| 67 |
+
nn.Conv2d(32, 32, 3, 1, 1),
|
| 68 |
+
nn.ReLU(),
|
| 69 |
+
nn.Conv2d(32, 3 * self.num_control_points, 3, 1, 1),
|
| 70 |
+
nn.AdaptiveAvgPool2d((1, 1)))
|
| 71 |
+
|
| 72 |
+
self.sigmoid = nn.Sigmoid()
|
| 73 |
+
|
| 74 |
+
def create_control_points(self, x):
|
| 75 |
+
x = torch.cumsum(torch.cat([torch.zeros_like(x[..., :1]), x], dim=-1), dim=-1)
|
| 76 |
+
x = torch.stack([x, torch.linspace(0, 1, steps=self.num_control_points+1).unsqueeze(0).repeat(x.shape[0], x.shape[1], 1).cuda()], dim=-1)
|
| 77 |
+
return x
|
| 78 |
+
|
| 79 |
+
def forward(self, x):
|
| 80 |
+
x = self.color_branch(x).view(x.size(0), 3, self.num_control_points)
|
| 81 |
+
x = self.sigmoid(x)
|
| 82 |
+
x = x / torch.sum(x, dim=2)[..., None]
|
| 83 |
+
x = self.create_control_points(x)
|
| 84 |
+
return x
|
| 85 |
+
|
| 86 |
+
class BCPE(nn.Module):
|
| 87 |
+
def __init__(self, num_categories=6, num_control_points=10):
|
| 88 |
+
super().__init__()
|
| 89 |
+
|
| 90 |
+
self.contextual_feature_extractor = ContextualFeatureExtractor()
|
| 91 |
+
self.color_branches = nn.ModuleList([BezierColorBranch(num_control_points) for _ in range(num_categories)])
|
| 92 |
+
|
| 93 |
+
def binomial_coefficient(self, n, k):
|
| 94 |
+
"""
|
| 95 |
+
Calculate the binomial coefficient (n choose k).
|
| 96 |
+
"""
|
| 97 |
+
if k < 0 or k > n:
|
| 98 |
+
return 0.0
|
| 99 |
+
result = 1.0
|
| 100 |
+
for i in range(min(k, n - k)):
|
| 101 |
+
result *= (n - i)
|
| 102 |
+
result //= (i + 1)
|
| 103 |
+
return result
|
| 104 |
+
|
| 105 |
+
def apply_cubic_bezier(self, x, control_points):
|
| 106 |
+
|
| 107 |
+
n = control_points.shape[2]
|
| 108 |
+
output = torch.zeros_like(x)
|
| 109 |
+
for j in range(n):
|
| 110 |
+
output += control_points[..., j, 0].view(control_points.shape[0], control_points.shape[1], 1, 1) * self.binomial_coefficient(n - 1, j) * (1 - x) ** (n - 1 - j) * x ** j
|
| 111 |
+
return output
|
| 112 |
+
|
| 113 |
+
def forward(self, x, cn_probs, return_control_points=False, control_points=None):
|
| 114 |
+
feat = self.contextual_feature_extractor(x)
|
| 115 |
+
bezier_control_points = [color_branch(torch.cat((feat, color_probs.unsqueeze(1)), dim=1).float()) for color_branch, color_probs in zip(self.color_branches, cn_probs)]
|
| 116 |
+
|
| 117 |
+
if control_points is not None:
|
| 118 |
+
bezier_control_points = control_points
|
| 119 |
+
|
| 120 |
+
global_adjusted_images = torch.stack([self.apply_cubic_bezier(x, control_points) for control_points in bezier_control_points], dim=0)
|
| 121 |
+
|
| 122 |
+
if return_control_points:
|
| 123 |
+
return global_adjusted_images, bezier_control_points
|
| 124 |
+
|
| 125 |
+
return global_adjusted_images
|
models/joost_color_naming.mat
ADDED
|
@@ -0,0 +1,3 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
version https://git-lfs.github.com/spec/v1
|
| 2 |
+
oid sha256:97b1f0ecd0fbecd122de319eacf3b5e23293defb06c40aa37a0446fb11d9cf45
|
| 3 |
+
size 2734783
|
models/model.py
ADDED
|
@@ -0,0 +1,28 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
from models.attention_fusion import LocalFusion
|
| 2 |
+
from models.bezier_control_point_estimator import BCPE
|
| 3 |
+
from models.color_naming import ColorNaming
|
| 4 |
+
from models.backbone import Backbone
|
| 5 |
+
from torch import nn
|
| 6 |
+
|
| 7 |
+
from PIL import Image
|
| 8 |
+
from torchvision.transforms import functional as TF
|
| 9 |
+
import torch
|
| 10 |
+
|
| 11 |
+
class NamedCurves(nn.Module):
|
| 12 |
+
def __init__(self, configs: dict):
|
| 13 |
+
super().__init__()
|
| 14 |
+
self.model_configs = configs
|
| 15 |
+
|
| 16 |
+
self.backbone = Backbone(**configs['backbone']['params'])
|
| 17 |
+
self.color_naming = ColorNaming(num_categories=configs['color_naming']['num_categories'])
|
| 18 |
+
self.bcpe = BCPE(**configs['bezier_control_points_estimator']['params'])
|
| 19 |
+
self.local_fusion = LocalFusion(**configs['local_fusion']['params'])
|
| 20 |
+
|
| 21 |
+
def forward(self, x, return_backbone=False):
|
| 22 |
+
x_backbone = self.backbone(x)
|
| 23 |
+
cn_probs = self.color_naming(x_backbone)
|
| 24 |
+
x_global = self.bcpe(x_backbone, cn_probs)
|
| 25 |
+
out = self.local_fusion(x_global, cn_probs, q=x_backbone)
|
| 26 |
+
if return_backbone:
|
| 27 |
+
return out, x_backbone
|
| 28 |
+
return out
|
output/a4957-input.png
ADDED

|
requirements.txt
ADDED
|
@@ -0,0 +1,33 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
antlr4-python3-runtime
|
| 2 |
+
certifi
|
| 3 |
+
charset-normalizer
|
| 4 |
+
contourpy
|
| 5 |
+
cycler
|
| 6 |
+
fonttools
|
| 7 |
+
idna
|
| 8 |
+
imageio
|
| 9 |
+
importlib_resources
|
| 10 |
+
kiwisolver
|
| 11 |
+
lazy_loader
|
| 12 |
+
lightning-utilities
|
| 13 |
+
lpips==
|
| 14 |
+
matplotlib
|
| 15 |
+
networkx
|
| 16 |
+
numpy
|
| 17 |
+
omegaconf
|
| 18 |
+
packaging
|
| 19 |
+
pillow
|
| 20 |
+
pyparsing
|
| 21 |
+
python-dateutil
|
| 22 |
+
PyWavelets
|
| 23 |
+
PyYAML
|
| 24 |
+
requests
|
| 25 |
+
scikit-image
|
| 26 |
+
scipy
|
| 27 |
+
six
|
| 28 |
+
tifffile
|
| 29 |
+
torchmetrics
|
| 30 |
+
tqdm
|
| 31 |
+
typing_extensions
|
| 32 |
+
urllib3
|
| 33 |
+
zipp
|
scripts/download_checkpoints.sh
ADDED
|
@@ -0,0 +1,9 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
#!/bin/bash
|
| 2 |
+
|
| 3 |
+
mkdir pretrained
|
| 4 |
+
wget https://github.com/davidserra9/namedcurves/releases/download/v1.0/mit5k_dpe_psnr_24.91.pth -P pretrained
|
| 5 |
+
wget https://github.com/davidserra9/namedcurves/releases/download/v1.0/mit5k_uegan_psnr_25.59.pth -P pretrained
|
| 6 |
+
wget https://github.com/davidserra9/namedcurves/releases/download/v1.0/ppr10k_a_psnr_26.81.pth -P pretrained
|
| 7 |
+
wget https://github.com/davidserra9/namedcurves/releases/download/v1.0/ppr10k_b_psnr_25.91.pth -P pretrained
|
| 8 |
+
wget https://github.com/davidserra9/namedcurves/releases/download/v1.0/ppr10k_c_psnr_25.69.pth -P pretrained
|
| 9 |
+
|
scripts/generate_naming_maps.py
ADDED
|
@@ -0,0 +1,29 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
import torch
|
| 2 |
+
import argparse
|
| 3 |
+
import os.path
|
| 4 |
+
from PIL import Image
|
| 5 |
+
from models.color_naming import ColorNaming
|
| 6 |
+
from torchvision.transforms import functional as TF
|
| 7 |
+
|
| 8 |
+
def parse_args():
|
| 9 |
+
parser = argparse.ArgumentParser()
|
| 10 |
+
parser.add_argument('--num_categories', type=int, default=6)
|
| 11 |
+
parser.add_argument('--image_path', type=str, default='/home/dserrano/Documents/datasets/FiveK-DPE/input/a0001-jmac_DSC1459.png')
|
| 12 |
+
parser.add_argument('--output_path', type=str)
|
| 13 |
+
return parser.parse_args()
|
| 14 |
+
|
| 15 |
+
if __name__ == "__main__":
|
| 16 |
+
args = parse_args()
|
| 17 |
+
color_naming = ColorNaming(num_categories=args.num_categories)
|
| 18 |
+
|
| 19 |
+
if os.path.isfile(args.image_path):
|
| 20 |
+
image_tensor = TF.pil_to_tensor(Image.open(args.image_path).convert('RGB')).unsqueeze(0)
|
| 21 |
+
cn_probs = color_naming(image_tensor).float().repeat(1, 3, 1, 1).cpu()
|
| 22 |
+
output_images = (1 - cn_probs) * 255 * torch.ones_like(image_tensor).repeat(args.num_categories, 1, 1, 1) + cn_probs * image_tensor.repeat(args.num_categories, 1, 1, 1)
|
| 23 |
+
|
| 24 |
+
import matplotlib.pyplot as plt
|
| 25 |
+
fig = plt.subplots(1, args.num_categories, figsize=(20, 20))
|
| 26 |
+
for i in range(args.num_categories):
|
| 27 |
+
plt.subplot(1, args.num_categories, i+1)
|
| 28 |
+
plt.imshow(output_images[i].permute(1, 2, 0).numpy().astype('uint8'))
|
| 29 |
+
plt.show()
|
test.py
ADDED
|
@@ -0,0 +1,41 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
import argparse
|
| 2 |
+
from models.model import NamedCurves
|
| 3 |
+
import torch
|
| 4 |
+
import os
|
| 5 |
+
from omegaconf import OmegaConf
|
| 6 |
+
from glob import glob
|
| 7 |
+
from PIL import Image
|
| 8 |
+
from torchvision.transforms import functional as TF
|
| 9 |
+
|
| 10 |
+
def parse_args():
|
| 11 |
+
parser = argparse.ArgumentParser()
|
| 12 |
+
parser.add_argument('--input_path', type=str, default='assets/a4957-input.png')
|
| 13 |
+
parser.add_argument('--output_path', type=str, default='output/')
|
| 14 |
+
parser.add_argument('--model_path', type=str, default='/home/dserrano/Workspace/Color-Naming-Image-Enhancement/pretrained/mit5k_uegan_psnr_25.59.pth')
|
| 15 |
+
parser.add_argument('--config_path', type=str, default='configs/mit5k_dpe_config.yaml')
|
| 16 |
+
return parser.parse_args()
|
| 17 |
+
|
| 18 |
+
def main():
|
| 19 |
+
args = parse_args()
|
| 20 |
+
config = OmegaConf.load(args.config_path)
|
| 21 |
+
model = NamedCurves(config.model).cuda()
|
| 22 |
+
model.load_state_dict(torch.load(args.model_path)["model_state_dict"])
|
| 23 |
+
|
| 24 |
+
if not os.path.exists(args.output_path):
|
| 25 |
+
os.makedirs(args.output_path)
|
| 26 |
+
|
| 27 |
+
#check if input_path is a folder
|
| 28 |
+
if os.path.isdir(args.input_path):
|
| 29 |
+
input_paths = glob(sorted(args.input_path + '/*'))
|
| 30 |
+
|
| 31 |
+
else:
|
| 32 |
+
input_paths = [args.input_path]
|
| 33 |
+
|
| 34 |
+
for input_path in input_paths:
|
| 35 |
+
input_tensor = TF.to_tensor(Image.open(input_path)).unsqueeze(0)
|
| 36 |
+
output = model(input_tensor.cuda())
|
| 37 |
+
output = TF.to_pil_image(output[0].cpu())
|
| 38 |
+
output.save(os.path.join(args.output_path, os.path.basename(input_path)))
|
| 39 |
+
|
| 40 |
+
if __name__ == '__main__':
|
| 41 |
+
main()
|
train.py
ADDED
|
@@ -0,0 +1,73 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
import torch
|
| 2 |
+
import datetime
|
| 3 |
+
import os
|
| 4 |
+
import logging
|
| 5 |
+
|
| 6 |
+
import omegaconf
|
| 7 |
+
|
| 8 |
+
from utils.logger import prepare_logging
|
| 9 |
+
from torch.utils.data import DataLoader
|
| 10 |
+
from data.datasets import get_datasets
|
| 11 |
+
from models.model import NamingEnhancementModel
|
| 12 |
+
from utils.setup_optim_scheduler import get_optimizer_scheduler
|
| 13 |
+
from utils.evaluator import Evaluator
|
| 14 |
+
from utils.setup_criterion import get_criterion
|
| 15 |
+
from utils.trainer import Trainer
|
| 16 |
+
|
| 17 |
+
|
| 18 |
+
def main(config: omegaconf.DictConfig):
|
| 19 |
+
|
| 20 |
+
os.environ["CUDA_VISIBLE_DEVICES"] = str(config.train.cuda_visible_device)
|
| 21 |
+
save_path = prepare_logging()
|
| 22 |
+
|
| 23 |
+
logging.info(f"Starting training at {datetime.datetime.now().strftime('%Y-%m-%d %H:%M:%S')}")
|
| 24 |
+
logging.info(f"Saving logs to {save_path}")
|
| 25 |
+
logging.info(f"Config file: {OmegaConf.to_yaml(config)}")
|
| 26 |
+
|
| 27 |
+
train_dataset, valid_dataset, test_dataset = get_datasets(config.data)
|
| 28 |
+
|
| 29 |
+
msg = f"Training with {len(train_dataset)} image pairs"
|
| 30 |
+
if valid_dataset is not None:
|
| 31 |
+
msg += f", validating with {len(valid_dataset)} image pairs"
|
| 32 |
+
msg += f" and testing with {len(test_dataset)} image pairs."
|
| 33 |
+
logging.info(msg)
|
| 34 |
+
|
| 35 |
+
train_loader = DataLoader(train_dataset, batch_size=config.train.batch_size, shuffle=True)
|
| 36 |
+
if valid_dataset is not None:
|
| 37 |
+
valid_loader = DataLoader(valid_dataset, batch_size=1, shuffle=False)
|
| 38 |
+
else:
|
| 39 |
+
valid_loader = None
|
| 40 |
+
test_loader = DataLoader(test_dataset, batch_size=1, shuffle=False)
|
| 41 |
+
|
| 42 |
+
model = NamingEnhancementModel(config.model)
|
| 43 |
+
if config.model.ckpt_path is not None:
|
| 44 |
+
model.load_state_dict(torch.load(config.model.ckpt_path)["model_state_dict"])
|
| 45 |
+
model.cuda()
|
| 46 |
+
|
| 47 |
+
criterion = get_criterion(config.train.criterion)
|
| 48 |
+
|
| 49 |
+
optimizer, scheduler = get_optimizer_scheduler(model,
|
| 50 |
+
config.train.optimizer,
|
| 51 |
+
config.train.scheduler if "scheduler" in config.train else None)
|
| 52 |
+
|
| 53 |
+
if valid_loader is not None:
|
| 54 |
+
valid_evaluator = Evaluator(valid_loader, config.eval.metrics, 'valid', save_path, config.eval.metric_to_save)
|
| 55 |
+
else:
|
| 56 |
+
valid_evaluator = None
|
| 57 |
+
|
| 58 |
+
test_evaluator = Evaluator(test_loader, config.eval.metrics, 'test', save_path, config.eval.metric_to_save)
|
| 59 |
+
|
| 60 |
+
|
| 61 |
+
trainer = Trainer(model, optimizer, criterion, scheduler, train_loader, valid_evaluator, test_evaluator, config.train, config.eval)
|
| 62 |
+
trainer.train()
|
| 63 |
+
|
| 64 |
+
if __name__ == "__main__":
|
| 65 |
+
from omegaconf import OmegaConf
|
| 66 |
+
import argparse
|
| 67 |
+
|
| 68 |
+
parser = argparse.ArgumentParser()
|
| 69 |
+
parser.add_argument('--config', type=str, default='configs/mit5k_dpe_config.yaml')
|
| 70 |
+
args = parser.parse_args()
|
| 71 |
+
|
| 72 |
+
config = OmegaConf.load(args.config)
|
| 73 |
+
main(config)
|
utils/deltaE.py
ADDED
|
@@ -0,0 +1,125 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
from skimage import color
|
| 2 |
+
import numpy as np
|
| 3 |
+
import torch
|
| 4 |
+
|
| 5 |
+
class deltaEab():
|
| 6 |
+
def __init__(self, color_chart_area=0):
|
| 7 |
+
super().__init__()
|
| 8 |
+
self.color_chart_area = color_chart_area
|
| 9 |
+
|
| 10 |
+
def __call__(self, img1, img2):
|
| 11 |
+
""" Compute the deltaE76 between two numpy RGB images
|
| 12 |
+
From M. Afifi: https://github.com/mahmoudnafifi/WB_sRGB/blob/master/WB_sRGB_Python/evaluation/calc_deltaE.py
|
| 13 |
+
:param img1: numpy RGB image or pytorch tensor
|
| 14 |
+
:param img2: numpy RGB image or pytocrh tensor
|
| 15 |
+
:return: deltaE76
|
| 16 |
+
"""
|
| 17 |
+
|
| 18 |
+
if type(img1) == torch.Tensor:
|
| 19 |
+
assert img1.shape[0] == 1
|
| 20 |
+
img1 = img1.squeeze().permute(1, 2, 0).cpu().numpy()
|
| 21 |
+
|
| 22 |
+
if type(img2) == torch.Tensor:
|
| 23 |
+
assert img2.shape[0] == 1
|
| 24 |
+
img2 = img2.squeeze().permute(1, 2, 0).cpu().numpy()
|
| 25 |
+
|
| 26 |
+
# Convert to Lab
|
| 27 |
+
img1 = color.rgb2lab(img1)
|
| 28 |
+
img2 = color.rgb2lab(img2)
|
| 29 |
+
|
| 30 |
+
# reshape to 1D array
|
| 31 |
+
img1 = img1.reshape(-1, 3).astype(np.float32)
|
| 32 |
+
img2 = img2.reshape(-1, 3).astype(np.float32)
|
| 33 |
+
|
| 34 |
+
# compute deltaE76
|
| 35 |
+
de76 = np.sqrt(np.sum(np.power(img1 - img2, 2), 1))
|
| 36 |
+
|
| 37 |
+
return sum(de76) / (np.shape(de76)[0] - self.color_chart_area)
|
| 38 |
+
|
| 39 |
+
|
| 40 |
+
class deltaE00():
|
| 41 |
+
def __init__(self, color_chart_area=0):
|
| 42 |
+
super().__init__()
|
| 43 |
+
self.color_chart_area = color_chart_area
|
| 44 |
+
self.kl = 1
|
| 45 |
+
self.kc = 1
|
| 46 |
+
self.kh = 1
|
| 47 |
+
|
| 48 |
+
def __call__(self, img1, img2):
|
| 49 |
+
""" Compute the deltaE00 between two numpy RGB images
|
| 50 |
+
From M. Afifi: https://github.com/mahmoudnafifi/WB_sRGB/blob/master/WB_sRGB_Python/evaluation/calc_deltaE2000.py
|
| 51 |
+
:param img1: numpy RGB image or pytocrh tensor
|
| 52 |
+
:param img2: numpy RGB image or pytocrh tensor
|
| 53 |
+
:return: deltaE00
|
| 54 |
+
"""
|
| 55 |
+
|
| 56 |
+
if type(img1) == torch.Tensor:
|
| 57 |
+
assert img1.shape[0] == 1
|
| 58 |
+
img1 = img1.squeeze().permute(1, 2, 0).cpu().numpy()
|
| 59 |
+
|
| 60 |
+
if type(img2) == torch.Tensor:
|
| 61 |
+
assert img2.shape[0] == 1
|
| 62 |
+
img2 = img2.squeeze().permute(1, 2, 0).cpu().numpy()
|
| 63 |
+
|
| 64 |
+
# Convert to Lab
|
| 65 |
+
img1 = color.rgb2lab(img1)
|
| 66 |
+
img2 = color.rgb2lab(img2)
|
| 67 |
+
|
| 68 |
+
# reshape to 1D array
|
| 69 |
+
img1 = img1.reshape(-1, 3).astype(np.float32)
|
| 70 |
+
img2 = img2.reshape(-1, 3).astype(np.float32)
|
| 71 |
+
|
| 72 |
+
# compute deltaE00
|
| 73 |
+
Lstd = np.transpose(img1[:, 0])
|
| 74 |
+
astd = np.transpose(img1[:, 1])
|
| 75 |
+
bstd = np.transpose(img1[:, 2])
|
| 76 |
+
Cabstd = np.sqrt(np.power(astd, 2) + np.power(bstd, 2))
|
| 77 |
+
Lsample = np.transpose(img2[:, 0])
|
| 78 |
+
asample = np.transpose(img2[:, 1])
|
| 79 |
+
bsample = np.transpose(img2[:, 2])
|
| 80 |
+
Cabsample = np.sqrt(np.power(asample, 2) + np.power(bsample, 2))
|
| 81 |
+
Cabarithmean = (Cabstd + Cabsample) / 2
|
| 82 |
+
G = 0.5 * (1 - np.sqrt((np.power(Cabarithmean, 7)) / (np.power(
|
| 83 |
+
Cabarithmean, 7) + np.power(25, 7))))
|
| 84 |
+
apstd = (1 + G) * astd
|
| 85 |
+
apsample = (1 + G) * asample
|
| 86 |
+
Cpsample = np.sqrt(np.power(apsample, 2) + np.power(bsample, 2))
|
| 87 |
+
Cpstd = np.sqrt(np.power(apstd, 2) + np.power(bstd, 2))
|
| 88 |
+
Cpprod = (Cpsample * Cpstd)
|
| 89 |
+
zcidx = np.argwhere(Cpprod == 0)
|
| 90 |
+
hpstd = np.arctan2(bstd, apstd)
|
| 91 |
+
hpstd[np.argwhere((np.abs(apstd) + np.abs(bstd)) == 0)] = 0
|
| 92 |
+
hpsample = np.arctan2(bsample, apsample)
|
| 93 |
+
hpsample = hpsample + 2 * np.pi * (hpsample < 0)
|
| 94 |
+
hpsample[np.argwhere((np.abs(apsample) + np.abs(bsample)) == 0)] = 0
|
| 95 |
+
dL = (Lsample - Lstd)
|
| 96 |
+
dC = (Cpsample - Cpstd)
|
| 97 |
+
dhp = (hpsample - hpstd)
|
| 98 |
+
dhp = dhp - 2 * np.pi * (dhp > np.pi)
|
| 99 |
+
dhp = dhp + 2 * np.pi * (dhp < (-np.pi))
|
| 100 |
+
dhp[zcidx] = 0
|
| 101 |
+
dH = 2 * np.sqrt(Cpprod) * np.sin(dhp / 2)
|
| 102 |
+
Lp = (Lsample + Lstd) / 2
|
| 103 |
+
Cp = (Cpstd + Cpsample) / 2
|
| 104 |
+
hp = (hpstd + hpsample) / 2
|
| 105 |
+
hp = hp - (np.abs(hpstd - hpsample) > np.pi) * np.pi
|
| 106 |
+
hp = hp + (hp < 0) * 2 * np.pi
|
| 107 |
+
hp[zcidx] = hpsample[zcidx] + hpstd[zcidx]
|
| 108 |
+
Lpm502 = np.power((Lp - 50), 2)
|
| 109 |
+
Sl = 1 + 0.015 * Lpm502 / np.sqrt(20 + Lpm502)
|
| 110 |
+
Sc = 1 + 0.045 * Cp
|
| 111 |
+
T = 1 - 0.17 * np.cos(hp - np.pi / 6) + 0.24 * np.cos(2 * hp) + \
|
| 112 |
+
0.32 * np.cos(3 * hp + np.pi / 30) \
|
| 113 |
+
- 0.20 * np.cos(4 * hp - 63 * np.pi / 180)
|
| 114 |
+
Sh = 1 + 0.015 * Cp * T
|
| 115 |
+
delthetarad = (30 * np.pi / 180) * np.exp(
|
| 116 |
+
- np.power((180 / np.pi * hp - 275) / 25, 2))
|
| 117 |
+
Rc = 2 * np.sqrt((np.power(Cp, 7)) / (np.power(Cp, 7) + np.power(25, 7)))
|
| 118 |
+
RT = - np.sin(2 * delthetarad) * Rc
|
| 119 |
+
klSl = self.kl * Sl
|
| 120 |
+
kcSc = self.kc * Sc
|
| 121 |
+
khSh = self.kh * Sh
|
| 122 |
+
de00 = np.sqrt(np.power((dL / klSl), 2) + np.power((dC / kcSc), 2) +
|
| 123 |
+
np.power((dH / khSh), 2) + RT * (dC / kcSc) * (dH / khSh))
|
| 124 |
+
|
| 125 |
+
return np.sum(de00) / (np.shape(de00)[0] - self.color_chart_area)
|
utils/evaluator.py
ADDED
|
@@ -0,0 +1,69 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
import torch
|
| 2 |
+
import logging
|
| 3 |
+
from torchmetrics import PeakSignalNoiseRatio as PSNR
|
| 4 |
+
from torchmetrics import StructuralSimilarityIndexMeasure as SSIM
|
| 5 |
+
from lpips import LPIPS
|
| 6 |
+
from utils.deltaE import deltaEab, deltaE00
|
| 7 |
+
|
| 8 |
+
class Evaluator():
|
| 9 |
+
def __init__(self, dataloader, metrics, split_name, log_dirpath, best_metric):
|
| 10 |
+
self.dataloader = dataloader
|
| 11 |
+
self._create_metrics(metrics)
|
| 12 |
+
self.split_name = split_name
|
| 13 |
+
self.log_dirpath = log_dirpath
|
| 14 |
+
self.best_metric = best_metric
|
| 15 |
+
self.best_value = 0
|
| 16 |
+
|
| 17 |
+
def _create_metrics(self, metrics):
|
| 18 |
+
self.metrics = {}
|
| 19 |
+
self.cumulative_values = {}
|
| 20 |
+
for metric in metrics:
|
| 21 |
+
if metric.type == 'PSNR':
|
| 22 |
+
self.metrics['PSNR'] = PSNR(**metric.params).cuda()
|
| 23 |
+
self.cumulative_values['PSNR'] = 0
|
| 24 |
+
elif metric.type == 'SSIM':
|
| 25 |
+
self.metrics['SSIM'] = SSIM(**metric.params).cuda()
|
| 26 |
+
self.cumulative_values['SSIM'] = 0
|
| 27 |
+
elif metric.type == 'LPIPS':
|
| 28 |
+
self.metrics['LPIPS'] = LPIPS(**metric.params).cuda()
|
| 29 |
+
self.cumulative_values['LPIPS'] = 0
|
| 30 |
+
elif metric.type == 'deltaEab':
|
| 31 |
+
self.metrics['deltaEab'] = deltaEab()
|
| 32 |
+
self.cumulative_values['deltaEab'] = 0
|
| 33 |
+
elif metric.type == 'deltaE00':
|
| 34 |
+
self.metrics['deltaE00'] = deltaE00()
|
| 35 |
+
self.cumulative_values['deltaE00'] = 0
|
| 36 |
+
else:
|
| 37 |
+
raise NotImplementedError(f"Metric {metric.type} not implemented")
|
| 38 |
+
|
| 39 |
+
def _compute_metrics(self, input_image, target_image):
|
| 40 |
+
for name, metric in self.metrics.items():
|
| 41 |
+
self.cumulative_values[name] += metric(input_image, target_image)
|
| 42 |
+
|
| 43 |
+
def _compute_average_metrics(self):
|
| 44 |
+
avg_metrics = {}
|
| 45 |
+
for name, value in self.cumulative_values.items():
|
| 46 |
+
avg_metrics[name] = float(value / len(self.dataloader))
|
| 47 |
+
return avg_metrics
|
| 48 |
+
|
| 49 |
+
def _reset_metrics(self):
|
| 50 |
+
for metric in self.metrics:
|
| 51 |
+
self.cumulative_values[metric] = 0
|
| 52 |
+
|
| 53 |
+
def __call__(self, model, save_results=True):
|
| 54 |
+
model.eval()
|
| 55 |
+
self._reset_metrics()
|
| 56 |
+
with torch.no_grad():
|
| 57 |
+
for data in self.dataloader:
|
| 58 |
+
input_image, target_image, name = data['input_image'], data['target_image'], data['name']
|
| 59 |
+
|
| 60 |
+
self._compute_metrics(input_image.cuda(), target_image.cuda())
|
| 61 |
+
|
| 62 |
+
avg_metrics = self._compute_average_metrics()
|
| 63 |
+
logging.info(f"{self.split_name} metrics: " + ", ".join([f'{key}: {value:.4f}' for key, value in avg_metrics.items()]))
|
| 64 |
+
|
| 65 |
+
if (avg_metrics[self.best_metric] > self.best_value) and save_results:
|
| 66 |
+
self.best_value = avg_metrics[self.best_metric]
|
| 67 |
+
torch.save({**{'model_state_dict': model.state_dict()}, **avg_metrics},
|
| 68 |
+
f"{self.log_dirpath}/{self.split_name}_best_model.pth")
|
| 69 |
+
logging.info(f"New best model saved at {self.log_dirpath}/{self.split_name}_best_model.pth")
|
utils/logger.py
ADDED
|
@@ -0,0 +1,21 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
import logging
|
| 2 |
+
import os
|
| 3 |
+
import datetime
|
| 4 |
+
|
| 5 |
+
def prepare_logging():
|
| 6 |
+
save_path = os.path.join(os.path.dirname(os.path.dirname(os.path.abspath(__file__))), "logs")
|
| 7 |
+
if not os.path.exists(save_path):
|
| 8 |
+
os.makedirs(save_path)
|
| 9 |
+
|
| 10 |
+
timestamp = datetime.datetime.now().strftime('%Y%m%d_%H%M%S')
|
| 11 |
+
log_dirpath = "log_" + timestamp
|
| 12 |
+
save_path = os.path.join(save_path, log_dirpath)
|
| 13 |
+
os.mkdir(save_path)
|
| 14 |
+
|
| 15 |
+
handlers = [logging.FileHandler(os.path.join(save_path, "log.txt")), logging.StreamHandler()]
|
| 16 |
+
logging.basicConfig(level=logging.INFO,
|
| 17 |
+
format='%(asctime)s %(levelname)s %(message)s',
|
| 18 |
+
handlers=handlers,
|
| 19 |
+
datefmt='%Y-%m-%d %H:%M:%S')
|
| 20 |
+
|
| 21 |
+
return save_path
|
utils/setup_criterion.py
ADDED
|
@@ -0,0 +1,26 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
from torch import nn
|
| 2 |
+
from torchmetrics import StructuralSimilarityIndexMeasure as SSIM
|
| 3 |
+
|
| 4 |
+
class BackboneL2SSIMLoss(nn.Module):
|
| 5 |
+
def __init__(self, ssim_window_size=5, alpha=0.5):
|
| 6 |
+
super(BackboneL2SSIMLoss, self).__init__()
|
| 7 |
+
self.ssim_window_size = ssim_window_size
|
| 8 |
+
self.alpha = alpha
|
| 9 |
+
|
| 10 |
+
self.ssim_loss = SSIM(kernel_size=ssim_window_size).cuda()
|
| 11 |
+
self.l2_loss = nn.MSELoss()
|
| 12 |
+
|
| 13 |
+
def forward(self, backbone, prediction, target):
|
| 14 |
+
ssim_loss_pred = (1.0 - self.ssim_loss(prediction, target))
|
| 15 |
+
l2_loss_pred = self.l2_loss(prediction, target)
|
| 16 |
+
l2_loss_backbone = self.l2_loss(backbone, target)
|
| 17 |
+
|
| 18 |
+
return self.alpha*l2_loss_backbone + l2_loss_pred + ssim_loss_pred
|
| 19 |
+
|
| 20 |
+
def get_criterion(criterion_config):
|
| 21 |
+
criterion_type = criterion_config.type
|
| 22 |
+
if criterion_type == 'backbone-L2-SSIM':
|
| 23 |
+
return BackboneL2SSIMLoss(**criterion_config['params'])
|
| 24 |
+
#TODO: Add more criterion types here (L1, L2 ...)
|
| 25 |
+
else:
|
| 26 |
+
raise ValueError(f"Unsupported criterion type: {criterion_type}")
|
utils/setup_optim_scheduler.py
ADDED
|
@@ -0,0 +1,10 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
import torch
|
| 2 |
+
from torch.optim import lr_scheduler
|
| 3 |
+
|
| 4 |
+
def get_optimizer_scheduler(model, optim_config, scheduler_config):
|
| 5 |
+
optimizer = getattr(torch.optim, optim_config.type)(model.parameters(), **optim_config.params)
|
| 6 |
+
if scheduler_config is not None:
|
| 7 |
+
scheduler = getattr(torch.optim.lr_scheduler, scheduler_config.type)(optimizer, **scheduler_config.params)
|
| 8 |
+
else:
|
| 9 |
+
scheduler = None
|
| 10 |
+
return optimizer, scheduler
|
utils/trainer.py
ADDED
|
@@ -0,0 +1,47 @@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
+
import logging
|
| 2 |
+
|
| 3 |
+
class Trainer():
|
| 4 |
+
def __init__(self, model, optimizer, criterion, scheduler, train_loader, valid_evaluator, test_evaluator, config_train, config_eval):
|
| 5 |
+
self.model = model
|
| 6 |
+
self.optimizer = optimizer
|
| 7 |
+
self.criterion = criterion
|
| 8 |
+
self.scheduler = scheduler
|
| 9 |
+
self.train_loader = train_loader
|
| 10 |
+
self.valid_evaluator = valid_evaluator
|
| 11 |
+
self.test_evaluator = test_evaluator
|
| 12 |
+
self.config_train = config_train
|
| 13 |
+
self.config_eval = config_eval
|
| 14 |
+
|
| 15 |
+
def _train_step(self, input_image, target_image):
|
| 16 |
+
self.optimizer.zero_grad()
|
| 17 |
+
|
| 18 |
+
prediction, x_backbone = self.model(input_image.cuda(), return_backbone=True)
|
| 19 |
+
loss = self.criterion(x_backbone, prediction, target_image.cuda())
|
| 20 |
+
|
| 21 |
+
loss.backward()
|
| 22 |
+
self.optimizer.step()
|
| 23 |
+
if self.scheduler is not None:
|
| 24 |
+
self.scheduler.step()
|
| 25 |
+
|
| 26 |
+
return loss.item()
|
| 27 |
+
|
| 28 |
+
def _train_epoch(self):
|
| 29 |
+
epoch_loss = 0
|
| 30 |
+
self.model.train()
|
| 31 |
+
for data in self.train_loader:
|
| 32 |
+
input_image, target_image, name = data['input_image'], data['target_image'], data['name']
|
| 33 |
+
loss = self._train_step(input_image, target_image)
|
| 34 |
+
epoch_loss += loss
|
| 35 |
+
|
| 36 |
+
return epoch_loss / len(self.train_loader)
|
| 37 |
+
|
| 38 |
+
def train(self):
|
| 39 |
+
for epoch in range(self.config_train.epochs):
|
| 40 |
+
epoch_loss = self._train_epoch()
|
| 41 |
+
logging.info(f"Epoch {epoch+1}/{self.config_train.epochs} | Loss: {epoch_loss}")
|
| 42 |
+
|
| 43 |
+
if self.valid_evaluator is not None and (epoch+1) % self.config_train.valid_every == 0:
|
| 44 |
+
self.valid_evaluator(self.model)
|
| 45 |
+
|
| 46 |
+
self.test_evaluator(self.model, save_results=True if self.valid_evaluator is None else False)
|
| 47 |
+
logging.info("Training finished.")
|