year
stringclasses 13
values | category
stringclasses 9
values | instruction
stringlengths 24
1.55k
| answer
stringlengths 1
4.37k
| input
stringclasses 1
value | output
stringlengths 28
4.77k
| score
int64 3
14
| source
stringclasses 6
values |
|---|---|---|---|---|---|---|---|
2013 | (新课标ⅱ) | 等比数列 $\left\{a_{n}\right\}$ 的前 $n$ 项和为 $S_{n}$, 已知 $S_{3}=a_{2}+10 a_{1}, a_{5}=9$, 则 $a_{1}=(\quad)$
A. $\frac{1}{3}$
B. $-\frac{1}{3}$
C. $\frac{1}{9}$
D. $-\frac{1}{9}$
| C | 解:设等比数列 $\left\{a_{n}\right\}$ 的公比为 $q$,
$\because s_{3}=a_{2}+10 a_{1}, a_{5}=9$
$\therefore\left\{\begin{array}{l}a_{1}+a_{1} q+a_{1} q^{2}=a_{1} q+10 a_{1} \\ a_{1} q^{4}=9\end{array}\right.$, 解得 $\left\{\begin{array}{l}q^{2}=9 \\ a_{1}=\frac{1}{9}\end{array}\right.$.
$\therefore a_{1}=\frac{1}{9}$.
故选: C.
| 5 | 2010-2022_Math_I_MCQs |
|
2013 | (新课标ⅱ) | 已知 $m, n$ 为异面直线, $m \perp$ 平面 $\alpha, n \perp$ 平面 $\beta$. 直线 $\mid$ 满足 $\mid \perp m$, $\mathrm{I} \perp \mathrm{n},|\not \subset \alpha,| \not \subset \beta$, 则 $(\quad)$
A. $\alpha / / \beta$ 且 $\mid / / \alpha$
B. $\alpha \perp \beta$ 且 $l \perp \beta$
C. $\alpha$ 与 $\beta$ 相交, 且交线垂直于।
D. $\alpha$ 与 $\beta$ 相交, 且 交线平行于।
| D | 解: 由 $m \perp$ 平面 $\alpha$, 直线 $\mid$ 满足 $\mid \perp m$, 且 $\mid \subset \alpha$, 所以 $\mid / / \alpha$,
又 $n \perp$ 平面 $\beta, 1 \perp n, \mid \not \subset \beta$, 所以 $I / / \beta$.
由直线 $m, n$ 为异面直线, 且 $m \perp$ 平面 $\alpha, n \perp$ 平面 $\beta$, 则 $\alpha$ 与 $\beta$ 相交, 否则,
若 $\alpha / / \beta$ 则推出 $m / / n$,
与 $m, n$ 异面矛盾.
故 $\alpha$ 与 $\beta$ 相交, 且交线平行于 1 .
故选: D.
| 5 | 2010-2022_Math_I_MCQs |
|
2013 | (新课标ⅱ) | 已知 $(1+\mathrm{ax})(1+\mathrm{x}){ }^{5}$ 的展开式中 $\mathrm{x}^{2}$ 的系数为 5 , 则 $a=(\quad)$
A. -4
B. -3
C. -2
D. -1
| D | 解: 已知 $(1+a x)(1+x)^{5}=(1+a x)\left(1+C_{5}^{1} x+C_{5}^{2} x^{2}+C_{5}^{3} x^{3}+C_{5}^{4} x^{4}+C_{5}^{5} x^{5}\right)$ 展开式中 $x^{2}$ 的系数为 $C_{5}^{2+} a \cdot C_{5}^{1}=5$, 解得 $a=-1$,
故选: D.
| 5 | 2010-2022_Math_I_MCQs |
|
2013 | (新课标ⅱ) | 设 $a=\log _{3} 6, b=\log _{5} 10, c=\log _{7} 14$, 则( )
A. $c>b>a$
B. $b>c>a$
C. $a>c>b$
D. $a>b>c$
| D | 解: 因为 $a=\log _{3} 6=1+\log _{3} 2, b=\log _{5} 10=1+\log _{5} 2, c=\log _{7} 14=1+\log _{7} 2$, 因为 $y=\log _{2} x$ 是增函数, 所以 $\log _{2} 7>\log _{2} 5>\log _{2} 3$,
$\because \log _{2} 7=\frac{1}{\log _{7} 2}, \log _{2} 5=\frac{1}{\log _{5} 2}, \log _{2} 3=\frac{1}{\log _{3} 2}$
所以 $\log _{3} 2>\log _{5} 2>\log _{7} 2$,
所以 $a>b>c$,
故选: D.
| 5 | 2010-2022_Math_I_MCQs |
|
2014 | (新课标ⅰ) | 已知集合 $A=\left\{x \mid x^{2}-2 x-3 \geqslant 0\right\}, B=\{x \mid-2 \leqslant x<2\}$, 则 $A \cap B=(\quad)$
A. $[1,2)$
B. $[-1,1]$
C. $[-1,2)$
D. $[-2,-1]$
| D | 解: 由 $\mathrm{A}$ 中不等式变形得: $(x-3)(x+1) \geqslant 0$,
解得: $x \geqslant 3$ 或 $x \leqslant-1$, 即 $A=(-\infty,-1] \cup[3,+\infty)$,
$\because B=[-2,2)$,
$\therefore A \cap B=[-2,-1]$.
故选:D.
| 5 | 2010-2022_Math_I_MCQs |
|
2014 | (新课标ⅰ) | 2. (5 分 $) \frac{(1+i)^{3}}{(1-i)^{2}}=(\quad)$
A. $1+i$
B. $1-\mathrm{i}$
C. $-1+i$
D. $-1-i$
| D | 解: $\frac{(1+i)^{3}}{(1-i)^{2}}=\frac{2 i(1+i)}{-2 i}=-\quad(1+i)=-1-i$, 故选:D.
| 5 | 2010-2022_Math_I_MCQs |
|
2014 | (新课标ⅰ) | 设函数 $f(x), g(x)$ 的定义域都为 $R$, 且 $f(x)$ 是奇函数, $g(x)$ 是偶函数,则下列结论正确的是( )
A. $f(x) \bullet g(x)$ 是偶函数
B. $|f(x)| \bullet g(x)$ 是奇函数
C. $f(x) \bullet|g(x)|$ 是奇函数
D. $|f(x) \cdot g(x)|$ 是奇函数
| C | 解: $\because \mathrm{f}(\mathrm{x})$ 是奇函数, $\mathrm{g}(\mathrm{x})$ 是偶函数,
$\therefore f(-\mathrm{x})=-\mathrm{f}(\mathrm{x}), g(-\mathrm{x})=\mathrm{g}(\mathrm{x})$,
$f(-x) \cdot g(-x)=-f(x) \cdot g(x)$, 故函数是奇函数, 故 $A$ 错误,
$|f(-x)| \cdot g(-x)=|f(x)| \cdot g(x)$ 为偶函数, 故 B 错误,
$f(-x) \cdot \lg (-x)|=-f(x) \cdot| g(x) \mid$ 是奇函数, 故 C 正确.
$|f(-x) \cdot g(-x)|=|f(x) \cdot g(x)|$ 为偶函数, 故 $D$ 错误,
故选:C.
| 5 | 2010-2022_Math_I_MCQs |
|
2014 | (新课标ⅰ) | 已知 $F$ 为双曲线 $C: x^{2}-m y^{2}=3 m(m>0)$ 的一个焦点, 则点 $F$ 到 $C$ 的一条渐近线的距离为()
A. $\sqrt{3}$
B. 3
C. $\sqrt{3} m$
D. $3 m$
| A | 解:双曲线 $c: x^{2}-m y^{2}=3 m(m>0)$ 可化为 $\frac{x^{2}}{3 m}-\frac{y^{2}}{3}=1$,
$\therefore$ 一个焦点为 $(\sqrt{3 \pi+3}, 0)$, 一条渐近线方程为 $x+\sqrt{m} y=0$,
$\therefore$ 点 $\mathrm{F}$ 到 $\mathrm{C}$ 的一条渐近线的距离为 $\frac{\sqrt{3 \pi+3}}{\sqrt{1+\mathrm{m}}}=\sqrt{3}$.
故选: $A$.
| 5 | 2010-2022_Math_I_MCQs |
|
2014 | (新课标ⅰ) | 4 位同学各自在周六、周日两天中任选一天参加公益活动, 则周六、 周日都有同学参加公益活动的概率为()
A. $\frac{1}{8}$
B. $\frac{3}{8}$
C. $\frac{5}{8}$
D. $\frac{7}{8}$
| D | 解:4 位同学各自在周六、周日两天中任选一天参加公益活动, 共有 $2^{4}=16$ 种情况,
周六、周日都有同学参加公益活动, 共有 $2^{4}-2=16-2=14$ 种情况,
$\therefore$ 所求概率为 $\frac{14}{16}=\frac{7}{8}$.
故选: D.
| 5 | 2010-2022_Math_I_MCQs |
|
2014 | (新课标ⅰ) | 设 $\alpha \in\left(0, \frac{\pi}{2}\right), \beta \in\left(0, \frac{\pi}{2}\right)$, 且 $\tan \alpha=\frac{1+\sin \beta}{\cos \beta}$, 则()
A. $3 \alpha-\beta=\frac{\pi}{2}$
B. $3 \alpha+\beta=\frac{\pi}{2}$
C. $2 \alpha-\beta=\frac{\pi}{2}$
D. $2 \alpha+\beta=\frac{\pi}{2}$
| C | 解:由 $\tan \alpha=\frac{1+\sin \beta}{\cos \beta}$, 得:
$\frac{\sin \alpha}{\cos \alpha}=\frac{1+\sin \beta}{\cos \beta}$
即 $\sin \alpha \cos \beta=\cos \alpha \sin \beta+\cos \alpha$ ,
$\sin (\alpha-\beta)=\cos \alpha=\sin \left(\frac{\pi}{2}-\alpha\right)$,
$\because \alpha \in\left(0, \frac{\pi}{2}\right), \beta \in\left(0, \frac{\pi}{2}\right)$,
$\therefore$ 当 $2 \alpha-\beta=\frac{\pi}{2}$ 时, $\sin (\alpha-\beta)=\sin \left(\frac{\pi}{2}-\alpha\right)=\cos \alpha$ 成立.
故选: C.
| 5 | 2010-2022_Math_I_MCQs |
|
2014 | (新课标ⅰ) | 已知抛物线 $C: y^{2}=8 x$ 的焦点为 $F$, 准线为 $I, P$ 是 $I$ 上一点, $Q$ 是直 线 $P F$ 与 $C$ 的一个交点, 若 $\overrightarrow{F P}=4 \overrightarrow{F Q}$, 则 $|Q F|=(\quad)$
A. $\frac{7}{2}$
B. 3
C. $\frac{5}{2}$
D. 2
| B | 解:设 $Q$ 到 $I$ 的距离为 $d$, 则 $|Q F|=d$,
$\because \overrightarrow{\mathrm{FP}}=4 \overrightarrow{\mathrm{F} 0}$
$\therefore|P Q|=3 d$
$\therefore$ 不妨设直线 $P F$ 的斜率为 $-\frac{2 \sqrt{2} \mathrm{~d}}{\mathrm{~d}}=-2 \sqrt{2}$,
$\because F(2,0)$,
$\therefore$ 直线 $P F$ 的方程为 $y=-2 \sqrt{2}(x-2)$,
与 $y^{2}=8 x$ 联立可得 $x=1$,
$\therefore|Q F|=d=1+2=3$,
故选:B.
| 5 | 2010-2022_Math_I_MCQs |
|
2014 | (新课标ⅰ) | 已知函数 $f(x)=a x^{3}-3 x^{2}+1$, 若 $f(x)$ 存在唯一的零点 $x_{0}$, 且 $x_{0}>$ 0 , 则实数 a 的取值范围是( $)$
A. $(1,+\infty)$
B. $(2,+\infty)$
C. $(-\infty,-1)$
D. $(-\infty,-2)$
| D | 解: $\because f(x)=a x^{3}-3 x^{2}+1$,
$\therefore f^{\prime}(x)=3 a x^{2}-6 x=3 x(a x-2), f(0)=1$;
(1)当 $a=0$ 时, $f(x)=-3 x^{2}+1$ 有两个零点, 不成立; (2)当 $a>0$ 时, $f(x)=a x^{3}-3 x^{2}+1$ 在 $(-\infty, 0)$ 上有零点, 故不成立;
(3)当 $a<0$ 时, $f(x)=a x^{3}-3 x^{2}+1$ 在 $(0,+\infty)$ 上有且只有一个零点;
故 $f(x)=a x^{3}-3 x^{2}+1$ 在 $(-\infty, 0)$ 上没有零点;
而当 $x=\frac{2}{a}$ 时, $f(x)=a x^{3}-3 x^{2}+1$ 在 $(-\infty, 0)$ 上取得最小值;
故 $f\left(\frac{2}{a}\right)=\frac{8}{a^{2}}-3 \cdot \frac{4}{a^{2}}+1>0$;
故 $a<-2$;
综上所述,
实数 $\mathrm{a}$ 的取值范围是 $(-\infty,-2)$;
故选: D.
| 5 | 2010-2022_Math_I_MCQs |
|
2014 | (新课标ⅱ) | 设集合 $M=\{0,1,2\}, N=\left\{x \mid x^{2}-3 x+2 \leqslant 0\right\}$, 则 $M \cap N=(\quad)$
A. $\{1\}$
B. $\{2\}$
C. $\{0,1\}$
D. $\{1,2\}$
| D | 解: $\left.\because N=\left\{x \mid x^{2}-3 x+2 \leqslant 0\right\}=\{x \mid ( x-1) \quad(x-2) \leqslant 0\right\}=\{x \mid 1 \leqslant x \leqslant 2\}$,
$\therefore M \cap N=\{1,2\}$,
故选: D.
| 5 | 2010-2022_Math_I_MCQs |
|
2014 | (新课标ⅱ) | 设复数 $z_{1}, z_{2}$ 在复平面内的对应点关于虚轴对称, $z_{1}=2+i$, 则 $z_{1} z_{2}=$
A. -5
B. 5
C. $-4+i$
D. $-4-i$
| A | 解: $z_{1}=2+i$ 对应的点的坐标为 $(2,1)$,
$\because$ 复数 $z_{1}, z_{2}$ 在复平面内的对应点关于虚轴对称,
$\therefore(2,1)$ 关于虚轴对称的点的坐标为 $(-2,1)$,
则对应的复数, $z_{2}=-2+i$, 则 $z_{1} z_{2}=(2+i)(-2+i)=i^{2}-4=-1-4=-5$,
故选: A.
| 5 | 2010-2022_Math_I_MCQs |
|
2014 | (新课标ⅱ) | 设向量 $\vec{a}, \vec{b}$ 满足 $|\vec{a}+\vec{b}|=\sqrt{10},|\vec{a}-\vec{b}|=\sqrt{6}$, 则 $\vec{a} \bullet \vec{b}=(\quad)$
A. 1
B. 2
C. 3
D. 5
| A | 解: $\because|\vec{a}+\vec{b}|=\sqrt{10},|\vec{a}-\vec{b}|=\sqrt{6}$,
$\therefore$ 分别平方得 $\vec{a}^{2}+2 \vec{a} \bullet \vec{b}+\vec{b}^{2}=10, \vec{a}^{2}-2 \vec{a} \bullet \vec{b}+\vec{b}^{2}=6$,
两式相减得 $4 \vec{a} \bullet \vec{b}=10-6=4$,
即 $\vec{a} \cdot \vec{b}=1$,
故选: A.
| 5 | 2010-2022_Math_I_MCQs |
|
2014 | (新课标ⅱ) | 钝角三角形 $A B C$ 的面积是 $\frac{1}{2}, A B=1, B C=\sqrt{2}$, 则 $A C=(\quad)$
A. 5
B. $\sqrt{5}$
C. 2
D. 1
| B | 解: $\because$ 针角三角形 $A B C$ 的面积是 $\frac{1}{2}, A B=c=1, B C=a=\sqrt{2}$, $\therefore S=\frac{1}{2} \operatorname{acsin} B=\frac{1}{2}$, 即 $\sin B=\frac{\sqrt{2}}{2}$,
当 $B$ 为针角时, $\cos B=-\sqrt{1-\sin ^{2} B}=-\frac{\sqrt{2}}{2}$,
利用余弦定理得: $A C^{2}=A B^{2}+B C^{2}-2 A B \cdot B C \cdot \cos B=1+2+2=5$, 即 $A C=\sqrt{5}$,
当 $B$ 为锐角时, $\cos B=\sqrt{1-\sin ^{2} B}=\frac{\sqrt{2}}{2}$,
利用余弦定理得: $A C^{2}=A B^{2}+B C^{2}-2 A B \cdot B C \cdot \cos B=1+2-2=1$, 即 $A C=1$,
此时 $A B^{2}+A C^{2}=B C^{2}$, 即 $\triangle A B C$ 为直角三角形, 不合题意, 舍去,
则 $A C=\sqrt{5}$.
故选: B.
| 5 | 2010-2022_Math_I_MCQs |
|
2014 | (新课标ⅱ) | 某地区空气质量监测资料表明,一天的空气质量为优良的概率是 0.75 , 连续两天为优良的概率是 0.6 , 已知某天的空气质量为优良, 则随后一天的 空气质量为优良的概率是( $)$
A. 0.8
B. 0.75
C. 0.6
D. 0.45
| A | 解:设随后一天的空气质量为优良的概率为 $p$, 则由题意可得 $0.75 \times$ $p=0.6$,
解得 $p=0.8$,
故选: A.
| 5 | 2010-2022_Math_I_MCQs |
|
2014 | (新课标ⅱ) | 设曲线 $y=a x-\ln (x+1)$ 在点 $(0,0)$ 处的切线方程为 $y=2 x$, 则 $a=($
A. 0
B. 1
C. 2
D. 3
| D | 解: $y^{\prime}=a \frac{1}{x+1}$,
$\therefore y^{\prime}(0)=a-1=2$
$\therefore a=3$.
故选: D.
| 5 | 2010-2022_Math_I_MCQs |
|
2014 | (新课标ⅱ) | 设 $F$ 为抛物线 $C: y^{2}=3 x$ 的焦点,过 $F$ 且倾斜角为 $30^{\circ}$ 的直线交 $C$ 于 $A, B$ 两点, $O$ 为坐标原点, 则 $\triangle O A B$ 的面积为( )
A. $\frac{3 \sqrt{3}}{4}$
B. $\frac{9 \sqrt{3}}{8}$
C. $\frac{63}{32}$
D. $\frac{9}{4}$
| D | 解: 由 $\mathrm{y}^{2}=2 \mathrm{px}$, 得 $2 p=3, \mathrm{p}=\frac{3}{2}$,
则 $F\left(\frac{3}{4}, 0\right)$.
$\therefore$ 过 $A, B$ 的直线方程为 $y=\frac{\sqrt{3}}{3}\left(x-\frac{3}{4}\right)$, 即 $x=\sqrt{3} y+\frac{3}{4}$.
联立 $\left\{\begin{array}{l}y^{2}=3 x \\ x=\sqrt{3} y+\frac{3}{4}\end{array}\right.$, 得 $4 y^{2}-12 \sqrt{3} y-9=0$.
设 $A\left(x_{1}, y_{1}\right) , B\left(x_{2}, y_{2}\right)$ ,
则 $y_{1}+y_{2}=3 \sqrt{3}, y_{1} y_{2}=-\frac{9}{4}$.
$\therefore S_{\triangle O A B}=S_{\triangle O A F}+S_{\triangle O F B}=\frac{1}{2} \times \frac{3}{4}\left|y_{1}-y_{2}\right|=\frac{3}{8} \sqrt{\left(y_{1}+y_{2}\right)^{2}-4 y_{1} y_{2}}=\frac{3}{8} \times \sqrt{(3 \sqrt{3})^{2}+9}=$ $\frac{9}{4}$
故选: D.
| 5 | 2010-2022_Math_I_MCQs |
|
2014 | (新课标ⅱ) | 设函数 $\mathrm{f}(\mathrm{x})=\sqrt{3} \sin \frac{\pi \mathrm{x}}{\mathrm{m}}$, 若存在 $\mathrm{f}(\mathrm{x})$ 的极值点 $\mathrm{x}_{0}$ 满足 $\mathrm{x}_{0}{ }^{2}+\left[\mathrm{f}\left(\mathrm{x}_{0}\right.\right.$ ]$^{2}<m^{2}$ ,则 $m$ 的取值范围是 $(\quad)$
A. $(-\infty,-6) \cup(6,+\infty)$
B. $(-\infty,-4) \cup(4,+\infty)$
C. $(-\infty,-2) \cup(2,+\infty)$
D. $(-\infty,-1) \cup(1,+\infty)$
| C | 解:由题意可得, $f\left(x_{0}\right)= \pm \sqrt{3}$, 即 $\frac{\pi x_{0}}{m}=k \pi+\frac{\pi}{2}, k \in z$, 即 $\mathrm{x}_{0}=\frac{2 k+1}{2} \mathrm{~m}$
再由 $x_{0}{ }^{2}+\left[f\left(x_{0}\right)\right]^{2}<m^{2}$, 即 $x_{0}^{2}+3<m^{2}$, 可得当 $m^{2}$ 最小时, $\left|x_{0}\right|$ 最小, 而 $\left|x_{0}\right|$ 最小为 $\frac{1}{2}|m|$, $\therefore m^{2}>\frac{1}{4} m^{2}+3, \quad \therefore m^{2}>4$.
求得 $m>2$, 或 $m<-2$,
故选: C.
| 5 | 2010-2022_Math_I_MCQs |
|
2015 | (新课标ⅰ) | 设复数 $z$ 满足 $\frac{1+z}{1-z}=i$, 则 $|z|=(\quad)$
A. 1
B. $\sqrt{2}$
C. $\sqrt{3}$
D. 2
| A | 解: $\because$ 复数 $z$ 满足 $\frac{1+z}{1-z}=i$,
$\therefore 1+z=i-z i$,
$\therefore z(1+i)=i-1$,
$\therefore z=\frac{i-1}{i+1}=i$
$\therefore|z|=1$
故选: A.
| 5 | 2010-2022_Math_I_MCQs |
|
2015 | (新课标ⅰ) | 2. (5 分 $) \sin 20^{\circ} \cos 10^{\circ}-\cos 160^{\circ} \sin 10^{\circ}=(\quad )$
A. $\frac{\sqrt{3}}{2}$
B. $\frac{\sqrt{3}}{2}$
C. $-\frac{1}{2}$
D. $\frac{1}{2}$
| D | 解: $\sin 20^{\circ} \cos 10^{\circ}-\cos 160^{\circ} \sin 10^{\circ}$ $=\sin 20^{\circ} \cos 10^{\circ}+\cos 20^{\circ} \sin 10^{\circ}$
$=\sin 30^{\circ}$
$=\frac{1}{2}$
故选: D.
| 5 | 2010-2022_Math_I_MCQs |
|
2015 | (新课标ⅰ) | 设命题 $p: \exists n \in N, n^{2}>2^{n}$, 则 $p$ 为 $(\quad)$
A. $\forall n \in N, n^{2}>2^{n}$
B. $\exists n \in N, n^{2} \leqslant 2^{n}$
C. $\forall n \in N, n^{2} \leqslant 2^{n}$
D. $\exists n \in N, n^{2}=2^{n}$
| C | 解: 命题的否定是: $\forall n \in N, n^{2} \leqslant 2^{n}$,
故选: C.
| 5 | 2010-2022_Math_I_MCQs |
|
2015 | (新课标ⅰ) | 投篮测试中, 每人投 3 次, 至少投中 2 次才能通过测试. 已知某同 学每次投篮投中的概率为 0.6 , 且各次投篮是否投中相互独立, 则该同学通过 测试的概率为 $(\quad)$
A. 0.648
B. 0.432
C. 0.36
D. 0.312
| A | 解:由题意可知: 同学 3 次测试满足 $X \sim B(3,0.6 )$,
该同学通过测试的概率为 $C_{3}^{2}(0.6)^{2} \times(1-0.6)+C_{3}^{3}(0.6)^{3}=0.648$.
故选: $A$.
| 5 | 2010-2022_Math_I_MCQs |
|
2015 | (新课标ⅰ) | 已知 $M\left(x_{0}, y_{0}\right)$ 是双曲线 $C: \frac{x^{2}}{2}-y^{2}=1$ 上的一点, $F_{1}, F_{2}$ 是 $C$ 的左 、右两个焦点, 若 $\overrightarrow{M F_{1}} \cdot \overrightarrow{\mathrm{MF}_{2}}<0$, 则 $\mathrm{y}_{0}$ 的取值范围是( )
A. $\left(\frac{\sqrt{3}}{3}, \frac{\sqrt{3}}{3}\right)$
B. $\left(-\frac{\sqrt{3}}{6}, \frac{\sqrt{3}}{6}\right)$
C. $\left(-\frac{2 \sqrt{2}}{3}, \frac{2 \sqrt{2}}{3}\right)$
D. $\left(-\frac{2 \sqrt{3}}{3}, \frac{2 \sqrt{3}}{3}\right)$
| A | 解:由题意, $\overrightarrow{M_{1}} \cdot \overrightarrow{M_{2}}=\left(-\sqrt{3}-x_{0},-y_{0}\right) \cdot\left(\sqrt{3}-x_{0},-y_{0}\right)$
$$
=\mathrm{x}_{0}^{2}-3+\mathrm{y}_{0}^{2}=3 \mathrm{y}_{0}^{2}-1<0
$$
所以 $-\frac{\sqrt{3}}{3}<y_{0}<\frac{\sqrt{3}}{3}$.
故选: $A$.
| 5 | 2010-2022_Math_I_MCQs |
|
2015 | (新课标ⅰ) | $\left(x^{2}+x+y\right)^{5}$ 的展开式中, $x^{5} y^{2}$ 的系数为 $(\quad)$
A. 10
B. 20
C. 30
D. 60
| C | 解: $\left(x^{2}+x+y\right)^{5}$ 的展开式的通项为 $T_{r+1}=C_{5}^{r}\left(x^{2}+x\right)^{5-r} y^{r}$,
令 $r=2$, 则 $\left(x^{2}+x\right)^{3}$ 的通项为 $C_{3}^{k}\left(x^{2}\right)^{3-k} x^{k}=C_{3}^{k} x^{6-k}$,
令 6- $k=5$, 则 $k=1$,
$\therefore\left(x^{2}+x+y\right)^{5}$ 的展开式中, $x^{5} y^{2}$ 的系数为 $C_{5}^{2} C_{3}^{1}=30$.
故选: C.
| 5 | 2010-2022_Math_I_MCQs |
|
2015 | (新课标ⅱ) | 已知集合 $\mathrm{A}=\{-2,-1,0,1,2\}, B=\{x \mid(x-1)(x+2)<0\}$, 则 $A \cap B=(\quad)$
A. $\{-1,0\}$
B. $\{0,1\}$
C. $\{-1,0,1\}$
D. $\{0,1,2\}$
| A | 解: $\mathrm{B}=\{x \mid-2<x<1\}, \mathrm{A}=\{-2,-1,0,1,2\}$;
$\therefore A \cap B=\{-1,0\}$.
故选: A.
| 5 | 2010-2022_Math_I_MCQs |
|
2015 | (新课标ⅱ) | 若 $a$ 为实数, 且 $(2+a i)(a-2 i)=-4 i$, 则 $a=(\quad)$
A. -1
B. 0
C. 1
D. 2
| B | 解:因为 $(2+a i)(a-2 i)=-4 i$, 所以 $4 a+\left(a^{2}-4\right) i=-4 i$,
$4 a=0$, 并且 $a^{2}-4=-4$,
所以 $a=0$; 故选:B.
| 5 | 2010-2022_Math_I_MCQs |
|
2015 | (新课标ⅱ) | 已知等比数列 $\left\{a_{n}\right\}$ 满足 $a_{1}=3, a_{1}+a_{3}+a_{5}=21$, 则 $a_{3}+a_{5}+a_{7}=(\quad)$
A. 21
B. 42
C. 63
D. 84
| B | 解: $\because a_{1}=3, a_{1}+a_{3}+a_{5}=21$,
$\therefore a_{1}\left(1+q^{2}+q^{4}\right)=21$
$\therefore q^{4}+q^{2}+1=7$
$\therefore q^{4}+q^{2}-6=0$
$\therefore q^{2}=2$
$\therefore a_{3}+a_{5}+a_{7}=a_{1}\left(q^{2}+q^{4}+q^{6}\right)=3 \times(2+4+8)=42$.
故选: B.
| 5 | 2010-2022_Math_I_MCQs |
|
2015 | (新课标ⅱ) | 设函数 $f(x)=\left\{\begin{array}{ll}1+\log _{2}(2-x), & x<1 \\ 2^{x-1}, & x \geqslant 1\end{array}\right.$, 则 $f(-2)+f\left(\log _{2} 12\right)=($ )
A. 3
B. 6
C. 9
D. 12
| C | 解:函数 $f(x)=\left\{\begin{array}{l}1+\log _{2}(2-x), x<1 \\ 2^{x-1}, x \geqslant 1\end{array}\right.$,
即有 $f(-2)=1+\log _{2}(2+2)=1+2=3$,
$f\left(\log _{2} 12\right)=2^{\log _{2} 12-1}=2 \log _{2} 12 \times \frac{1}{2}=12 \times \frac{1}{2}=6$
则有 $f(-2)+f\left(\log _{2} 12\right)=3+6=9$.
故选: C.
| 5 | 2010-2022_Math_I_MCQs |
|
2015 | (新课标ⅱ) | 过三点 $A(1,3), B(4,2), C(1,-7)$ 的圆交 $y$ 轴于 $M, N$ 两点, 则 $|\mathrm{MN}|=(\quad)$
A. $2 \sqrt{6}$
B. 8
C. $4 \sqrt{6}$
D. 10
| C | 解: 设圆的方程为 $x^{2}+y^{2}+D x+E y+F=0$, 则 $\left\{\begin{array}{l}1+9+D+3 E+F=0 \\ 16+4+4 D+2 E+F=0 \\ 1+49+D-7 E+F=0\end{array}\right.$,
$\therefore D=-2, E=4, F=-20$,
$\therefore x^{2}+y^{2}-2 x+4 y-20=0$,
令 $x=0$, 可得 $y^{2}+4 y-20=0$,
$\therefore y=-2 \pm 2 \sqrt{6}$,
$\therefore|\mathrm{MN}|=4 \sqrt{6}$.
故选: C.
| 5 | 2010-2022_Math_I_MCQs |
|
2015 | (新课标ⅱ) | 已知 $A, B$ 为双曲线 $E$ 的左, 右顶点, 点 $M$ 在 $E$ 上, $\triangle A B M$ 为等
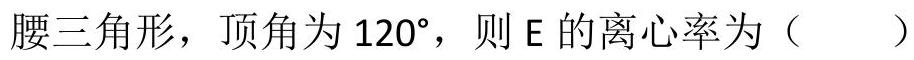
A. $\sqrt{5}$
B. 2
C. $\sqrt{3}$
D. $\sqrt{2}$
| D | 解: 设 $M$ 在双曲线 $\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1$ 的左支上,
且 $M A=A B=2 a, \angle M A B=120^{\circ}$,
则 $M$ 的坐标为 $(-2 a, \sqrt{3} a)$,
代入双曲线方程可得, $\frac{4 a^{2}}{a^{2}}-\frac{3 a^{2}}{b^{2}}=1$
可得 $a=b$,
$c=\sqrt{a^{2}+b^{2}}=\sqrt{2} a$
即有 $\mathrm{e}=\frac{\mathrm{c}}{\mathrm{a}}=\sqrt{2}$.
故选: D.
| 5 | 2010-2022_Math_I_MCQs |
|
2016 | (新课标ⅰ) | 设集合 $A=\left\{x \mid x^{2}-4 x+3<0\right\}, B=\{x \mid 2 x-3>0\}$, 则 $A \cap B=(\quad)$
A. $\left(-3,-\frac{3}{2}\right)$
B. $\left(-3, \frac{3}{2}\right)$
C. $\left(1, \frac{3}{2}\right)$
D. $\left(\frac{3}{2}, 3\right)$
| D | 解: $\because$ 集合 $A=\left\{x \mid x^{2}-4 x+3<0\right\}=(1,3)$,
$\mathrm{B}=\{\mathrm{x} \mid 2 \mathrm{x}-3>0\}=\left(\frac{3}{2},+\infty\right)$,
$\therefore A \cap B=\left(\frac{3}{2}, 3\right)$,
故选:D.
| 5 | 2010-2022_Math_I_MCQs |
|
2016 | (新课标ⅰ) | 设 $(1+i) x=1+y i$, 其中 $x, y$ 是实数, 则 $|x+y i|=(\quad)$
A. 1
B. $\sqrt{2}$
C. $\sqrt{3}$
D. 2
| B | 解: $\because(1+\mathrm{i}) \mathrm{x}=1+\mathrm{yi}$,
$\therefore x+x i=1+y i$,
即 $\left\{\begin{array}{l}x=1 \\ y=x\end{array}\right.$, 解得 $\left\{\begin{array}{l}x=1 \\ y=1\end{array}\right.$, 即 $|x+y i|=|1+i|=\sqrt{2}$, 故选: B.
| 5 | 2010-2022_Math_I_MCQs |
|
2016 | (新课标ⅰ) | 已知等差数列 $\left\{a_{n}\right\}$ 前 9 项的和为 $27, a_{10}=8$, 则 $a_{100}=(\quad)$
A. 100
B. 99
C. 98
D. 97
| C | 解: $\because$ 等差数列 $\left\{a_{n}\right\}$ 前 9 项的和为 $27, \mathrm{~S}_{9}=\frac{9\left(\mathrm{a}_{1}+\mathrm{a}_{9}\right)}{2}=\frac{9 \times 2 \mathrm{a}_{5}}{2}=9 a_{5}$.
$\therefore 9 a_{5}=27, a_{5}=3$,
又 $\because a_{10}=8$,
$\therefore \mathrm{d}=1$,
$\therefore \mathrm{a}_{100}=\mathrm{a}_{5}+95 \mathrm{~d}=98$,
故选: C.
| 5 | 2010-2022_Math_I_MCQs |
|
2016 | (新课标ⅰ) | 某公司的班车在 7: $00,8: 00,8: 30$ 发车, 小明在 7:50 至 8: 30 之间到达发车站乘坐班车, 且到达发车站的时刻是随机的, 则他等车时间不 超过 10 分钟的概率是( $)$
A. $\frac{1}{3}$
B. $\frac{1}{2}$
C. $\frac{2}{3}$
D. $\frac{3}{4}$
| B | 解:设小明到达时间为 $y$, 当 $y$ 在 7: 50 至 8: 00 , 或 8: 20 至 8: 30 时,
小明等车时间不超过 10 分钟,
故 $P=\frac{20}{40}=\frac{1}{2}$,
故选: B.
| 5 | 2010-2022_Math_I_MCQs |
|
2016 | (新课标ⅰ) | 已知方程 $\frac{x^{2}}{m^{2}+n}-\frac{y^{2}}{3 m^{2}-n}=1$ 表示双曲线, 且该双曲线两焦点间的距 离为 4 , 则 $n$ 的取值范围是( $)$
A. $(-1,3)$
B. $(-1, \sqrt{3})$
C. $(0,3)$
D. $(0, \sqrt{3})$
| A | 解: $\because$ 双曲线两焦点间的距离为 $4, \quad \therefore c=2$,
当焦点在 $\mathrm{x}$ 轴上时,
可得: $4=\left(m^{2}+n\right)+\left(3 m^{2}-n\right)$, 解得: $m^{2}=1$,
$\because$ 方程 $\frac{x^{2}}{m^{2}+n}-\frac{y^{2}}{3 m^{2}-n}=1$ 表示双曲线,
$\therefore\left(m^{2}+n\right)\left(3 m^{2}-n\right)>0$, 可得: $(n+1)(3-n)>0$,
解得: $-1<n<3$, 即 $n$ 的取值范围是: $(-1,3)$.
当焦点在 $\mathrm{y}$ 轴上时,
可得: $-4=\left(m^{2}+n\right)+\left(3 m^{2}-n\right)$, 解得: $m^{2}=-1$,
无解.
故选: A.
| 5 | 2010-2022_Math_I_MCQs |
|
2016 | (新课标ⅰ) | 若 $a>b>1,0<c<1$, 则( $)$
A. $a^{c}<b^{c}$
B. $a b^{c}<b a^{c}$
C. $a \log _{b} c<b \log _{a} c$
D. $\log _{a} c<\log _{b} c$
| C | 解: $\because a>b>1,0<c<1$,
$\therefore$ 函数 $f(x)=x^{c}$ 在 $(0,+\infty)$ 上为增函数, 故 $a^{c}>b^{c}$, 故 $\mathrm{A}$ 错误;
函数 $f(x)=x^{c-1}$ 在 $(0,+\infty)$ 上为减函数, 故 $a^{c-1}<b^{c-1}$, 故 $b a^{c}<a b^{c}$, 即 $a b^{c}>$ $b^{c}$; 故 B 错误;
$\log _{a} c<0$, 且 $\log _{b} c<0, \log _{a} b<1$, 即 $\frac{\log _{c} b}{\log _{c} a}=\frac{\log _{a} c}{\log _{b} c}<1$, 即 $\log _{a} c>\log _{b} c$. 故 $D$ 错误;
$0<-\log _{a} c<-\log _{b} c$, 故 $-b \log _{a} c<-a \log _{b} c$, 即 $b \log _{a} c>a \log _{b} c$, 即 $a \log _{b} c<b \log _{a} c$ ,故 C 正确;
故选: C.
| 5 | 2010-2022_Math_I_MCQs |
|
2016 | (新课标ⅱ) | 已知 $z=(m+3)+(m-1) i$ 在复平面内对应的点在第四象限, 则实 数 $m$ 的取值范围是 $(\quad)$
A. $(-3,1)$
B. $(-1,3)$
C. $(1,+\infty)$
D. $(-\infty,-3)$
| A | 解: $z=(m+3)+(m-1) \mathrm{i}$ 在复平面内对应的点在第四象限,
可得: $\left\{\begin{array}{l}m+3>0 \\ m-1<0\end{array}\right.$, 解得 $-3<m<1$.
故选: A.
| 5 | 2010-2022_Math_I_MCQs |
|
2016 | (新课标ⅱ) | 已知集合 $A=\{1,2,3\}, B=\{x \mid ( x+1)(x-2)<0, x \in Z\}$, 则 $A \cup B$ 等于 $(\quad)$
A. $\{1\}$
B. $\{1,2\}$
C. $\{0,1,2,3\}$
D. $\{-1,0,1,2,3\}$
| C | 解: $\because$ 集合 $A=\{1,2,3\}$,
$B=\{x \mid(x+1) \quad(x-2)<0, x \in Z\}=\{0,1\}$,
$\therefore \mathrm{A} \cup \mathrm{B}=\{0,1,2,3\}$.
故选: C.
| 5 | 2010-2022_Math_I_MCQs |
|
2016 | (新课标ⅱ) | 已知向量 $\vec{a}=(1, m), \vec{b}=(3,-2)$, 且 $(\vec{a}+\vec{b}) \perp \vec{b}$, 则 $m=(\quad)$
A. -8
B. -6
C. 6
D. 8
| D | 解: $\because$ 向量 $\vec{a}=(1, m), \vec{b}=(3,-2)$,
$\therefore \vec{a}+\vec{b}=(4, m-2)$,
又 $\because(\vec{a}+\vec{b}) \perp \vec{b}$,
$\therefore 12-2(m-2)=0$
解得: $m=8$,
故选:D.
| 5 | 2010-2022_Math_I_MCQs |
|
2016 | (新课标ⅱ) | 圆 $x^{2}+y^{2}-2 x-8 y+13=0$ 的圆心到直线 $a x+y-1=0$ 的距离为 1 , 则 $a=($
A. $-\frac{4}{3}$
B. $-\frac{3}{4}$
C. $\sqrt{3}$
D. 2
| A | 解:圆 $x^{2}+y^{2}-2 x-8 y+13=0$ 的圆心坐标为: $(1,4)$,
故圆心到直线 $a x+y-1=0$ 的距离 $d=\frac{|a+4-1|}{\sqrt{a^{2}+1}}=1$,
解得: $a=-\frac{4}{3}$,
故选: A.
| 5 | 2010-2022_Math_I_MCQs |
|
2016 | (新课标ⅱ) | 若 $\cos \left(\frac{\pi}{4}-\alpha\right)=\frac{3}{5}$, 则 $\sin 2 \alpha=(\quad)$
A. $\frac{7}{25}$
B. $\frac{1}{5}$
C. $-\frac{1}{5}$
D. $-\frac{7}{25}$
| D | 解: 法 $1^{\circ}: \because \cos \left(\frac{\pi}{4}-\alpha\right)=\frac{3}{5}$,
$\therefore \sin 2 \alpha=\cos \left(\frac{\pi}{2}-2 \alpha\right)=\cos 2\left(\frac{\pi}{4}-\alpha\right)=2 \cos ^{2}\left(\frac{\pi}{4}-\alpha\right)-1=2 \times \frac{9}{25}-1=-\frac{7}{25}$
法 $2^{\circ}: \because \cos \left(\frac{\pi}{4}-\alpha\right)=\frac{\sqrt{2}}{2}(\sin \alpha+\cos \alpha)=\frac{3}{5}$,
$\therefore \frac{1}{2}(1+\sin 2 \alpha)=\frac{9}{25}$,
$\therefore \sin 2 \alpha=2 \times \frac{9}{25}-1=-\frac{7}{25}$,
故选: D.
| 5 | 2010-2022_Math_I_MCQs |
|
2016 | (新课标ⅲ) | 若 $z=1+2 i$, 则 $\frac{4 i}{z \cdot \bar{z}-1}=(\quad)$
A. 1
B. -1
C. i
D. $-\mathrm{i}$
| C | 解: $z=1+2 i$, 则 $\frac{4 i}{z \bar{z}-1}=\frac{4 i}{(1+2 i)(1-2 i)-1}=\frac{4 i}{5-1}=i$.
故选: C.
| 5 | 2010-2022_Math_I_MCQs |
|
2016 | (新课标ⅲ) | 已知向量 $\overrightarrow{\mathrm{BA}}=\left(\frac{1}{2}, \frac{\sqrt{3}}{2}\right), \overrightarrow{\mathrm{BC}}=\left(\frac{\sqrt{3}}{2}, \frac{1}{2}\right)$, 则 $\angle \mathrm{ABC}=(\quad)$
A. $30^{\circ}$
B. $45^{\circ}$
C. $60^{\circ}$
D. $120^{\circ}$
| A | 解: $\overrightarrow{B A} \cdot \overrightarrow{\mathrm{BC}}=\frac{\sqrt{3}}{4}+\frac{\sqrt{3}}{4}=\frac{\sqrt{3}}{2},|\overrightarrow{B A}|=|\overrightarrow{\mathrm{BC}}|=1$;
$\therefore \cos \angle A B C=\frac{\overrightarrow{B A} \cdot \overrightarrow{B C}}{|\overrightarrow{B A}||\overrightarrow{B C}|}=\frac{\sqrt{3}}{2}$
又 $0^{\circ} \leqslant \angle A B C \leqslant 180^{\circ}$;
$\therefore \angle \mathrm{ABC}=30^{\circ}$.
故选: A.
| 5 | 2010-2022_Math_I_MCQs |
|
2016 | (新课标ⅲ) | 若 $\tan a=\frac{3}{4}$, 则 $\cos ^{2} a+2 \sin 2 a=(\quad)$
A. $\frac{64}{25}$
B. $\frac{48}{25}$
C. 1
D. $\frac{16}{25}$
| A | 解: $\because \tan \mathrm{a}=\frac{3}{4}$,
$\therefore \cos ^{2} \alpha+2 \sin 2 \alpha=\frac{\cos ^{2} \alpha+4 \sin \alpha \cos \alpha}{\sin ^{2} \alpha+\cos ^{2} \alpha}=\frac{1+4 \tan \alpha}{\tan ^{2} \alpha+1}=\frac{1+4 \times \frac{3}{4}}{\frac{9}{16}+1}=\frac{64}{25}$.
故选: A.
| 5 | 2010-2022_Math_I_MCQs |
|
2016 | (新课标ⅲ) | 已知 $a=2^{\frac{4}{3}}, b=3^{\frac{2}{3}}, c=25^{\frac{1}{3}}$, 则 ( )
A. $b<a<c$
B. $a<b<c$
C. $\mathrm{b}<\mathrm{c}<\mathrm{a}$
D. $c<a<b$
| A | 解: $\because a=2^{\frac{4}{3}}=4^{\frac{2}{3}}$,
$b=3^{\frac{2}{3}}$
$\mathrm{C}=25^{\frac{1}{3}}=5^{\frac{2}{3}}$
综上可得: $b<a<c$,
故选: A.
| 5 | 2010-2022_Math_I_MCQs |
|
2016 | (新课标ⅲ) | 在封闭的直三棱柱 $A B C-A_{1} B_{1} C_{1}$ 内有一个体积为 $V$ 的球, 若 $A B \perp$ $B C, A B=6, B C=8, A A_{1}=3$, 则 $V$ 的最大值是 $(\quad)$
A. $4 \pi$
B. $\frac{9 \pi}{2}$
C. $6 \pi$
D. $\frac{32 \pi}{3}$
| B | 解: $\because \mathrm{AB} \perp \mathrm{BC}, \mathrm{AB}=6, \mathrm{BC}=8$,
$\therefore A C=10$ 故三角形 $A B C$ 的内切圆半径 $r=\frac{6+8-10}{2}=2$,
又由 $\mathrm{AA}_{1}=3$,
故直三棱柱 $A B C-A_{1} B_{1} C_{1}$ 的内切球半径为 $\frac{3}{2}$,
此时 $\vee$ 的最大值 $\frac{4}{3} \pi \cdot\left(\frac{3}{2}\right)^{3}=\frac{9 \pi}{2}$,
故选: B.
| 5 | 2010-2022_Math_I_MCQs |
|
2016 | (新课标ⅲ) | 已知 $O$ 为坐标原点, $F$ 是椭圆 $C: \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1(a>b>0)$ 的左焦点, $A, B$ 分别为 $C$ 的左, 右顶点. $P$ 为 $C$ 上一点, 且 $P F \perp x$ 轴, 过点 $A$ 的直线 I 与线段 $P F$ 交于点 $M$, 与 $y$ 轴交于点 $E$. 若直线 $B M$ 经过 $O E$ 的中点, 则 $C$ 的离心率为 $(\quad)$
A. $\frac{1}{3}$
B. $\frac{1}{2}$
C. $\frac{2}{3}$
D. $\frac{3}{4}$
| A | 解:由题意可设 $F(-c, 0), A(-a, 0), B(a, 0)$,
设直线 $A E$ 的方程为 $y=k(x+a)$,
令 $x=-c$, 可得 $M(-c, k(a-c))$, 令 $x=0$, 可得 $E(0, k a)$,
设 $O E$ 的中点为 $H$, 可得 $H\left(0, \frac{k a}{2}\right)$, 由 $B, H, M$ 三点共线,可得 $k_{B H}=k_{B M}$,
即为 $\frac{\frac{k a}{2}}{-a}=\frac{k(a-c)}{-c-a}$
化简可得 $\frac{a-c}{a+c}=\frac{1}{2}$, 即为 $a=3 c$,
可得 $\mathrm{e}=\frac{c}{\mathrm{a}}=\frac{1}{3}$.
另解: 由 $\triangle A M F \backsim \triangle A E O$,
可得 $\frac{a-c}{a}=\frac{M F}{O E}$,
由 $\triangle B O H \backsim \triangle B F M$,
可得 $\frac{a}{a+c}=\frac{O H}{F M}=\frac{O E}{2 F M M}$,
即有 $\frac{2(a-c)}{a}=\frac{a+c}{a}$ 即 $a=3 c$,
可得 $\mathrm{e}=\frac{c}{\mathrm{a}}=\frac{1}{3}$.
故选: A.
| 5 | 2010-2022_Math_I_MCQs |
|
2016 | (新课标ⅲ) | 定义“规范 01 数列” $\left\{a_{n}\right\}$ 如下: $\left\{a_{n}\right\}$ 共有 $2 m$ 项, 其中 $m$ 项为 $0, m$ 项 为 1 , 且对任意 $k \leqslant 2 m, a_{1}, a_{2}, \ldots, a_{k}$ 中 0 的个数不少于 1 的个数, 若 $m=4$, 则不同的“规范 01 数列”共有()
A. 18 个
B. 16 个
C. 14 个
D. 12 个
\section{
| C | 解:由题意可知, “规范 01 数列”有偶数项 $2 \mathrm{~m}$ 项, 且所含 0 与 1 的个 数相等, 首项为 0 , 末项为 1 , 若 $m=4$, 说明数列有 8 项, 满足条件的数列 有:
$0,0,0,0,1,1,1,1 ; 0,0,0,1,0,1,1,1 ; 0,0,0,1,1$, $0,1,1 ; 0,0,0,1,1,1,0,1 ; 0,0,1,0,0,1,1,1$;
$0,0,1,0,1,0,1,1 ; 0,0,1,0,1,1,0,1 ; 0,0,1,1,0$, $1,0,1 ; 0,0,1,1,0,0,1,1 ; 0,1,0,0,0,1,1,1$;
$0,1,0,0,1,0,1,1 ; 0,1,0,0,1,1,0,1 ; 0,1,0,1,0$, $0,1,1 ; 0,1,0,1,0,1,0,1$. 共 14 个.
故选: C.
| 5 | 2010-2022_Math_I_MCQs |
|
2017 | (新课标ⅰ) | 已知集合 $A=\{x \mid x<1\}, B=\left\{x \mid 3^{x}<1\right\}$, 则()
A. $A \cap B=\{x \mid x<0\}$ B. $A \cup B=R$
C. $\mathrm{A} \cup \mathrm{B}=\{\mathrm{x} \mid \mathrm{x}>1\}$
D. $A \cap B=\varnothing$
| A | 解: $\because$ 集合 $A=\{x \mid x<1\}$,
$B=\left\{x \mid 3^{x}<1\right\}=\{x \mid x<0\}$
$\therefore A \cap B=\{x \mid x<0\}$, 故 $A$ 正确, $D$ 错误;
$A \cup B=\{x \mid x<1\}$, 故 $B$ 和 $C$ 都错误.
故选: A.
| 5 | 2010-2022_Math_I_MCQs |
|
2017 | (新课标ⅰ) | 设有下面四个命题
$p_{1}$ : 若复数 $z$ 满足 $\frac{1}{z} \in R$, 则 $z \in R$;
$p_{2}$ : 若复数 $z$ 满足 $z^{2} \in R$, 则 $z \in R$;
$p_{3}$ :若复数 $z_{1}, z_{2}$ 满足 $z_{1} z_{2} \in R$, 则 $z_{1}=\overline{z_{2}}$;
$p_{4}$ : 若复数 $z \in R$, 则 $z \in R$.
其中的真命题为( $)$
A. $\mathrm{p}_{1}, \mathrm{p}_{3}$
B. $\mathrm{p}_{1}, \mathrm{p}_{4}$
C. $p_{2}, p_{3}$
D. $p_{2}, p_{4}$
| B | 解:若复数 $z$ 满足 $\frac{1}{z} \in R$, 则 $z \in R$, 故命题 $p_{1}$ 为真命题; $p_{2}$ : 复数 $z=i$ 满足 $z^{2}=-1 \in R$, 则 $z \notin R$, 故命题 $p_{2}$ 为假命题;
$p_{3}$ :若复数 $z_{1}=i, z_{2}=2 i$ 满足 $z_{1} z_{2} \in R$, 但 $z_{1} \neq \overline{z_{2}}$, 故命题 $p_{3}$ 为假命题;
$p_{4}$ : 若复数 $z \in R$, 则 $z=z \in R$, 故命题 $p_{4}$ 为真命题.
故选: B.
| 5 | 2010-2022_Math_I_MCQs |
|
2017 | (新课标ⅰ) | 记 $S_{n}$ 为等差数列 $\left\{a_{n}\right\}$ 的前 $n$ 项和. 若 $a_{4}+a_{5}=24, S_{6}=48$, 则 $\left\{a_{n}\right\}$ 的公 差为 $(\quad)$
A. 1
B. 2
C. 4
D. 8
| C | 解: $\because S_{n}$ 为等差数列 $\left\{a_{n}\right\}$ 的前 $n$ 项和, $a_{4}+a_{5}=24, S_{6}=48$, $\therefore\left\{\begin{array}{l}a_{1}+3 d+a_{1}+4 d=24 \\ 6 a_{1}+\frac{6 \times 5}{2} d=48\end{array}\right.$,
解得 $\mathrm{a}_{1}=-2, \mathrm{~d}=4$,
$\therefore\left\{a_{n}\right\}$ 的公差为 4 .
故选: C.
| 5 | 2010-2022_Math_I_MCQs |
|
2017 | (新课标ⅰ) | 函数 $f(x)$ 在 $(-\infty,+\infty)$ 单调递减, 且为奇函数. 若 $f(1)=-1$ , 则满足 $-1 \leqslant f(x-2) \leqslant 1$ 的 $x$ 的取值范围是 $(\quad)$
A. $[-2,2]$
B. $[-1,1]$
C. $[0,4]$
D. $[1,3]$
| D | 解: $\because$ 函数 $f(x)$ 为奇函数.
若 $f(1)=-1$, 则 $f(-1)=1$,
又 $\because$ 函数 $f(x)$ 在 $(-\infty,+\infty)$ 单调递减, $-1 \leqslant f(x-2) \leqslant 1$,
$\therefore f(1) \leqslant f(x-2) \leqslant f(-1)$
$\therefore-1 \leqslant x-2 \leqslant 1$
解得: $x \in[1,3]$,
故选: D.
| 5 | 2010-2022_Math_I_MCQs |
|
2017 | (新课标ⅰ) | $\left(1+\frac{1}{x^{2}}\right)(1+x){ }^{6}$ 展开式中 $x^{2}$ 的系数为( $)$
A. 15
B. 20
C. 30
D. 35
| C | 解: $\left(1+\frac{1}{x^{2}}\right)(1+x)^{6}$ 展开式中:
若 $\left(1+\frac{1}{x^{2}}\right)=\left(1+x^{-2}\right)$ 提供常数项 1, 则 $(1+x)^{6}$ 提供含有 $x^{2}$ 的项, 可得展开 式中 $x^{2}$ 的系数:
若 $\left(1+\frac{1}{x^{2}}\right)$ 提供 $x^{-2}$ 项, 则 $(1+x)^{6}$ 提供含有 $x^{4}$ 的项, 可得展开式中 $x^{2}$ 的系数:
由 $(1+x) 6$ 通项公式可得 $\mathrm{C}_{6}^{r} \mathrm{x}^{\mathrm{r}}$. 可知 $r=2$ 时, 可得展开式中 $x^{2}$ 的系数为 $C_{6}^{2}=15$.
可知 $r=4$ 时, 可得展开式中 $x^{2}$ 的系数为 $C_{6}^{4}=15$.
$\left(1+\frac{1}{x^{2}}\right)(1+x)^{6}$ 展开式中 $x^{2}$ 的系数为: $15+15=30$.
故选: C.
| 5 | 2010-2022_Math_I_MCQs |
|
2017 | (新课标ⅰ) | 已知曲线 $C_{1}: y=\cos x, C_{2}: y=\sin \left(2 x+\frac{2 \pi}{3}\right)$, 则下面结论正确的是( )
A. 把 $C_{1}$ 上各点的横坐标伸长到原来的 2 倍, 纵坐标不变, 再把得到的曲线 向右平移 $\frac{\pi}{6}$ 个单位长度, 得到曲线 $\mathrm{c}_{2}$
B. 把 $C_{1}$ 上各点的横坐标伸长到原来的 2 倍, 纵坐标不变, 再把得到的曲线 向左平移 $\frac{\pi}{12}$ 个单位长度, 得到曲线 $\mathrm{C}_{2}$
C. 把 $\mathrm{C}_{1}$ 上各点的横坐标缩短到原来的 $\frac{1}{2}$ 倍, 纵坐标不变, 再把得到的曲线向 右平移 $\frac{\pi}{6}$ 个单位长度, 得到曲线 $C_{2}$
D. 把 $C_{1}$ 上各点的横坐标缩短到原来的 $\frac{1}{2}$ 倍, 纵坐标不变, 再把得到的曲线向 左平移 $\frac{\pi}{12}$ 个单位长度, 得到曲线 $C_{2}$
| D | 解: 把 $\mathrm{C}_{1}$ 上各点的横坐标缩短到原来的 $\frac{1}{2}$ 倍, 纵坐标不变, 得到函数 $y=\cos 2 x$ 图象, 再把得到的曲线向左平移 $\frac{\pi}{12}$ 个单位长度, 得到函数 $y=\cos 2\left(x^{+}\right.$ $\left.\frac{\pi}{12}\right)=\cos \left(2 x+\frac{\pi}{6}\right)=\sin \left(2 x+\frac{2 \pi}{3}\right)$ 的图象, 即曲线 $C_{2}$,
故选: D.
| 5 | 2010-2022_Math_I_MCQs |
|
2017 | (新课标ⅰ) | 设 $x 、 y 、 z$ 为正数, 且 $2^{x}=3^{y}=5^{2}$, 则 ( )
A. $2 x<3 y<5 z$
B. $5 z<2 x<3 y$
C. $3 y<5 z<2 x$
D. $3 y<2 x<5 z$
| D | 解: $x 、 y 、 z$ 为正数,
令 $2^{x}=3^{y}=5^{z}=k>1 . \quad \lg k>0$.
则 $x=\frac{\operatorname{lgk}}{\lg 2}, y=\frac{\operatorname{lgk}}{\lg 3}, z=\frac{\operatorname{lgk}}{\lg 5}$.
$\therefore 3 y=\frac{\operatorname{lgk}}{\lg \sqrt[3]{3}}, 2 x=\frac{\operatorname{lgk}}{\lg \sqrt{2}}, 5 \mathrm{z}=\frac{\operatorname{lgk}}{\lg \sqrt[5]{5}}$.
$\because \sqrt[3]{3}=\sqrt[6]{9}>\sqrt[6]{8}=\sqrt{2}, \sqrt{2}=\sqrt[10]{32}>\sqrt[10]{25}=\sqrt[5]{5}$
$\therefore \lg \sqrt[3]{3}>\lg \sqrt{2}>\lg \sqrt[5]{5}>0$
$\therefore 3 y<2 x<5 z$.
另解: $x 、 y 、 z$ 为正数,
令 $2^{x}=3^{y}=5^{2}=k>1 . \quad \lg k>0$.
则 $x=\frac{\operatorname{lgk}}{\lg 2}, y=\frac{\operatorname{lgk}}{\lg 3}, z=\frac{\operatorname{lgk}}{\lg 5}$.
$\therefore \frac{2 x}{3 y}=\frac{2}{3} \times \frac{\lg 3}{\lg 2}=\frac{\lg 9}{\lg 8}>1$, 可得 $2 x>3 y$,
$\frac{5 z}{2 x}=\frac{5}{2} \times \frac{\lg 2}{\lg 5}=\frac{\lg 2^{5}}{\lg 5^{2}}>1$. 可得 $5 z>2 x$.
综上可得: $5 z>2 x>3 y$.
解法三: 对 $\mathrm{k}$ 取特殊值, 也可以比较出大小关系.
故选:D.
| 5 | 2010-2022_Math_I_MCQs |
|
2017 | (新课标ⅰ) | 几位大学生响应国家的创业号召, 开发了一款应用软件. 为激发大 家学习数学的兴趣, 他们推出了“解数学题获取软件激活码”的活动. 这款软 件的激活码为下面数学问题的答案: 已知数列 $1,1,2,1,2,4,1,2,4$, $8,1,2,4,8,16, \ldots$, 其中第一项是 $2^{0}$, 接下来的两项是 $2^{0}, 2^{1}$, 再接下 来的三项是 $2^{0}, 2^{1}, 2^{2}$, 依此类推. 求满足如下条件的最小整数 $N: N>100$ 且该数列的前 $\mathrm{N}$ 项和为 2 的整数幂. 那么该款软件的激活码是()
A. 440
B. 330
C. 220
D. 110
| A | 解: 设该数列为 $\left\{a_{n}\right\}$, 设 $b_{n}=\frac{a_{(n-1) n}}{2}+1+\ldots+\frac{a_{n(n+1)}}{2}=2^{n+1}-1, \quad\left(n \in N_{+}\right)$, 则 $\sum_{i=1}^{n} b_{i}=\sum_{i=1}^{\frac{n(n+1)}{2}} a_{i}$,
由题意可设数列 $\left\{a_{n}\right\}$ 的前 $N$ 项和为 $S_{N}$, 数列 $\left\{b_{n}\right\}$ 的前 $n$ 项和为 $T_{n}$, 则
$$
T_{n}=2^{1}-1+2^{2}-1+\ldots+2^{n+1}-1=2^{n+1}-n-2
$$
可知当 $N$ 为 $\frac{n(n+1)}{2}$ 时 $\left(n \in N_{+}\right)$, 数列 $\left\{a_{n}\right\}$ 的前 $N$ 项和为数列 $\left\{b_{n}\right\}$ 的前 $n$ 项和, 即为 $2^{n+1}-n-2$,
容易得到 $N>100$ 时, $n \geqslant 14$,
A 项, 由 $\frac{29 \times 30}{2}=435,440=435+5$, 可知 $S_{440}=T_{29}+b_{5}=2^{30}-29-2+2^{5}-1=2^{30}$, 故 A 项符合题意.
$B$ 项, 仿上可知 $\frac{25 \times 26}{2}=325$, 可知 $S_{330}=T_{25}+b_{5}=2^{26}-25-2+2^{5}-1=2^{26+4}$, 显然不 为 2 的整数幂, 故 $B$ 项不符合题意.
$C$ 项, 仿上可知 $\frac{20 \times 21}{2}=210$, 可知 $S_{220}=T_{20}+b_{10}=2^{21}-20-2+2^{10}-1=2^{21}+2^{10}-23$, 显然不为 2 的整数幂, 故 C 项不符合题意. $\mathrm{D}$ 项, 仿上可知 $\frac{14 \times 15}{2}=105$, 可知 $\mathrm{S}_{110}=T_{14}+b_{5}=2^{15}-14-2^{+} 2^{5}-1=2^{15}+15$, 显然 不为 2 的整数幂, 故 $D$ 项不符合题意.
故选 A.
方法 二 : 由 题 意可 知 : 第一项, $\frac{2^{0}, 2^{1}}{\text { 第二项 }}, \frac{2^{0}, 2^{1}, 2^{2}}{\text { 第三项 }}, \ldots$
$$
\frac{2^{0}, 2^{1}, 2^{2}, \cdots, 2^{\mathrm{n}-1}}{\text { 第n项 }},
$$
根据等比数列前 $n$ 项和公式, 求得每项和分别为: $2^{1-} 1,2^{2-} 1,2^{3-} 1, \ldots, 2^{n_{-}} 1$
每项含有的项数为: $1,2,3, \ldots, n$,
总共的项数为 $\mathrm{N}=1+2+3+\ldots+n=\frac{(1+n) n}{2}$,
所有项数的和为 $S_{n}: 2^{1-} 1+2^{2}-1+2^{3}-1+\ldots+2^{n}-1=\left(2^{1}+2^{2}+2^{3}+\ldots+2^{n}\right)-n=$
$$
\frac{2\left(1-2^{n}\right)}{1-2}-n=2^{n+1}-2-n
$$
由题意可知: $2^{n+1}$ 为 2 的整数幂. 只需将 $-2-n$ 消去即可,
则(1) $1+2+(-2-n)=0$, 解得: $n=1$, 总共有 $\frac{(1+1) \times 1}{2}+2=3$, 不满足 $N>100$,
(2) $1+2+4+(-2-n)=0$, 解得: $n=5$, 总共有 $\frac{(1+5) \times 5}{2}+3=18$, 不满足 $N>100$,
(3) $1+2+4+8+(-2-n)=0$, 解得: $n=13$, 总共有 $\frac{(1+13) \times 13}{2}+4=95$, 不满足 $N>$ 100 ,
(4) $1+2+4+8+16+(-2-n)=0$, 解得: $n=29$, 总共有 $\frac{(1+29) \times 29}{2}+5=440$, 满足 $N$ $>100$
$\therefore$ 该款软件的激活码 440 .
| 5 | 2010-2022_Math_I_MCQs |
|
2017 | (新课标ⅱ) | 1. $(5$ 分 $) \frac{3+i}{1+i}=(\quad)$
A. $1+2 i$
B. $1-2 i$
C. $2+i$
D. $2-\mathrm{i}$
| D | 解 $: \frac{3+i}{1+i}=\frac{(3+i)(1-i)}{(1+i)(1-i)}=\frac{4-2 i}{2}=2-i$,
故选:D.
| 5 | 2010-2022_Math_I_MCQs |
|
2017 | (新课标ⅱ) | 设集合 $A=\{1,2,4\}, B=\left\{x \mid x^{2}-4 x+m=0\right\}$. 若 $A \cap B=\{1\}$, 则 $B=(\quad)$
A. $\{1,-3\}$
B. $\{1,0\}$
C. $\{1,3\}$
D. $\{1,5\}$
| C | 解:集合 $\mathrm{A}=\{1,2,4\}, B=\left\{x \mid x^{2}-4 x+m=0\right\}$.
若 $A \cap B=\{1\}$, 则 $1 \in A$ 且 $1 \in B$, 可得 $1-4+m=0$, 解得 $m=3$,
即有 $B=\left\{x \mid x^{2}-4 x+3=0\right\}=\{1,3\}$.
故选: C.
| 5 | 2010-2022_Math_I_MCQs |
|
2017 | (新课标ⅱ) | 我国古代数学名著《算法统宗》中有如下问题: “远看巍巍塔七层, 红光点点倍加增, 共灯三百八十一, 请问尖头几盏灯? "意思是: 一座 7 层塔 共挂了 381 或灯, 且相邻两层中的下一层灯数是上一层灯数的 2 倍, 则塔的 顶层共有灯()
A. 1 盏
B. 3 盏
C. 5 或
D. 9 或
| B | 解:设塔顶的 $a_{1}$ 盏灯,
由题意 $\left\{a_{n}\right\}$ 是公比为 2 的等比数列,
$\therefore S_{7}=\frac{a_{1}\left(1-2^{7}\right)}{1-2}=381$,
解得 $\mathrm{a}_{1}=3$.
故选:B.
| 5 | 2010-2022_Math_I_MCQs |
|
2017 | (新课标ⅱ) | 安排 3 名志愿者完成 4 项工作, 每人至少完成 1 项, 每项工作由 1 人完成, 则不同的安排方式共有( $)$
A. 12 种
B. 18 种
C. 24 种
D. 36 种
| D | 解: 4 项工作分成 3 组, 可得: $C_{4}^{2}=6$, 安排 3 名志愿者完成 4 项工作, 每人至少完成 1 项, 每项工作由 1 人完成, 可得: $6 \times \mathrm{A}_{3}^{3}=36$ 种.
故选: D.
| 5 | 2010-2022_Math_I_MCQs |
|
2017 | (新课标ⅱ) | 甲、乙、丙、丁四位同学一起去问老师询问成语竞赛的成绩. 老师 说: 你们四人中有 2 位优秀, 2 位良好, 我现在给甲看乙、丙的成绩, 给乙 看丙的成绩, 给丁看甲的成绩. 看后甲对大家说: 我还是不知道我的成绩. 根据以上信息,则( $)$
A. 乙可以知道四人的成绩
B. 丁可以知道四人的成绩
C. 乙、丁可以知道对方的成绩
D. 乙、丁可以知道自己的成绩
| D | 解:四人所知只有自己看到, 老师所说及最后甲说话,
甲不知自己的成绩
$\rightarrow$ 乙丙必有一优一良, (若为两优, 甲会知道自己的成绩; 若是两良, 甲也会 知道自己的成绩)
$\rightarrow$ 乙看到了丙的成绩, 知自己的成绩
$\rightarrow$ 丁看到甲、丁也为一优一良,丁知自己的成绩,
给甲看乙丙成绩, 甲不知道自已的成绩, 说明乙丙一优一良, 假定乙丙都是优, 则甲是良, 假定乙丙都是良, 则甲是优, 那么甲就知道自已的成绩了. 给乙 看丙成绩, 乙没有说不知道自己的成绩, 假定丙是优, 则乙是良, 乙就知道 自己成绩. 给丁看甲成绩, 因为甲不知道自己成绩, 乙丙是一优一良, 则甲 丁也是一优一良, 丁看到甲成绩, 假定甲是优, 则丁是良, 丁肯定知道自已 的成绩了 故选: D.
| 5 | 2010-2022_Math_I_MCQs |
|
2017 | (新课标ⅱ) | 若双曲线 $c: \frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1(a>0, b>0)$ 的一条渐近线被圆 $(x-2)$ ${ }^{2}+y^{2}=4$ 所截得的弦长为 2 , 则 $C$ 的离心率为 ( )
A. 2
B. $\sqrt{3}$
C. $\sqrt{2}$
D. $\frac{2 \sqrt{3}}{3}$
| A | 解 双曲线 $c: \frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1(a>0, b>0)$ 的一条渐近线不妨为 $b x+a y=0$
圆 $(x-2)^{2}+y^{2}=4$ 的圆心 $(2,0)$, 半径为: 2 ,
双曲线 $C: \frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1(a>0, b>0)$ 的一条渐近线被圆 $(x-2)^{2}+y^{2}=4$ 所截得 的弦长为 2 , 可得圆心到直线的距离为: $\sqrt{2^{2}-1^{2}}=\sqrt{3}=\frac{|2 b|}{\sqrt{a^{2}+b^{2}}}$,
解得: $\frac{4 c^{2}-4 \mathrm{a}^{2}}{\mathrm{c}^{2}}=3$, 可得 $\mathrm{e}^{2}=4$, 即 $\mathrm{e}=2$.
故选: A.
| 5 | 2010-2022_Math_I_MCQs |
|
2017 | (新课标ⅱ) | 若 $x=-2$ 是函数 $f(x)=\left(x^{2}+a x-1\right) e^{x-1}$ 的极值点, 则 $f(x)$ 的极 小值为 $(\quad)$
A. -1
B. $-2 e^{-3}$
C. $5 \mathrm{e}^{-3}$
D. 1
| A | 解:函数 $f(x)=\left(x^{2}+a x-1\right) e^{x-1}$,
可得 $f^{\prime}(x)=(2 x+a) e^{x-1+}\left(x^{2}+a x-1\right) e^{x-1}$,
$x=-2$ 是函数 $f(x)=\left(x^{2}+a x-1\right) e^{x-1}$ 的极值点,
可得: $f^{\prime}(-2)=(-4+a) e^{-3}+(4-2 a-1) e^{-3}=0$, 即 $-4+a+(3-2 a)=0$.
解得 $a=-1$.
可得 $f^{\prime}(x)=(2 x-1) e^{x-1+}\left(x^{2}-x-1\right) e^{x-1}$,
$=\left(x^{2}+x-2\right) e^{x-1}$, 函数的极值点为: $x=-2, x=1$,
当 $x<-2$ 或 $x>1$ 时, $f^{\prime}(x)>0$ 函数是增函数, $x \in(-2,1 )$ 时, 函数是减函 数,
$x=1$ 时, 函数取得极小值: $f(1)=\left(1^{2}-1-1\right) e^{1-1}=-1$.
故选: A.
| 5 | 2010-2022_Math_I_MCQs |
|
2017 | (新课标ⅲ) | 已知集合 $A=\left\{(x, y) \mid x^{2}+y^{2}=1\right\}, B=\{(x, y) \mid y=x\}$, 则 $A \cap B$ 中元 素的个数为 $(\quad)$
A. 3
B. 2
C. 1
D. 0
| B | 解: 由 $\left\{\begin{array}{l}x^{2}+y^{2}=1 \\ y=x\end{array}\right.$, 解得: $\left\{\begin{array}{l}x=\frac{\sqrt{2}}{2} \\ y=\frac{\sqrt{2}}{2}\end{array}\right.$ 或 $\left\{\begin{array}{c}x=-\frac{\sqrt{2}}{2} \\ y=\frac{\sqrt{2}}{2}\end{array}\right.$,
$\therefore A \cap B$ 的元素的个数是 2 个,
故选: B.
| 5 | 2010-2022_Math_I_MCQs |
|
2017 | (新课标ⅲ) | 设复数 $z$ 满足 $(1+i) \quad z=2 i$, 则 $|z|=(\quad)$
A. $\frac{1}{2}$
B. $\frac{\sqrt{2}}{2}$
C. $\sqrt{2}$
D. 2
| C | 解: $\because(1+\mathrm{i}) \mathrm{z}=2 \mathrm{i}, \quad \therefore(1-\mathrm{i})(1+\mathrm{i}) \quad \mathrm{z}=2 \mathrm{i}(1-\mathrm{i}), \mathrm{z}=\mathrm{i}+1$.
则 $|z|=\sqrt{2}$.
故选: C.
| 5 | 2010-2022_Math_I_MCQs |
|
2017 | (新课标ⅲ) | $(\mathrm{x}+\mathrm{y})(2 \mathrm{x}-\mathrm{y})^{5}$ 的展开式中的 $x^{3} \mathrm{y}^{3}$ 系数为 $(\quad)$
A. -80
B. -40
C. 40
D. 80
| C | 解: $(2 x-y)^{5}$ 的展开式的通项公式: $T_{r+1}=\left[_{5}^{r}(2 x)^{5-r}(-y)^{r}=2^{5-r}\right.$ $(-1){ }^{r}\left[{ }_{5}^{r} x^{5-r} y\right.$
令 $5-r=2, r=3$, 解得 $r=3$.
令 $5-r=3, r=2$, 解得 $r=2$.
$\therefore(x+y)(2 x-y)^{5}$ 的展开式中的 $x^{3} y^{3}$ 系数 $=2^{2} \times(-1)^{3}\left[_{5}^{3}+2^{3} \times 1 \times\left[_{5}^{2}=40\right.\right.$. 故选: C.
| 5 | 2010-2022_Math_I_MCQs |
|
2017 | (新课标ⅲ) | 已知双曲线 $C: \frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1 \quad(a>0, b>0)$ 的一条渐近线方程为 $y=\frac{\sqrt{5}}{2} x$, 且与椭圆 $\frac{x^{2}}{12}+\frac{y^{2}}{3}=1$ 有公共焦点, 则 $C$ 的方程为 $(\quad)$
A. $\frac{x^{2}}{8}-\frac{y^{2}}{10}=1$
B. $\frac{x^{2}}{4}-\frac{y^{2}}{5}=1$
C. $\frac{x^{2}}{5}-\frac{y^{2}}{4}=1$
D. $\frac{x^{2}}{4}-\frac{y^{2}}{3}=1$
| B | 解: 椭圆 $\frac{x^{2}}{12}+\frac{y^{2}}{3}=1$ 的焦点坐标 $( \pm 3,0)$,
则双曲线的焦点坐标为 $( \pm 3,0)$, 可得 $c=3$,
双曲线 C: $\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1 \quad(a>0, b>0)$ 的一条渐近线方程为 $y=\frac{\sqrt{5}}{2} x$, 可得 $\frac{b}{a}=\frac{\sqrt{5}}{2}$, 即 $\frac{c^{2}-a^{2}}{a^{2}}=\frac{5}{4}$, 可得 $\frac{c}{a}=\frac{3}{2}$, 解得 $a=2, b=\sqrt{5}$,
所求的双曲线方程为: $\frac{x^{2}}{4}-\frac{y^{2}}{5}=1$.
故选: B.
| 5 | 2010-2022_Math_I_MCQs |
|
2017 | (新课标ⅲ) | 设函数 $f(x)=\cos \left(x+\frac{\pi}{3}\right)$, 则下列结论错误的是 $(\quad)$
A. $f(x)$ 的一个周期为 $-2 \pi$
B. $y=f(x)$ 的图象关于直线 $x=\frac{8 \pi}{3}$ 对称
C. $f(x+\pi)$ 的一个零点为 $x=\frac{\pi}{6}$
D. $f(x)$ 在 $\left(\frac{\pi}{2}, \pi\right)$ 单调递减
| D | 解: $A$. 函数的周期为 $2 k \pi$, 当 $k=-1$ 时, 周期 $T=-2 \pi$, 故 $A$ 正确,
B. 当 $x=\frac{8 \pi}{3}$ 时, $\cos \left(x+\frac{\pi}{3}\right)=\cos \left(\frac{8 \pi}{3}+\frac{\pi}{3}\right)=\cos \frac{9 \pi}{3}=\cos 3 \pi=-1$ 为最小 值, 此时 $y=f(x)$ 的图象关于直线 $x=\frac{8 \pi}{3}$ 对称, 故 $B$ 正确,
C 当 $x=\frac{\pi}{6}$ 时, $f\left(\frac{\pi}{6}+\pi\right)=\cos \left(\frac{\pi}{6}+\pi+\frac{\pi}{3}\right)=\cos \frac{3 \pi}{2}=0$, 则 $f(x+\pi)$ 的一个 零点为 $x=\frac{\pi}{6}$, 故 $C$ 正确,
D. 当 $\frac{\pi}{2}<x<\pi$ 时, $\frac{5 \pi}{6}<x+\frac{\pi}{3}<\frac{4 \pi}{3}$, 此时函数 $f(x)$ 不是单调函数, 故 $D$ 错误,
故选: D.
| 5 | 2010-2022_Math_I_MCQs |
|
2017 | (新课标ⅲ) | 等差数列 $\left\{a_{n}\right\}$ 的首项为 1, 公差不为 0 . 若 $a_{2}, a_{3}, a_{6}$ 成等比数列, 则 $\left\{a_{n}\right\}$ 前 6 项的和为 $(\quad)$
A. -24
B. -3
C. 3
D. 8
| A | 解: $\because$ 等差数列 $\left\{a_{n}\right\}$ 的首项为 1, 公差不为 $0 . a_{2}, a_{3}, a_{6}$ 成等比数列, $\therefore \mathrm{a}_{3}^{2}=\mathrm{a}_{2} \cdot \mathrm{a}_{6}$
$\therefore\left(a_{1}+2 d\right)^{2}=\left(a_{1}+d\right) \quad\left(a_{1}+5 d\right)$, 且 $a_{1}=1, d \neq 0$,
解得 $d=-2$,
$\therefore\left\{a_{n}\right\}$ 前 6 项的和为 $S_{6}=6 a_{1}+\frac{6 \times 5}{2} d=6 \times 1+\frac{6 \times 5}{2} \times(-2)=-24$.
故选: A.
| 5 | 2010-2022_Math_I_MCQs |
|
2017 | (新课标ⅲ) | 已知椭圆 $C: \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1 \quad(a>b>0)$ 的左、右顶点分别为 $A_{1}, A_{2}$, 且以线段 $A_{1} A_{2}$ 为直径的圆与直线 $b x-a y+2 a b=0$ 相切, 则 $C$ 的离心率为
A. $\frac{\sqrt{6}}{3}$
B. $\frac{\sqrt{3}}{3}$
C. $\frac{\sqrt{2}}{3}$
D. $\frac{1}{3}$
| A | 解: 以线段 $A_{1} A_{2}$ 为直径的圆与直线 $b x-a y+2 a b=0$ 相切, $\therefore$ 原点到直线的距离 $\frac{2 a b}{\sqrt{a^{2}+b^{2}}}=a$, 化为: $a^{2}=3 b^{2}$.
$\therefore$ 椭圆 $\mathrm{C}$ 的离心率 $\mathrm{e}=\frac{\mathrm{c}}{\mathrm{a}}=\sqrt{1-\frac{\mathrm{b}^{2}}{\mathrm{a}^{2}}}=\frac{\sqrt{6}}{3}$.
故选: A.
| 5 | 2010-2022_Math_I_MCQs |
|
2017 | (新课标ⅲ) | 已知函数 $f(x)=x^{2}-2 x+a\left(e^{x-1}+e^{-x+1}\right)$ 有唯一零点, 则 $a=(\quad)$
A. $\quad-\frac{1}{2}$
B. $\frac{1}{3}$
C. $\frac{1}{2}$
D. 1
| C | 解: 因为 $f(x)=x^{2}-2 x+a\left(e^{x-1}+e^{-x+1}\right)=-1+(x-1)^{2}+a\left(e^{x-1}+\frac{1}{e^{x-1}}\right)$ $=0$,
所以函数 $f(x)$ 有唯一零点等价于方程 $1-(x-1)^{2}=a\left(e^{x-1}+\frac{1}{e^{x-1}}\right)$ 有唯一解, 等价于函数 $y=1-(x-1)^{2}$ 的图象与 $y=a\left(e^{x-1}+\frac{1}{e^{x-1}}\right)$ 的图象只有一个交点.
(1)当 $a=0$ 时, $f(x)=x^{2}-2 x \geqslant-1$, 此时有两个零点, 矛盾;
(2)当 $a<0$ 时, 由于 $y=1-(x-1)^{2}$ 在 $(-\infty, 1)$ 上递增、在 $(1,+\infty)$ 上递 减,
且 $y=a\left(e^{x-1}+\frac{1}{e^{x-1}}\right)$ 在 $(-\infty, 1)$ 上递增、在 $(1,+\infty)$ 上递减, 所以函数 $y=1-(x-1)^{2}$ 的图象的最高点为 $A(1,1), y=a\left(e^{x-1}+\frac{1}{e^{x-1}}\right)$ 的
图象的最高点为 $B(1,2 a)$,
由于 $2 a<0<1$, 此时函数 $y=1-(x-1)^{2}$ 的图象与 $y=a\left(e^{x-1}+\frac{1}{e^{x-1}}\right)$ 的图象 有两个交点,矛盾;
(3)当 $a>0$ 时, 由于 $y=1-(x-1)^{2}$ 在 $(-\infty, 1)$ 上递增、在 $(1,+\infty)$ 上递 减,
且 $y=a\left(e^{x-1}+\frac{1}{e^{x-1}}\right)$ 在 $(-\infty, 1)$ 上递减、在 $(1,+\infty)$ 上递增,
所以函数 $y=1-(x-1)^{2}$ 的图象的最高点为 $A(1,1), y=a\left(e^{x-1}+\frac{1}{e^{x-1}}\right)$ 的
图象的最低点为 $B(1,2 a)$,
由题可知点 $A$ 与点 $B$ 重合时满足条件, 即 $2 a=1$, 即 $a=\frac{1}{2}$, 符合条件;
综上所述, $a=\frac{1}{2}$,
故选: C.
| 5 | 2010-2022_Math_I_MCQs |
|
2018 | (新课标ⅰ) | 设 $z=\frac{1-i}{1+i}+2 i$, 则 $|z|=(\quad)$
A. 0
B. $\frac{1}{2}$
C. 1
D. $\sqrt{2}$
| C | 解 $z=\frac{1-i}{1+i}+2 i=\frac{(1-i)(1-i)}{(1-i)(1+i)}+2 i=-i+2 i=i$,
则 $|z|=1$.
故选: C.
| 5 | 2010-2022_Math_I_MCQs |
|
2018 | (新课标ⅰ) | 已知集合 $A=\left\{x \mid x^{2}-x-2>0\right\}$, 则 $\left.C_{R} A=( \quad\right)$
A. $\{x \mid-1<x<2\}$
B. $\{x \mid-1 \leqslant x \leqslant 2\}$
C. $\{x \mid x<-1\} \cup\{x \mid x>2\}$
D. $\{x \mid x \leqslant-1\}$
$U\{x \mid x \geqslant 2\}$
| B | 解:集合 $A=\left\{x \mid x^{2}-x-2>0\right\}$,
可得 $A=\{x \mid x<-1$ 或 $x>2\}$, 则: $C_{R} A=\{x \mid-1 \leqslant x \leqslant 2\}$.
故选: B.
| 5 | 2010-2022_Math_I_MCQs |
|
2018 | (新课标ⅰ) | 记 $S_{n}$ 为等差数列 $\left\{a_{n}\right\}$ 的前 $n$ 项和. 若 $3 S_{3}=S_{2}+S_{4}, a_{1}=2$, 则 $a_{5}=(\quad)$
A. -12
B. -10
C. 10
D. 12
| B | 解: $\because S_{n}$ 为等差数列 $\left\{a_{n}\right\}$ 的前 $n$ 项和, $3 S_{3}=S_{2}+S_{4}, a_{1}=2$,
$\therefore 3 \times\left(3 \mathrm{a}_{1}+\frac{3 \times 2}{2} \mathrm{~d}\right)=\mathrm{a}_{1}+\mathrm{a}_{1}+d+4 \mathrm{a}_{1}+\frac{4 \times 3}{2} \mathrm{~d}$,
把 $a_{1}=2$, 代入得 $d=-3$
$\therefore a_{5}=2+4 \times(-3)=-10$.
故选: B.
| 5 | 2010-2022_Math_I_MCQs |
|
2018 | (新课标ⅰ) | 设函数 $f(x)=x^{3}+(a-1) x^{2}+a x$. 若 $f(x)$ 为奇函数, 则曲线 $y=f($ $x$ ) 在点 $(0,0)$ 处的切线方程为 ( )
A. $y=-2 x$
B. $y=-x$
C. $y=2 x$
D. $y=x$
| D | 解: 函数 $f(x)=x^{3}+(a-1) x^{2}+a x$, 若 $f(x)$ 为奇函数,
可得 $a=1$, 所以函数 $f(x)=x^{3}+x$, 可得 $f^{\prime}(x)=3 x^{2}+1$,
曲线 $y=f(x)$ 在点 $(0,0)$ 处的切线的斜率为: 1 ,
则曲线 $y=f(x)$ 在点 $(0,0)$ 处的切线方程为: $y=x$.
故选:D.
| 5 | 2010-2022_Math_I_MCQs |
|
2018 | (新课标ⅰ) | 在 $\triangle A B C$ 中, $A D$ 为 $B C$ 边上的中线, $E$ 为 $A D$ 的中点, 则 $\overrightarrow{E B}=(\quad)$
A. $\frac{3}{4} \overrightarrow{\mathrm{AB}}-\frac{1}{4} \overrightarrow{\mathrm{AC}}$
B. $\frac{1}{4} \overrightarrow{\mathrm{AB}}-\frac{3}{4} \overrightarrow{\mathrm{AC}}$
C. $\frac{3}{4} \overrightarrow{\mathrm{AB}}+\frac{1}{4} \overrightarrow{\mathrm{AC}}$
D. $\frac{1}{4} \overrightarrow{\mathrm{AB}}+\frac{3}{4} \overrightarrow{\mathrm{AC}}$
| A | 解: 在 $\triangle A B C$ 中, $A D$ 为 $B C$ 边上的中线, $E$ 为 $A D$ 的中点,
$\overrightarrow{\mathrm{EB}}=\overrightarrow{\mathrm{AB}}-\overrightarrow{\mathrm{AE}}=\overrightarrow{\mathrm{AB}}-\frac{1}{2} \overrightarrow{\mathrm{AD}}$
$=\overrightarrow{\mathrm{AB}}-\frac{1}{2} \times \frac{1}{2}(\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{AC}})$
$=\frac{3}{4} \overrightarrow{\mathrm{AB}}-\frac{1}{4} \overrightarrow{\mathrm{AC}}$ 故选: A.
| 5 | 2010-2022_Math_I_MCQs |
|
2018 | (新课标ⅰ) | 设抛物线 $C: y^{2}=4 x$ 的焦点为 $F$, 过点 $(-2,0)$ 且斜率为 $\frac{2}{3}$ 的直线与 $C$ 交于 $M, N$ 两点, 则 $\overrightarrow{F M} \bullet \overrightarrow{F N}=(\quad)$
A. 5
B. 6
C. 7
D. 8
| D | 解:抛物线 $C: y^{2}=4 x$ 的焦点为 $F(1,0)$, 过点 $(-2,0)$ 且斜率为 $\frac{2}{3}$ 的直线为: $3 y=2 x+4$,
联立直线与抛物线 $C: y^{2}=4 x$, 消去 $x$ 可得: $y^{2}-6 y+8=0$ ,
解得 $y_{1}=2, y_{2}=4$, 不妨 $M(1,2), N(4,4), \overrightarrow{F M}=(0,2), \overrightarrow{F N}=(3,4)$. 则 $\overrightarrow{F M} \bullet \overrightarrow{F N}=(0,2) \bullet(3,4)=8$.
故选: D.
| 5 | 2010-2022_Math_I_MCQs |
|
2018 | (新课标ⅰ) | 已知双曲线 $C: \frac{x^{2}}{3}-y^{2}=1, O$ 为坐标原点, $F$ 为 $C$ 的右焦点, 过 $F$ 的直线与 $C$ 的两条渐近线的交点分别为 $M, N$. 若 $\triangle O M N$ 为直角三角形, 则 $|\mathrm{MN}|=(\quad)$
A. $\frac{3}{2}$
B. 3
C. $2 \sqrt{3}$
D. 4
| B | 解: 双曲线 $c: \frac{x^{2}}{3}-y^{2}=1$ 的渐近线方程为: $y= \pm \frac{\sqrt{3}}{3} x$, 渐近线的夹角 为: $60^{\circ}$, 不妨设过 $F(2,0)$ 的直线为: $y=\sqrt{3}(x-2)$, 则: $\left\{\begin{array}{l}y=\frac{\sqrt{3}}{3} x \\ y=\sqrt{3}(x-2)\end{array}\right.$ 解得 $M\left(\frac{3}{2},-\frac{\sqrt{3}}{2}\right)$,
$\left\{\begin{array}{l}y=\frac{\sqrt{3}}{3} x \\ y=\sqrt{3}(x-2)\end{array}\right.$ 解得: $N(3, \sqrt{3})$,
则 $|M N|=\sqrt{\left(3-\frac{3}{2}\right)^{2}+\left(\sqrt{3}+\frac{\sqrt{3}}{2}\right)^{2}}=3$.
故选:B.
| 5 | 2010-2022_Math_I_MCQs |
|
2018 | (新课标ⅱ) | 1. (5 分 $) \frac{1+2 i}{1-2 i}=(\quad)$
A. $-\frac{4}{5}-\frac{3}{5} i$
B. $-\frac{4}{5}+\frac{3}{5} i$
C. $-\frac{3}{5}-\frac{4}{5} i$
D. $-\frac{3}{5}+\frac{4}{5} i$
| D | 解: $\frac{1+2 i}{1-2 i}=\frac{(1+2 i)(1+2 i)}{(1-2 i)(1+2 i)}=-\frac{3}{5}+\frac{4}{5} i$.
故选: D.
| 5 | 2010-2022_Math_I_MCQs |
|
2018 | (新课标ⅱ) | 已知集合 $A=\left\{(x, y) \mid x^{2}+y^{2} \leqslant 3, x \in Z, y \in Z\right\}$, 则 $A$ 中元素的个数为
A. 9
B. 8
C. 5
D. 4
| A | 解: 当 $x=-1$ 时, $y^{2} \leqslant 2$, 得 $y=-1,0,1$,
当 $x=0$ 时, $y^{2} \leqslant 3$, 得 $y=-1,0,1$,
当 $x=1$ 时, $y^{2} \leqslant 2$, 得 $y=-1,0,1$,
即集合 $A$ 中元素有 9 个, 故选:A.
| 5 | 2010-2022_Math_I_MCQs |
|
2018 | (新课标ⅱ) | 已知向量 $\vec{a}, \vec{b}$ 满足 $|\vec{a}|=1, \vec{a} \cdot \vec{b}=-1$, 则 $\vec{a} \bullet(2 \vec{a}-\vec{b})=(\quad )$
A. 4
B. 3
C. 2
D. 0
| B | 解 向量 $\vec{a}, \vec{b}$ 满足 $|\vec{a}|=1, \vec{a} \cdot \vec{b}=-1$, 则 $\vec{a} \cdot(2 \vec{a}-\vec{b})=2 \vec{a}-\vec{a} \cdot \vec{b}=2+1=3$
故选: B.
| 5 | 2010-2022_Math_I_MCQs |
|
2018 | (新课标ⅱ) | 双曲线 $\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1(a>0, b>0)$ 的离心率为 $\sqrt{3}$, 则其渐近线方程为 $(\quad)$
A. $y= \pm \sqrt{2} x$
B. $y= \pm \sqrt{3} x$
C. $y= \pm \frac{\sqrt{2}}{2} x$
D. $y= \pm \frac{\sqrt{3}}{2} \mathrm{x}$
| A | 解: $\because$ 双曲线的离心率为 $e=\frac{c}{a}=\sqrt{3}$,
则 $\frac{b}{a}=\sqrt{\frac{b^{2}}{a^{2}}}=\sqrt{\frac{c^{2}-a^{2}}{a^{2}}}=\sqrt{\left(\frac{c}{a}\right)^{2}-1}=\sqrt{3-1}=\sqrt{2}$,
即双曲线的渐近线方程为 $y= \pm \frac{b}{a} x= \pm \sqrt{2} x$,
故选:A.
| 5 | 2010-2022_Math_I_MCQs |
|
2018 | (新课标ⅱ) | 在 $\triangle A B C$ 中, $\cos \frac{C}{2}=\frac{\sqrt{5}}{5}, B C=1, A C=5$, 则 $A B=( )$
A. $4 \sqrt{2}$
B. $\sqrt{30}$
C. $\sqrt{29}$
D. $2 \sqrt{5}$
| A | 解:在 $\triangle \mathrm{ABC}$ 中, $\cos \frac{\mathrm{C}}{2}=\frac{\sqrt{5}}{5}, \cos \mathrm{C}=2 \times\left(\frac{\sqrt{5}}{5}\right)^{2}-1=-\frac{3}{5}$,
$B C=1, A C=5$, 则 $A B=\sqrt{B C^{2}+A C^{2}-2 B C \cdot A C \cos C}=\sqrt{1+25+2 \times 1 \times 5 \times \frac{3}{5}}=\sqrt{32}=4 \sqrt{2}$.
故选: A.
| 5 | 2010-2022_Math_I_MCQs |
|
2018 | (新课标ⅱ) | 我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果. 哥德巴赫猜想是“每个大于 2 的偶数可以表示为两个素数的和”, 如 $30=7+23$. 在不超过 30 的素数中, 随机选取两个不同的数, 其和等于 30 的概率是 $(\quad)$
A. $\frac{1}{12}$
B. $\frac{1}{14}$
C. $\frac{1}{15}$
D. $\frac{1}{18}$
| C | 解: 在不超过 30 的素数中有, $2,3,5,7,11,13,17,19,23,29$ 共 10 个,
从中选 2 个不同的数有 $C_{10}^{2}=45$ 种,
和等于 30 的有 $(7,23)$, $(11,19),(13,17)$, 共 3 种,
则对应的概率 $P=\frac{3}{45}=\frac{1}{15}$,
故选: C.
| 5 | 2010-2022_Math_I_MCQs |
|
2018 | (新课标ⅱ) | 若 $f(x)=\cos x-\sin x$ 在 $[-a, a]$ 是减函数, 则 $a$ 的最大值是 $(\quad)$
A. $\frac{\pi}{4}$
B. $\frac{\pi}{2}$
C. $\frac{3 \pi}{4}$
D. $\pi$
| A | 解: $f(x)=\cos x-\sin x=-(\sin x-\cos x)=-\sqrt{2} \sin \left(x-\frac{\pi}{4}\right)$,
由 $-\frac{\pi}{2}+2 k \pi \leqslant x-\frac{\pi}{4} \leqslant \frac{\pi}{2}+2 k \pi, k \in Z$,
得 $-\frac{\pi}{4}+2 k \pi \leqslant x \leqslant \frac{3}{4} \pi+2 k \pi, k \in Z$,
取 $\mathrm{k}=0$, 得 $\mathrm{f}(\mathrm{x})$ 的一个减区间为 $\left[-\frac{\pi}{4}, \frac{3}{4} \pi\right]$,
由 $f(x)$ 在 $[-a, a]$ 是减函数, 得 $\left\{\begin{array}{l}-a \geqslant-\frac{\pi}{4} \\ a \leqslant \frac{3 \pi}{4}\end{array}, \quad \therefore a \leqslant \frac{\pi}{4}\right.$.
则 $a$ 的最大值是 $\frac{\pi}{4}$.
故选: A.
| 5 | 2010-2022_Math_I_MCQs |
|
2018 | (新课标ⅱ) | 已知 $f(x)$ 是定义域为 $(-\infty,+\infty)$ 的奇函数, 满足 $f(1-x)=f$ $(1+x)$, 若 $f(1)=2$, 则 $f(1)+f(2)+f(3)+\ldots+f(50)=(\quad)$
A. -50
B. 0
C. 2
D. 50
| C | 解: $\because f(x)$ 是奇函数, 且 $f(1-x)=f(1+x)$,
$\therefore f(1-x)=f(1+x)=-f(x-1), f(0)=0$,
则 $f(x+2)=-f(x)$, 则 $f(x+4)=-f(x+2)=f(x)$,
即函数 $f(x)$ 是周期为 4 的周期函数,
$\because f(1)=2$,
$\therefore f(2)=f(0)=0, f(3)=f(1-2)=f(-1)=-f(1)=-2$,
$f(4)=f(0)=0$
则 $f(1)+f(2)+f(3)+f(4)=2+0-2+0=0$,
则 $f(1)+f(2)+f(3)+\ldots+f(50)=12[f(1)+f(2)+f(3)+f(4)]+f(49)$
$+f(50)$
$=f(1)+f(2)=2+0=2$, 故选:C.
| 5 | 2010-2022_Math_I_MCQs |
|
2018 | (新课标ⅲ) | 已知集合 $A=\{x \mid x-1 \geqslant 0\}, B=\{0,1,2\}$, 则 $A \cap B=( \quad)$
A. $\{0\}$
B. $\{1\}$
C. $\{1,2\}$
D. $\{0,1,2\}$
| C | 解: $\because A=\{x \mid x-1 \geqslant 0\}=\{x \mid x \geqslant 1\}, B=\{0,1,2\}$,
$\therefore A \cap B=\{x \mid x \geqslant 1\} \cap\{0,1,2\}=\{1,2\}$.
故选: C.
| 5 | 2010-2022_Math_I_MCQs |
|
2018 | (新课标ⅲ) | 2. $(5$ 分 $)(1+i)(2-i)=(\quad)$
A. $-3-i$
B. $-3+i$
C. $3-i$
D. $3+i$
| D | 解: $(1+i)(2-i)=3+i$. 故选: D.
| 5 | 2010-2022_Math_I_MCQs |
|
2018 | (新课标ⅲ) | 若 $\sin a=\frac{1}{3}$, 则 $\cos 2 a=(\quad)$
A. $\frac{8}{9}$
B. $\frac{7}{9}$
C. $-\frac{7}{9}$
D. $-\frac{8}{9}$
| B | 解: $\because \sin a=\frac{1}{3}$,
$\therefore \cos 2 a=1-2 \sin ^{2} a=1-2 \times \frac{1}{9}=\frac{7}{9}$.
故选: $B$.
| 5 | 2010-2022_Math_I_MCQs |
|
2018 | (新课标ⅲ) | $\left(x^{2}+\frac{2}{x}\right){ }^{5}$ 的展开式中 $x^{4}$ 的系数为 $(\quad)$
A. 10
B. 20
C. 40
D. 80
| C | 解:由二项式定理得 $\left(x^{2}+\frac{2}{x}\right)^{5}$ 的展开式的通项为:
$$
T_{r+1}=C_{5}^{r}\left(x^{2}\right)^{5-r}\left(\frac{2}{x}\right)^{r}=2^{r} C_{5}^{r} x^{10-3 r}
$$
由 $10-3 r=4$, 解得 $r=2$,
$\therefore\left(\mathrm{x}^{2}+\frac{2}{\mathrm{x}}\right)^{5}$ 的展开式中 $\mathrm{x}^{4}$ 的系数为 $2^{2} \mathrm{C}_{5}^{2}=40$.
故选: C.
| 5 | 2010-2022_Math_I_MCQs |
|
2018 | (新课标ⅲ) | 直线 $x+y+2=0$ 分别与 $x$ 轴, $y$ 轴交于 $A$, B 两点, 点 $P$ 在圆 $(x-2)$ ${ }^{2}+y^{2}=2$ 上,则 $\triangle A B P$ 面积的取值范围是 $(\quad)$
A. $[2,6]$
B. $[4,8]$
C. $[\sqrt{2}, 3 \sqrt{2}]$
D. $[2 \sqrt{2}, 3 \sqrt{2}]$
| A | 解: $\because$ 直线 $x+y+2=0$ 分别与 $x$ 轴, $y$ 轴交于 $A, B$ 两点, $\therefore$ 令 $\mathrm{x}=0$, 得 $\mathrm{y}=-2$, 令 $\mathrm{y}=0$, 得 $\mathrm{x}=-2$,
$\therefore A(-2,0), B(0,-2),|A B|=\sqrt{4+4}=2 \sqrt{2}$,
$\because$ 点 $P$ 在圆 $(x-2)^{2}+y^{2}=2$ 上, $\therefore$ 设 $P(2+\sqrt{2} \cos \theta, \sqrt{2} \sin \theta)$,
$\therefore$ 点 $\mathrm{P}$ 到直线 $\mathrm{x}+\mathrm{y}+2=0$ 的距离: $\mathrm{d}=\frac{|2+\sqrt{2} \cos \theta+\sqrt{2} \sin \theta+2|}{\sqrt{2}}=\frac{\left|2 \sin \left(\theta+\frac{\pi}{4}\right)+4\right|}{\sqrt{2}}$,
$\because \sin \left(\theta+\frac{\pi}{4}\right) \in[-1,1], \quad \therefore d=\frac{\left|2 \sin \left(\theta+\frac{\pi}{4}\right)+4\right|}{\sqrt{2}} \in[\sqrt{2}, 3 \sqrt{2}]$,
$\therefore \triangle \mathrm{ABP}$ 面积的取值范围是:
$\left[\frac{1}{2} \times 2 \sqrt{2} \times \sqrt{2}, \frac{1}{2} \times 2 \sqrt{2} \times 3 \sqrt{2}\right]=[2,6]$.
故选: $A$.
| 5 | 2010-2022_Math_I_MCQs |
|
2018 | (新课标ⅲ) | 某群体中的每位成员使用移动支付的概率都为 $\mathrm{p}$, 各成员的支付方式 相互独立. 设 $\mathrm{X}$ 为该群体的 10 位成员中使用移动支付的人数, $D X=2.4, P$ $(x=4)<P(X=6)$, 则 $p=(\quad)$
A. 0.7
B. 0.6
C. 0.4
D. 0.3
| B | 解:某群体中的每位成员使用移动支付的概率都为 $\mathrm{p}$, 看做是独立重复 事件,满足 $X \sim B \quad(10, \mathrm{p})$,
$P(x=4)<P(X=6)$, 可得 $C_{10}^{4} p^{4}(1-p)^{6}<c_{10}^{6} p^{6}(1-p)^{4}$, 可得 $1-2 p<0$. 即 $p>\frac{1}{2}$
因为 $D X=2.4$, 可得 $10 p(1-p)=2.4$, 解得 $p=0.6$ 或 $p=0.4$ (舍去).
故选: $B$.
| 5 | 2010-2022_Math_I_MCQs |
|
2018 | (新课标ⅲ) | $\triangle A B C$ 的内角 A, B, C 的对边分别为 $a, b, C$. 若 $\triangle A B C$ 的面积为 $\frac{a^{2}+b^{2}-c^{2}}{4}$, 则 $\mathrm{C}=(\quad)$
A. $\frac{\pi}{2}$
B. $\frac{\pi}{3}$
C. $\frac{\pi}{4}$
D. $\frac{\pi}{6}$
| C | 解: $\because \triangle A B C$ 的内角 $A, B, C$ 的对边分别为 $a, b, c$.
$\triangle A B C$ 的面积为 $\frac{a^{2}+b^{2}-c^{2}}{4}$,
$\therefore S_{\triangle A B C}=\frac{1}{2} a b \sin C=\frac{a^{2}+b^{2}-c^{2}}{4}$ $\therefore \sin \mathrm{C}=\frac{\mathrm{a}^{2}+\mathrm{b}^{2}-\mathrm{c}^{2}}{2 \mathrm{ab}}=\cos \mathrm{C}$,
$\because 0<\mathrm{C}<\pi, \quad \therefore \mathrm{C}=\frac{\pi}{4}$.
故选: C.
| 5 | 2010-2022_Math_I_MCQs |
|
2018 | (新课标ⅲ) | 设 $F_{1}, F_{2}$ 是双曲线 $C: \frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1(a>0, b>0)$ 的左, 右焦点, $O$ 是坐标原点. 过 $F_{2}$ 作 $C$ 的一条渐近线的垂线, 垂足为 $P$, 若 $\left|P F_{1}\right|=\sqrt{6}|O P|$, 则 $C$ 的离心率为 $(\quad)$
A. $\sqrt{5}$
B. 2
C. $\sqrt{3}$
D. $\sqrt{2}$
| C | 解:双曲线 $C: \frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1 \quad(a>0 . b>0)$ 的一条渐近线方程为 $y=\frac{b}{a} x$, $\therefore$ 点 $\mathrm{F}_{2}$ 到渐近线的距离 $\mathrm{d}=\frac{\mathrm{bc}}{\sqrt{\mathrm{a}^{2}+\mathrm{b}^{2}}}=\mathrm{b}$, 即 $\left|P F_{2}\right|=b$,
$\therefore|\mathrm{OP}|=\sqrt{\left|O \mathrm{~F}_{2}\right|^{2}-\left|\mathrm{PF}_{2}\right|^{2}}=\sqrt{c^{2}-\mathrm{b}^{2}}=\mathrm{a}, \quad \cos \angle \mathrm{PF} \mathrm{F}_{2} \mathrm{O}=\frac{\mathrm{b}}{\mathrm{c}}$,
$\because\left|\mathrm{PF}_{1}\right|=\sqrt{6}|\mathrm{OP}|$
$\therefore\left|P F_{1}\right|=\sqrt{6} a$ 在三角形 $F_{1} P F_{2}$ 中, 由余弦定理可得 $\left|P F_{1}\right|^{2}=\left|P F_{2}\right|^{2}+\left|F_{1} F_{2}\right|^{2}-2\left|P F_{2}\right| \cdot\left|F_{1} F_{2}\right| C O S \angle$ $\mathrm{PF}_{2} \mathrm{O}$
$\therefore 6 \mathrm{a}^{2}=\mathrm{b}^{2}+4 c^{2}-2 \times b \times 2 c \times \frac{b}{c}=4 c^{2}-3 b^{2}=4 c^{2}-3 \quad\left(c^{2}-a^{2}\right)$,
即 $3 a^{2}=c^{2}$,
即 $\sqrt{3} a=c$,
$\therefore \mathrm{e}=\frac{\mathrm{c}}{\mathrm{a}}=\sqrt{3}$,
故选: C.
| 5 | 2010-2022_Math_I_MCQs |
|
2018 | (新课标ⅲ) | 设 $a=\log _{0.2} 0.3, b=\log _{2} 0.3$, 则 $(\quad)$
A. $a+b<a b<0$
B. $a b<a+b<0$
C. $a+b<0<a b$
D. $a b<0<a+b$
| B | 解: $\because \mathrm{a}=\log _{0.2} 0.3=\frac{1 \mathrm{~g} 0.3}{-\lg 5}, \mathrm{~b}=\log _{2} 0.3=\frac{\lg 0.3}{1 \mathrm{~g} 2}$,
$\therefore \mathrm{a}+\mathrm{b}=\frac{\lg 0.3}{\lg 2}-\frac{\lg 0.3}{\lg 5}=\frac{\lg 0.3(\lg 5-\lg 2)}{\lg 2 \lg 5}=\frac{\lg 0.3 \lg \frac{5}{2}}{\lg 2 \lg 5}$,
$\mathrm{ab}=-\frac{\lg 0.3}{\lg 2} \cdot \frac{\lg 0.3}{\lg 5}=\frac{\lg 0.3 \cdot 1 \mathrm{~g} \frac{10}{3}}{\lg 2 \lg 5}$,
$\because \lg \frac{10}{3}>\lg \frac{5}{2}, \frac{\lg 0.3}{\lg 2 \lg 5}<0$,
$\therefore \mathrm{ab}<\mathrm{a}+\mathrm{b}<0$.
故选: B.
| 5 | 2010-2022_Math_I_MCQs |
|
2019 | (新课标ⅰ) | 1.已知集合 $M=\{x \mid-4<x<2\}, N=\left\{x \mid x^{2}-x-6<0\right\}$, 则 $M \cap N=$
A. $\{x \mid-4<x<3\}$
B. $\{x \mid-4<x<-2\}$
C. $\{x \mid-2<x<2\}$
D.
$\{x \mid 2<x<3\}$
| C | 【详解】由题意得, $M=\{x \mid-4<x<2\}, N=\{x \mid-2<x<3\}$, 则
$M \cap N=\{x \mid-2<x<2\}$. 故选 C.
| 5 | 2010-2022_Math_I_MCQs |
|
2019 | (新课标ⅰ) | 2. 设复数 $z$ 满足 $|z-\mathrm{i}|=1, z$ 在复平面内对应的点为 $(x, y)$, 则
A. $(x+1)^{2}+y^{2}=1$
B. $(x-1)^{2}+y^{2}=1$
C. $x^{2}+(y-1)^{2}=1$
D.
$x^{2}+(y+1)^{2}=1$
| C | 【详解】 $z=x+y i, z-i==x+(y-1) i,|z-i|=\sqrt{x^{2}+(y-1)^{2}}=1$, 则 $x^{2}+(y-1)^{2}=1$. 故选 C.
| 5 | 2010-2022_Math_I_MCQs |
|
2019 | (新课标ⅰ) | 3.已知 $a=\log _{2} 0.2, b=2^{0.2}, c=0.2^{0.3}$ ,则
A. $a<b<c$
B. $a<c<b$
C. $c<a<b$
D.
$b<c<a$
| B | 【详 解 】 $a=\log _{2} 0.2<\log _{2} 1=0, \quad b=2^{0.2}>2^{0}=1, \quad 0<0.2^{0.3}<0.2^{0}=1$, 则 $0<c<1, a<c<b$. 故选 B.
| 5 | 2010-2022_Math_I_MCQs |